Introduction
Fractional calculus has recently been applied to modern engineering advances, mechanics, physics, biology, bioengineering, etc, introducing non-local derivatives. Leibniz [1] originated fractional calculus, with Liouville [2], Riemann [3], and other famous mathematicians. Samko, et al. [4], Poldubny [5]. Oldham, et al. [6], and Miller, et al. [7] are typical sources informing about fractional calculus. Fractional derivative models have been introduced, to describe the deformation of various models in mechanics. Bagley, et al. [8,9], Atanackovic [10], Mainardi [11]. introduced fractional viscoelastic models, trying to simulate their experiments. Various studies in fractional differential equations are presented in [12-15]. Lazopoulos [13] turning the interest from time to space, just to discuss non-homogeneous materials with possible voids, etc, proposed a model with fractional space derivatives and has presented a series of papers establishing the fractional deformation of the materials. has presented wave propagation in viscoelastic materials with fractional calculus. Noll's axiom of local action, Truesdell [14] is not valid anymore. Hence, the stress at a point does not depend only upon the (local) strain at that point, but on the strain of a region around the point. That postulate has been introduced by Eringen [15], indicating that in micro and nano materials the stress at a point depends on the deformation of a region around that point contrary, to the conventional elasticity based upon Noll’s axiom.
It is evident that fractional derivatives not only abolish the local character of the conventional derivatives but also fail to be derivatives satisfying the prerequisites of Differential Topology, Chillingworth [16], which are: a. Linearity, b. Leibniz rule c. Chain rule. Lazopoulos [17] trying to fill that gap proposed the Λ-fractional analysis with the Λ-fractional derivative satisfying all the necessary postulates of differential topology for real mathematical derivatives. Λ-fractional analysis has been applied to mechanics, differential equations, geometry, physics, etc. Lazopoulos [18-25]. However, although Λ-fractional analysis responds to the need for global considerations of a problem, what has been overlooked is the global stability analysis of those problems. Indeed, the considered variational procedures are local, whereas all the other factors of the problems are global. Therefore, globally stable solutions are considered with discontinuities introduced by Weierstrass-Erdman corner conditions.
The fractional calculus
The fractional integrals are defined by,
For a fractional dimension 0 < γ ≤ 1. Eq.(1) defines the left and Eq.(2) the right fractional integral, whereas γ is the order of fractional integrals and Γ(γ) Euler’s Gamma function. Although many fractional derivatives exist, Riemann-Liouville fractional derivative (R-L) will be considered, defined by:
That is the left R-L derivative, whereas the right Riemann-Liouville’s fractional derivative (R-L) is defined by:
The fractional integrals and derivatives are related by the expression,
Since fractional calculus, based upon fractional derivatives, are not sufficient to generate differentials, Lazopoulos [17] proposed Λ-Fractional analysis, just to bridge the inability of fractional derivatives to generate differentials. The Λ-fractional analysis proposes a dual space, the Λ-fractional space, where everything behaves conventionally. Therefore the derivatives in the proposed Λ-space are local and differentials may be generated. Further differential geometry is established with variational procedures and field theorems. In addition, Λ-fractional analysis can generate theorems corresponding to the existence and uniqueness of the fractional differential equations. The Λ-fractional derivative (Λ-FD) is defined by:
Recalling, Eq. (3), the Λ-FD is defined by,
The dual Λ-fractional space to the initial space is defined by (X, F(X)) coordinates, with,
Thus, the Λ-FD is a local derivative, in the dual Λ-fractional space (X, F(X)). Hence, the conventional mathematical analysis applied in that space acquires the demanded accuracy. Consequently, differential geometry exists in that dual space. Further, no question arises concerning the accuracy of various other important mathematical tools used in applications like variational procedures and field theorems, existence and uniqueness theorems of differential equations. Further, the various results may be transferred into the initial space, that is the dual to the dual of the initial space, following the relation,
Implementation of Λ-fractional analysis
For a better understanding of the proposed Λ-fractional analysis, the fractional tangent space of the curve
f(x)=x5 (10)
is presented. In fact there exist two spaces, the initial space (x, f(x)) and the Λ-fractional space (X, F(X)). According to Eq. (8)
The fractional Λ-space is formulated if x is substituted through Eq.(8a). Indeed,
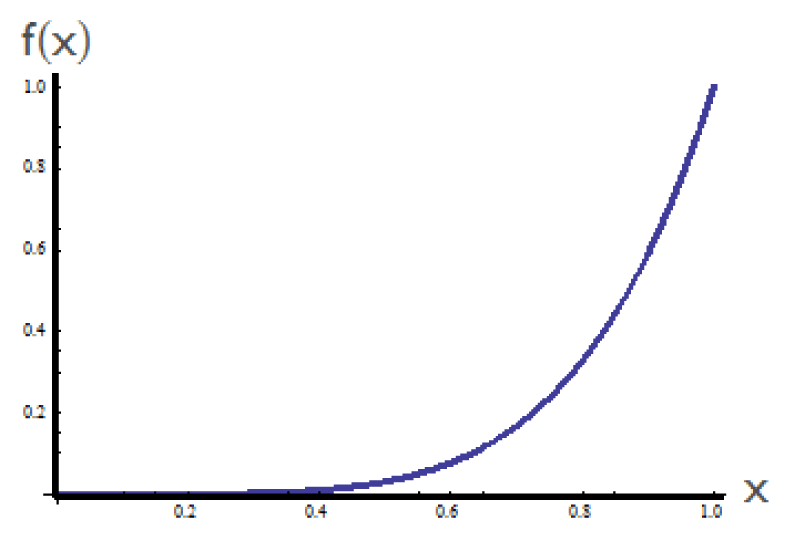
The initial space concerning the curve of Eq. (10) is shown in Figure (1).
Figure 1: The function
f(x)=x5.
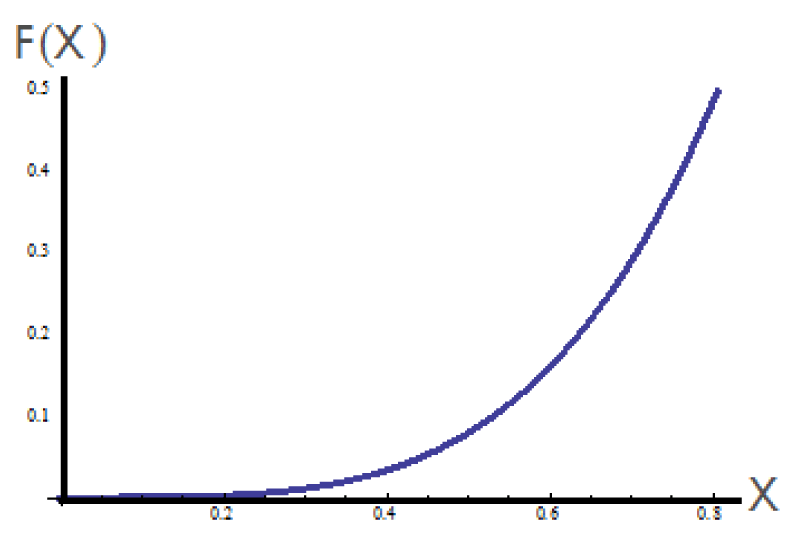
Further, the configuration of that curve in the Λ-fractional space is shown in Figure (2).
Figure 2: The Λ-fractional space with γ = 0.6.
Further, the Λ-fractional derivative is defined by,
It is again pointed out that the Λ-fractional derivatives are local (common) in the Λ-fractional space. Hence, the Λ-FD in the fractional Λ-space behaves according to the conventional derivative. Just to illustrate the point, the tangent space in the fractional Λ-space is shown in Figure 3 at the point X = 0.7.
Figure 3: The configuration of the curve
f(x) = x5 in the fractional Λ-space with its tangent space at
Χ = 0.7.
The tangent space of the curve F(X) in the Λ-space at the point X = 0.7 is defined by the equation:
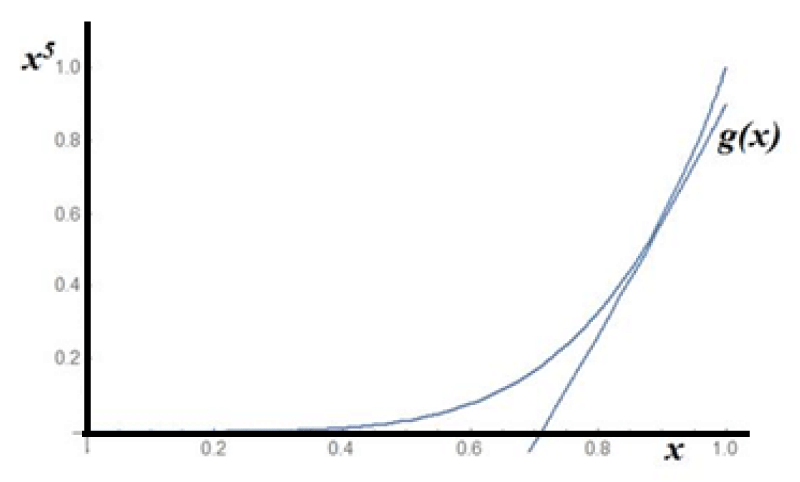
Taking into consideration the correspondence between x and X, Eq. (8), the point X0 = 0.7 for γ = 0.6 corresponds to the point x0 = 0.9. Transferring the tangent line into the initial space, the corresponding tangent curve is defined by (Figure 4),
Figure 4: The initial curve with the transferred tangent curve
g(x) from the Λ-space.
With X defined by
.
It should be taken into consideration that no geometry may be transferred into the initial space. Only functions from the Λ-space may be transferred into the initial one.
The Λ-fractional Euler-Lagrange equation
Transferring the problem from the initial space (x, y(x)) to the (dual) Λ-fractional space the corresponding parameters of the problem (X, Y(X), Y (X)) are defined through,
and
The extermination of the functional in the Λ- fractional space is expressed by,
with some corresponding boundary conditions.
The extremal equation is defined by,
With the boundary conditions. In conventional equilibrium problems one has to solve the above extremal problem, just to complete the solution. That happens because the local criterion of stability is adopted, with continuous derivatives. However, in the present Λ-fractional analysis global criteria should only be considered, since everything concerning fractional calculus is global. In fact solutions of the extremal Eq. (19) are adopted with n on-continuous derivatives. In fact, the Weierstrass-Erdman corner conditions, [26], should additionally be satisfied with,
That is imposed for every variational problem in fractional calculus since only global minimization is considered. Further, the results should be transferred into the initial space. In that space, only functions may be transferred, not derivatives, since fractional derivatives do not exist in the initial space but only functions. In fact, the function Y(X) defined as extremal of the variational problem in the Λ-fractional space should be transferred into the initial space with the help of the Eqs. (8). Indeed,
Further, transferring into the initial space should be effected using Eq. (9).
The Λ-fractional refraction of light
The constant velocity of light in a medium I is υ1 and in medium II is υ2 Medium I is separated from medium II by the line y = 0. Derive the law of refraction of a light ray going from point a = (x1, y1) in a medium I, to point b = (x2, y2) in medium II if we know that the light ray transverses this path in the shortest time interval.
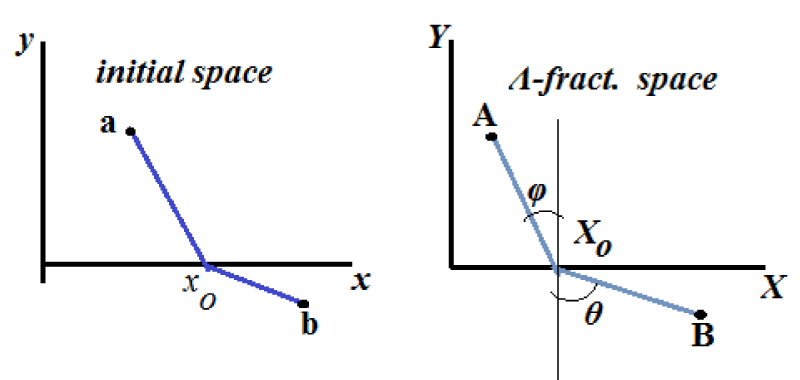
The points a and b in the initial space, correspond to the points A = (X1, Y1) and B = (X2, Y2) in the Λ-fractional space, Figure 5.
Figure 5: The Λ-fractional light refraction problem.
If γ is the fractional order corresponding to various material non-homogeneous distributions, the Λ-fractional space is defined by,
corresponding to the (x, y) points of the initial space.
The light Λ-fractional light refraction problem is formulated in the Λ-fractional space and reduces to minimization of the integral,
The minimization of the integral is effected with the consideration simultaneously of both the Euler-Lagrange equation and the corner conditions.
The solution is defined through the angles φ and θ with the relation see [26], p. 159, where, v1 and v2 are the light velocities in a medium I and medium II respectively. It is proven that the minimum time for the light traveling from point A to point B is defined for the zigzag straight line AXoB,
That relation defines the point Xo where the light beam meets the axis X. Transferring the light path into the initial space, the point Xo in the Λ-fractional space is transferred to the point xo of the initial space with, see
Since straight lines in the Λ-fractional space are transferred as straight lines in the initial space and the path should pass through the points a, xo, and b in the initial space, the fractional refraction problem is defined by the zigzag curve axob. It is evident that the relative slope of the line axo and the xob are not the same as in the Λ-fractional space.
Conclusion
Λ-fractional variational problems should be considered in the context of global minimization, satisfying not only the well-known Euler –Lagrange variational equation but also the additional Weierstrass-Erdmann conditions. The latter conditions yield global minimization. Applications of the proposed theory have already been presented [27], in discussing fractional mechanics, with the derivation of the governing Λ-fractional equations. Nevertheless, the remark of the globalism of the fractional variational procedures influences not only physics applications but also mathematical problems like differential equations and fractional differential geometry, (fractional geodesics).
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?




 Save to Mendeley
Save to Mendeley