Trends in Computer Science and Information Technology
Numerical analysis of forming the tri-layer non-homogeneous bellows via the hydroforming process
Pezhman Ghanbari1, Behnam Akhoundi2* and Vahid Modanloo2
2Department of Mechanical Engineering, Sirjan University of Technology, Sirjan, Kerman Province, Iran
Cite this as
Ghanbari P, Akhoundi B, Modanloo V (2023) Numerical analysis of forming the tri-layer non-homogeneous bellows via the hydroforming process. Trends Comput Sci Inf Technol 8(1): 016-022. DOI: 10.17352/tcsit.000064Copyright License
© 2023 Ghanbari P, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.Due to the complex and structural characteristics of non-homogeneous layers in hydroforming, their forming is a challenging process. In this research, the manufacturing process of three-layered bellows made of 304 stainless steel (two outer layers) and Inconel 718 (inner layer) is numerically investigated. The effects of different parameters on the forming of bellows are studied. To study the effect of friction between layers, two models are used; a model with friction between layers and a model with tied layers. It is observed that the amount of displacement in the model with a tie connection is more. The maximum values of stresses are detected in the inner region after the second stage of forming, i.e. folding. These values reduce after the spring-back step.
Introduction
Due to the promising capabilities of multi-layered metallic bellows in complex working conditions, such as high pressure, high-frequency vibration and large axial displacement, they have been used in various industries like energy, automotive and etc. Nowadays, the hydroforming process [1-22] has become an advanced and preferred technology to form the bellows because of its advantages of high efficiency and flexibility compared with different forming approaches [23-25].
The simulation of the hydroforming process of multi-layered bellow entails a number of complexities due to nonlinear material behavior, large deformation and contact. During this process, the mechanical behaviors of layers are different owing to the fact that their materials are different. Moreover, the layers are in contact and go through high levels of plastic deformation which increase the possibility of failures such as wrinkling and cracking. Furthermore, the unavoidable spring back that happens after unloading and removing the dies makes the process more complex. To keep the accuracy of hydroforming and prevent failures, it is necessary to study this process thoroughly. Many types of research were focused on the deformation behaviors of single or bi-layered bellows in hydroforming. The studies on multi-layered bellows with more than two layers are less commonly reported. To study the deformation behavior of bellows in hydroforming, some Finite Element (FE) simulations are carried out. Lee [26] simulated the single-layered bellow hydroforming process, including bulging, folding, and unloading stages using the FE method. Olabi and Alaswad [27] prepared a FE model for bi-layered tube hydroforming, and in the model, the ‘‘rigid-to-flexible surface-to-surface” contact pair was applied to describe the contact behavior between the outer layer and dies, while the ‘‘flexible-to-flexible surface-to-surface” contact pair was chosen for defining the contact behavior between the contacted layers. In research by Liu, et al. [28] on bellows with a single layer, different parameters such as initial tube thickness, crown and root diameters, convolution shape of the bellow, internal pressure, axial force and movement, die stoke, frictional coefficient, are studied. Zhu, et al. [29] investigated the effect of internal pressure on thickness change by employing the FE method. Similar studies on the effect of forming parameters are performed by Liu, et al. [30,31], Alaswad, et al. [32,33], and Faraji, et al. [34-36]. According to Liu, et al. [37], due to the complex limitations between layers in multilayer metal bellows, defects such as wrinkles and fractures can easily occur. This is a key to revealing deformation behaviors in order to get the right product. The hydroforming process of four-layer U-shaped metal bellows is modeled using finite elements and is validated by testing. The stress and strain distributions, changes in wall thickness and bellows profiles in each layer are investigated throughout the process, including the bulging, folding and spring backstages. Then the deformation behavior of bellows in different shaping conditions is discussed.
To the combined effects of tri-layered structural and non-homogeneous material characteristics of Tri-layer Non-Homogeneous Bellows (TNBs), the spring back behaviors are more complicated compared with bi-layered non-homogeneous bellows. Therefore this research investigates the effect of the bellow structure on spring back, and the bellows of different specifications and Numbers of Layers (NoLs) (NoL = 2,3) are compared. Also, the bellows of different materials are compared to study the influence of mechanical properties of the material (Inc718 and SS304) on spring back.
Forming process
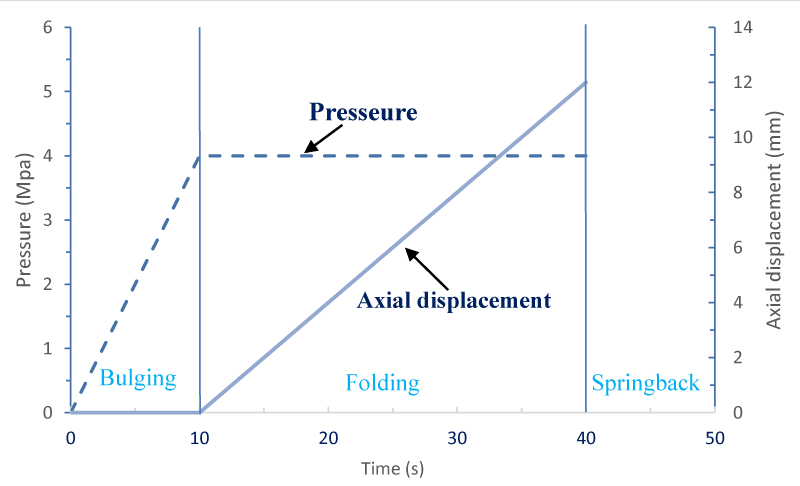
In the hydroforming method, the primary raw material is deformed into a cavity inside the die by using high-pressure fluid. This process always requires a hydraulic press, a hydroforming die, and a pressure-boosting system [38-40]. Generally, the process involves placing the primary raw piece (tube) inside the die, closing the die and applying high-pressure fluid inside the tube. The pressure of the fluid must be such that it deforms the raw material and causes the part to take the shape of the die. This process is called bulging. In the next stage (folding), without decreasing the internal pressure, an axial displacement is applied to the tube which decreases the length of the tube and forms the bellows. In the last stage, all the applied loads including internal pressure and axial displacement are removed and elastic deformation is released. The third process is known as spring back. Different stages of the process are shown in Figure 1. Moreover, Figure 2 [31] shows a schematic for pressure and axial displacement changes versus time during the forming process.
Modeling procedure
In this section, at first geometry and material properties are presented. Then, a short explanation of the FE model is given. To check the validity of the modeling, the first forming process of the two-layered bellows is modeled. The results are compared to the available results from the literature. In the next stage, forming process of the three-layered bellows is simulated. Additionally, the effect of different parameters on forming process is evaluated. To study the effect of friction on forming process, two different simulations are performed. In the first simulation, the coefficient of friction is defined between layers, and in the second simulation; surfaces are tied (bonded) together to simulate the maximum possible friction between two surfaces.
Geometry and material
The outer diameter of the initial tube is 65 mm and its length is 62 mm. After forming the length decreases to 31.4 mm. In the bi-layer geometry, the thickness of each layer is 0.12 mm and the material of the inner and outer layers are respectively Inconel 718 and Stainless steel 304 and in the tri-layer geometry, the thickness of each layer is 0.08 mm and the materials are Inconel 718 (inner layer) and Stainless steel 304 (two outer layers). Material properties that are used in the simulations are shown in Table 1 [8].
FE simulation details
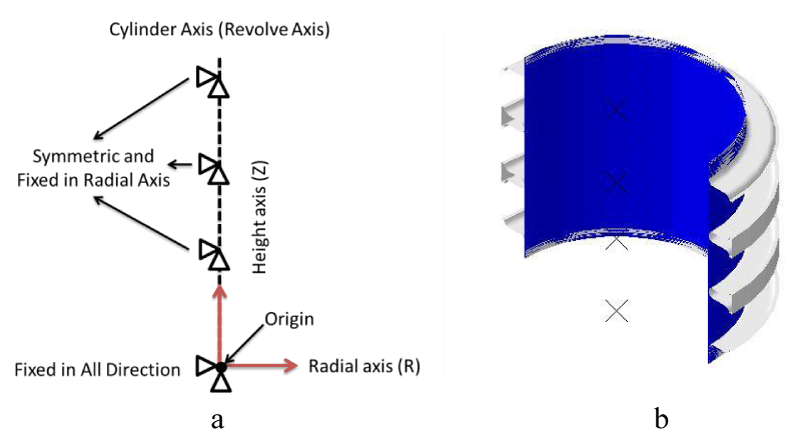
In this study, for modeling in ABAQUS software, Dynamic Explicit solver is used for steps 1 and 2, which are bulging and folding and then Static General Solver is used to create the spring back step. Also, in the load section, first, the boundary conditions of the die parts were applied as shown in Figure 3(a). In this way, in the first step, all the parts are fixed and only pressure is gradually introduced into the tube. Then, in step 2, the amount of displacement of the die parts was considered while the amount of pressure is still constant. In the spring back step, all parts of the die were removed to unload the tube. To simulate the bellows, the CAX4R element is used which is a suitable element regarding the thickness of the plates. A study on mesh convergence is carried out which shows that the optimum element size is 0.12 mm and by further increasing the elements, no considerable change in displacement and stress level is detected. At first, each layer was a separate layer, and die components were modeled in the “part”, then, in “property”, materials properties related to Inc718 and 304SS were determined. The annular die and the punch are treated as analytic rigid bodies. In the “assembly” section, all parts are located in place based on Figure 3(b).
Then, in “step” two stages of bulging and folding were defined. In the bulging step, the punch and the annular dies are fixed. By Putting on the internal pressure, the layers bulged. In the folding step, the die component moves axially towards the fixed layers end, and the internal pressure respectively flows. The layers are formed to the suitable form by the cooperation of internal pressure and axial feeding of the die component. After the completion of the second stage, a new step is made in a separate model using “create predefined field“ and in the spring backstage, the dies are removed and the internal pressure is released as shown in Figure 4.
The connection between the layers and die was defined in “interaction” The “rigid-to-flexible surface-to-surface” contact behavior is defined between the tubes and dies and the “flexible-to-flexible surface-to-surface” contact algorithm is adopted between the three layers. The value of the coefficient of friction is also given in Table 2 used by Liu, et al. [31]. The thin-walled tubes are deformable and meshed as shell element S4R (four-node doubly curved thin shell).
Bi-layered simulation and validation
To validate the desired method, first, the bi-layer model of the bellows was modeled with the mentioned specifications. Then, the values obtained at the end of the modeling were compared with the values obtained by Liu, et al. [31]. According to the obtained values, the accuracy of the work method was confirmed. The results are presented in Table 3.Results and discussion
In this study, the effect of two parameters on the hydroforming of bellows is studied. The first parameter is pressure and the second one is friction.
Study the effect of the pressure
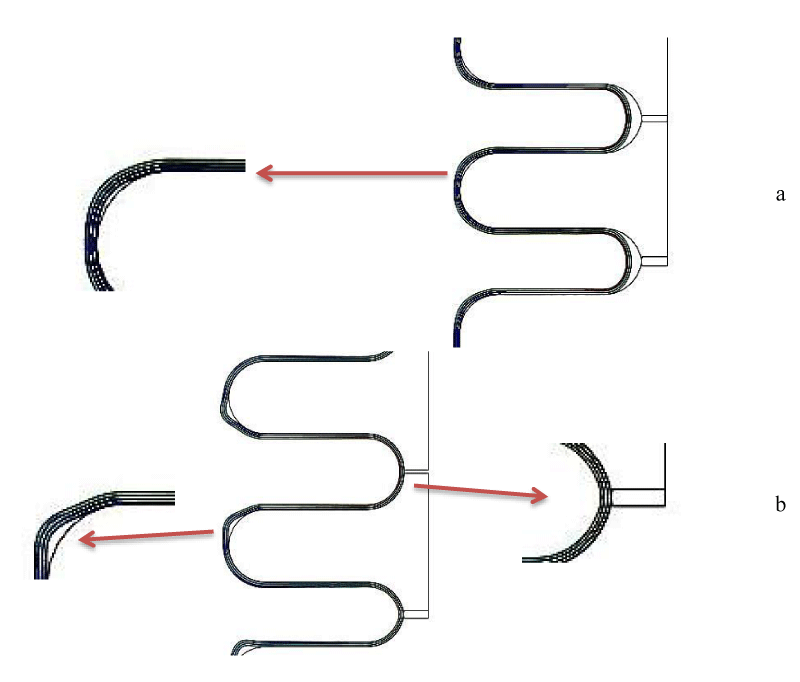
To have a complete hydroforming process without any defects, a narrow band of pressure is acceptable. To start an initial guess is applied for the value of pressure. Then based on the results, other values are tested until the correct value is found. Different values ranging from 7 MPa to 13 MPa Are tested. Finally, it is found that a pressure of 11 MPa is suitable for shaping. As shown in Figure 5(a), a pressure of less than 11MPa has prevented the complete formation of the bellows. So, the hydroforming process has not been fully implemented and has caused the parts to interfere with each other. On the other hand, excessive pressure causes the bellows to deviate from the desired shape. In such a way that the die parts do not reach each other due to excessive pressure on the inner wall and getting out of the desired size based on Figure 5(b). The reason for the improper form in the sample with the pressure below the allowable limit is probably not enough to draw off the tube by the fluid. For this reason, the heterogeneous distribution of the tube on the die surfaces is visible after forming. Also, with pressure higher than the allowable limit, the tube seems to be too stretched and wrinkled.
Study the effect of the friction
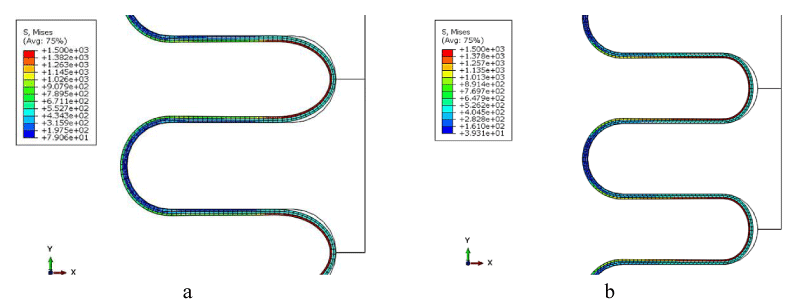
To study the effect of friction between layers, two models are created. In the first model, the coefficient of friction is defined between layers, and in the second model, this coefficient is very high in the way that two layers are tied to each other. By comparing these two models, the effect of friction between layers can be studied. As discussed in the above section, a pressure of 11 MPa is used in the hydroforming process. Simulations are performed and results are reported in the following paragraphs. Figure 6 shows the amount of von Mises stress that layers undergo as a result of the shaping process. Based on this figure, the maximum amount of stress occurs in the inner layer and its value is equal to 1500 MPa. Therefore, in the hydroforming process, the layers that are not in contact with the fluid have less stress than the inner layer. The amount of stress in both models is equal, but due to more friction in the tie, the adhesion of the layers to the die wall is more.
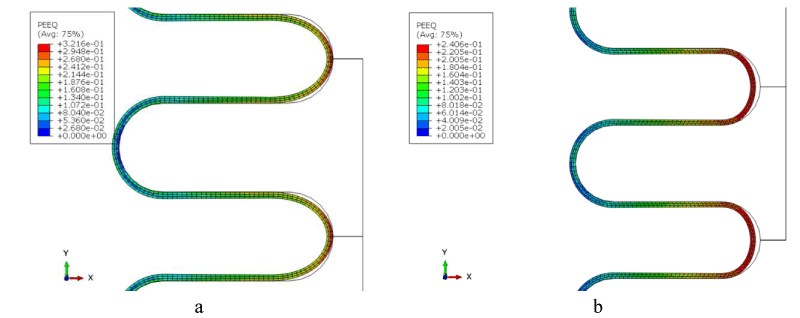
As Figure 7 presents, the maximum equivalent plastic strain in this model is equal to 0.32 for the tie model and 0.24 for the friction model. The reason for this seems to be the lack of any air gap in the tie model So that all three layers on top of each other have created an overall thickness. And this causes more strain.
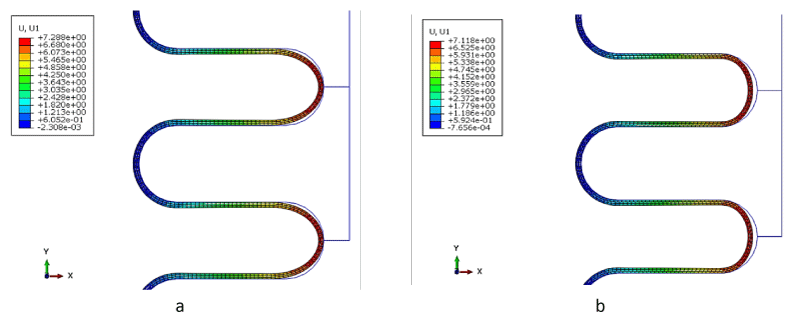
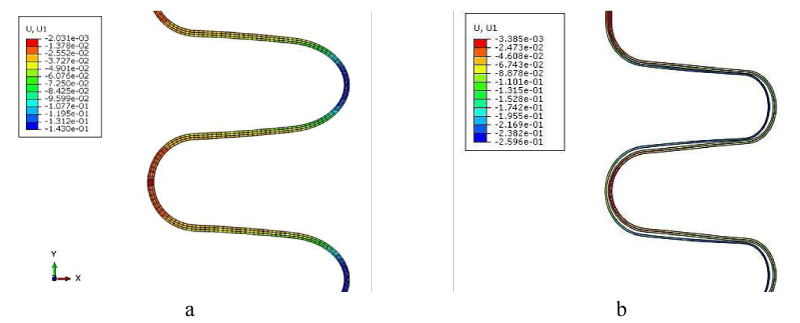
The amount of radial displacement is shown in Figure 8. As is clear, the amount of displacement in the Tie model is more than in the friction model, which is also due to the greater adhesion of the tie model. As is shown, the part of the model that is folded outwards has the most displacement and its value is a little more than 7 mm. Also, the fold has a negative inward displacement and has gone inward (in the -x direction) compared to the initial state.
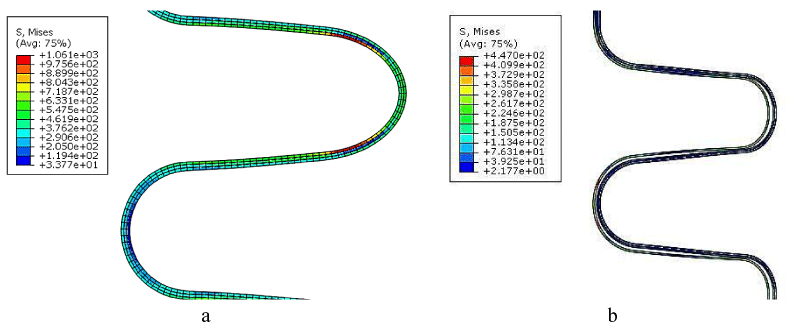
Afterward, the spring back process is investigated. Figure 9 shows the von Mises stress in the spring back. This figure reveals that the maximum amount of stress is in the inner layer and in the part where the layers have deformed and become convoluted. As it turns out, this value in the tie model is higher than this value in the friction model due to more friction between the layers. The reason for this is the adhesion between the layers in the Tai model, in which the Inc 718 layer was not allowed to discharge energy after the spring back. Also, the separation between the layers of the friction model after spring back is visible.
The amount of displacement in the spring back process is shown in Figure 10. As is depicted, the outward fold had the least and the inner fold had the most displacement. Also, it is absolutely obvious that the displacement in the friction model after the spring back process is more than the displacement in the Tie model, which is due to less friction between the layers which allows the layers without adherence to each other to continue moving in the direction of discharging existing stresses.
Table 4 represents the values for the tri-layer friction and Tie models after the folding and spring back processes.
After simulation, the residual stresses were investigated and it was observed that the residual stresses in both tri-layer models are equal after the end of the folding process as is demonstrated in Figure 11. But what is very obvious is that the amount of residual stresses after the spring back process in the friction tri-layer model is drastically reduced as is shown in Figure 12. As can be found, the inner layer which has a different material is separated from the other two layers. The reason for this is the high level of residual stress in the inner layer as well as the mechanical properties of Inc718 material, which seems to be a natural phenomenon due to the high yield stress of Inc718. It should be mentioned that the distance created between the layers in the model with friction has been observed in other studies. The amount of residual stress and main stresses after forming were listed in Tables 5,6 respectively.
A summary of the behavior of the bellows in the three stages of hydroforming
The simulation results show that the inner layer experiences the maximum stress and maximum plastic strain. The deformed radius of the inner layer is smaller than the radius of the outer layer, which means, this layer undergoes more plastic strain. Therefore, in the hydroforming process, the inner layer should have a higher forming ability. The simulation results show that after the spring back process, the residual stresses in the friction model are significantly reduced compared to the Tie model. The simulation results show that with increasing friction in the hydroforming process, the displacement of the convolution at the end of the folding process is greater. The simulation results show that the residual stresses in the tri-layer model compared to the bi-layer model with the same overall thickness are significantly reduced after the end of the spring back process. The simulation results show that after the spring back process, the height of pitch change in the tri-layer model is less than in the bi-layer model.
Conclusion
According to the finite element analysis research on tri-layer non-homogeneous bellows during the hydroforming process, the following results are confirmed:
- Initial pressure of the tri-layer model in the bulging stage of the hydroforming process with a value of 11 MPa, which shows an increase in pressure compared to the bi-layer model of 2 MPa.
- The amount of spring back in the hydroforming process of tri-layer bellows in two models of friction and Tie, which shows that more friction increases the length and height.
- Stresses related to non-homogeneous tri-layer and bi-layer bellows models show that the amount of residual stresses in the tri-layer model is significantly reduced.
- The pitch changes in this study are equal to 1.1 mm, while the pitch value of the non-homogeneous bi-layer bellows is 1.4 mm. The reason for this is the greater thickness of Inc718 material in the bi-layer model than in the tri-layer model
- The height changes in the non-homogeneous bi-layer model were 0.12 mm, while in the present study on non-homogeneous tri-layer bellows, this value has increased to 0.13mm.
- The comparison of maximum equivalent plastic strain in tri-layer non-homogeneous bellows and bi-layer non-homogeneous bellows is 0.1075, which indicates that the formation in this study has improved due to layer increase.
- Cui X-L, Teng B, Yuan S. Hydroforming process of complex T-shaped tubular parts of nickel-based superalloy. CIRP Journal of Manufacturing Science and Technology. 2021; 32:476-490.
- Ma J, Yang L, Liu J, Chen Z, He Y. Evaluating the quality of assembled camshafts under pulsating hydroforming. Journal of Manufacturing Processes. 2021; 61:69-82.
- Marlapalle BG, Hingole RS. Predictions of formability parameters in tube hydroforming process. SN Applied Sciences. 2021; 3 (6):606
- Hwang Y-M, Manabe K-I. Latest hydroforming technology of metallic tubes and sheets. 2021; 11.
- Ma Y, Chen S-f, Chen D-y, Banabic D, Song H-w, Xu Y, Zhang S-h, Fan X-s, Wang Q. Determination of the forming limit of impact hydroforming by frictionless full zone hydraulic forming test. International Journal of Material Forming. 2021; 14:1221-1232.
- Pourhamid R, Shirazi A. A comprehensive damage criterion in tube hydroforming. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture. 2021; 235 (3):417-430.
- Eftekhari Shahri SE, Lakhi M, Taheridoustabad I. Numerical and experimental investigation of the ultrasonic vibration effects on the tube hydroforming process in a die with a square cross-section. The International Journal of Advanced Manufacturing Technology. 2023; 1-11.
- Zhang J, Dai M, Wang F, Tang W, Zhao X. Buckling performance of egg-shaped shells fabricated through free hydroforming. International Journal of Pressure Vessels and Piping. 2021; 193:104435.
- Zhang J, Dai M, Wang F, Tang W, Zhao X, Zhu Y. Theoretical and experimental study of the free hydroforming of egg-shaped shell. Ships and Offshore Structures. 2022; 17(2):257-267.
- Liu S, Wang H, Lan W, Liu Y, Che J, Ma S. Repairing Damaged Screen Pipes with Tube Hydroforming: Experiments and Feasibility Analysis. Machines. 2022; 10 (5):391.
- Liu W, Chen Y-Z, Hu L, Zhang Z-C. Deformation of large curved shells using double-sided pressure sheet hydroforming process. International Journal of Lightweight Materials and Manufacture. 2022; 5 (3):397-410.
- Piccinini A, Cusanno A, Palumbo G, Zaheer O, Ingarao G, Fratini L. Reshaping End-of-Life components by sheet hydroforming: An experimental and numerical analysis. Journal of Materials Processing Technology. 2022; 306:117650.
- Yuan S. Modern hydroforming technology. Springer Nature. 2022.
- Zhang J, Liu X, Zhan M, Wang F, Zhao X. Hydroforming and buckling of toroids with polyhedral sections. Ships and Offshore Structures. 2022; 1-11.
- Zhang J, Wang R, Zeng Y. Hydroforming rules and quality control parameters analysis for the metal bipolar plate. Engineering Failure Analysis. 2022; 132:105919.
- Cusanno A, Ingarao G, Palumbo G, Fratini L, Piccininni A. Optimization of the sheet hydroforming process parameters to improve the quality of reshaped EoL components. Materials Research Proceedings 25.
- Piccininni A, Cusanno A, Ingarao G, Palumbo G, Fratini L. Optimization of the sheet hydroforming process parameters to improve the quality of reshaped EoL components.
- Zhang J, Cheng P, Wang F, Tang W, Zhao X. Hydroforming and buckling of an egg-shaped shell based on a petal-shaped preform. Ocean Engineering. 2022; 250:111057.
- Huang Y, Li J, Yang J, Peng Y, Zhang W. Simulation Analysis of Torsion Beam Hydroforming Based on the Fluid-Solid Coupling Method. Chinese Journal of Mechanical Engineering. 2023; 36 (1):3.
- Mohseni A, Rezapour J, Gohari Rad S, Rajabiehfard R. Numerical and experimental investigation of dynamic tube hydroforming to examine the prediction on it by genetic programming. International Journal of Structural Integrity. 2023.
- Xia L-L, Zhang S-H, Xu Y, Chen S-F, Khina BB, Pokrovsky AI. Deformation characteristics and inertial effect of complex aluminum alloy sheet part under impact hydroforming: experiments and numerical analysis. Advances in Manufacturing. 2023; 1-18.
- Bell C, Corney J, Zuelli N, Savings D. A state-of-the-art review of hydroforming technology: Its applications, research areas, history, and future in manufacturing. International Journal of Material Forming. 2020; 13:789-828.
- Alaswad A, Benyounis K, Olabi AG. Tube hydroforming process: A reference guide. Materials & Design. 2012; 33:328-339.
- Sedighi M, Shamsi M. A new approach in producing metal bellows by local arc heating: a parametric study. The International Journal of Advanced Manufacturing Technology. 2017; 93:3211-3219.
- Si DH, Liu YG, Ma W. Research the influence of curved shape on the multilayer bellows. In: Applied Mechanics and Materials. Trans Tech Publ. 2013; 2740-2743.
- Lee S. Study on the forming parameters of the metal bellows. Journal of Materials Processing Technology. 2002; 130:47-53.
- Olabi A, Alaswad A. Experimental and finite element investigation of formability and failures in bi-layered tube hydroforming. Advances in Engineering Software. 2011; 42(10):815-820.
- Liu J, Liu Y, Li LY, Li X, Yang SF, Geng YH, Liu FY. Springback analysis of thin-walled stainless steel bellow in hydroforming. In: Advanced Materials Research. Trans Tech Publ. 2015; 855-858.
- Zhu Y, Wan M, Zhou Y, Liu Q, Li Y, Zheng N, Pi K. Hydroforming of complicated thin-walled circular parts with irregular sections by using moving dies. Acta Aeronautica et Astronautica Sinica. 2012; 33(5):912-919.
- Liu J, Li H, Liu Y, Li L, Sun C. Size effect related hydroforming characteristics of thin-walled 316-L bellow considering pressure change. The International Journal of Advanced Manufacturing Technology. 2018; 98:505-522.
- Liu J, Liu Y, Li L, Li X. Springback behaviors of bi-layered non-homogeneous bellows in hydroforming. The International Journal of Advanced Manufacturing Technology. 2017; 93:1605-1616.
- Alaswad A, Benyounis K, Olabi A. Finite element comparison of single and bi-layered tube hydroforming processes. Simulation Modelling Practice and Theory. 2011; 19(7):1584-1593.
- Alaswad A, Olabi A, Benyounis K. Integration of finite element analysis and design of experiments to analyze the geometrical factors in bi-layered tube hydroforming. Materials & Design. 2011; 32 (2):838-850.
- Faraji G, Besharati M, Mosavi M, Kashanizadeh H. Experimental and finite element analysis of parameters in manufacturing of metal bellows. International Journal of advanced manufacturing technology. 2008; 38.
- Faraji G, Hashemi R, Mashhadi MM, Dizaji A, Norouzifard V. Hydroforming limits in metal bellows forming process. Materials and Manufacturing Processes. 2010; 25(12):1413-1417.
- Faraji G, Mashhadi MM, Norouzifard V. Evaluation of effective parameters in metal bellows forming process. Journal of Materials Processing Technology. 2009; 209 (7):3431-3437.
- Jing L, Zhiyong L, Yang L, Lanyun L. Deformation behaviors of four-layered U-shaped metallic bellows in hydroforming. Chinese Journal of Aeronautics. 2020; 33 (12):3479-3494.
- Modanloo V, Alimirzaloo V. Minimization of the sheet thinning in hydraulic deep drawing process using response surface methodology and finite element method. International Journal of Engineering. 2016; 29(2):264-273.
- Modanloo V, Gorji A, Bakhshi-Jooybari M. Effects of forming media on hydrodynamic deep drawing. Journal of Mechanical Science and Technology. 2016; 30:2237-2242.
- Modanloo V, Gorji A, Bakhshi-Jooybari M. A comprehensive thinning analysis for hydrodynamic deep drawing assisted by radial pressure. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering. 2019; 43:487-494 .
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

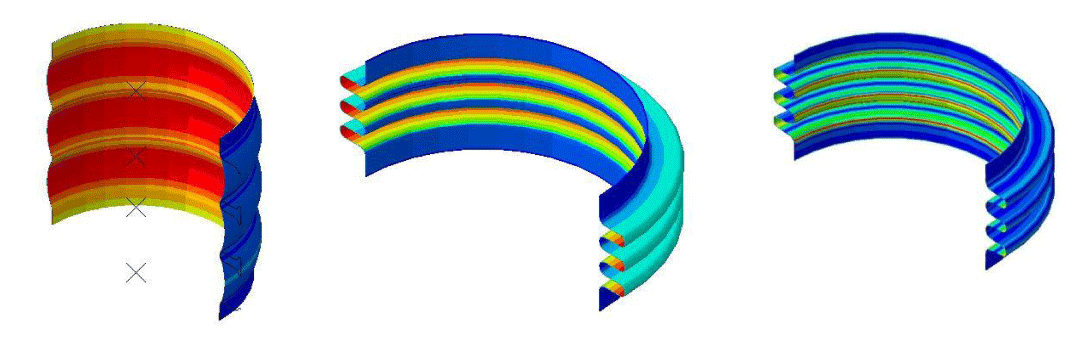
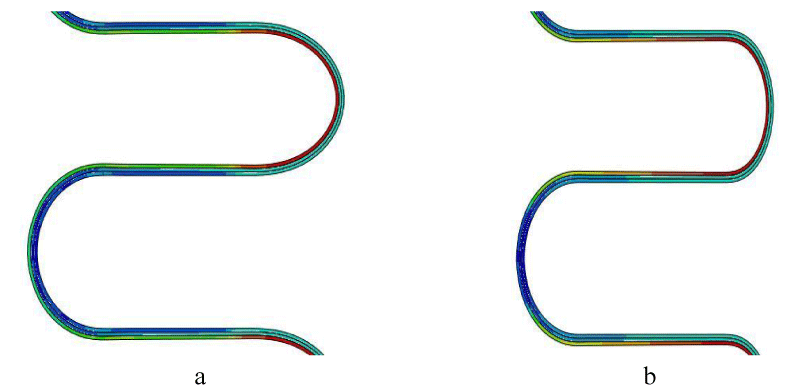
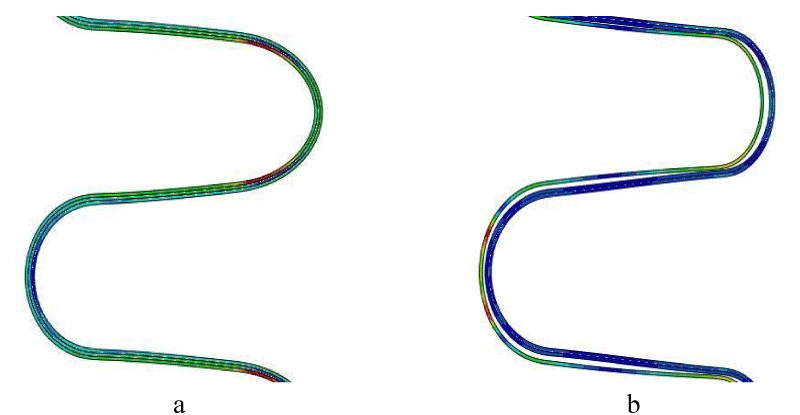


 Save to Mendeley
Save to Mendeley
