Trends in Computer Science and Information Technology
OG-SLAM: A real-time and high-accurate monocular visual SLAM framework
Boyu Kuang*, Yuheng Chen and Zeeshan A Rana
Cite this as
Kuang B, Chen Y, Rana ZA (2022) OG-SLAM: A real-time and high-accurate monocular visual SLAM framework. Trends Comput Sci Inf Technol 7(2): 047-054. DOI: 10.17352/tcsit.000050Copyright License
© 2022 Kuang B. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.The challenge of improving the accuracy of monocular Simultaneous Localization and Mapping (SLAM) is considered, which widely appears in computer vision, autonomous robotics, and remote sensing. A new framework (ORB-GMS-SLAM (or OG-SLAM)) is proposed, which introduces the region-based motion smoothness into a typical Visual SLAM (V-SLAM) system. The region-based motion smoothness is implemented by integrating the Oriented Fast and Rotated Brief (ORB) features and the Grid-based Motion Statistics (GMS) algorithm into the feature matching process. The OG-SLAM significantly reduces the absolute trajectory error (ATE) on the key-frame trajectory estimation without compromising the real-time performance. This study compares the proposed OG-SLAM to an advanced V-SLAM system (ORB-SLAM2). The results indicate the highest accuracy improvement of almost 75% on a typical RGB-D SLAM benchmark. Compared with other ORB-SLAM2 settings (1800 key points), the OG-SLAM improves the accuracy by around 20% without losing performance in real-time. The OG-SLAM framework has a significant advantage over the ORB-SLAM2 system in that it is more robust for rotation, loop-free, and long ground-truth length scenarios. Furthermore, as far as the authors are aware, this framework is the first attempt to integrate the GMS algorithm into the V-SLAM.
Introduction
Simultaneous Localization and Mapping (SLAM) widely appear in computer vision, autonomous robotics, and remote sensing [1-3]. The SLAM system can be generally summarized as Laser SLAM (L-SLAM) and Visual SLAM (V-SLAM) [4]. Ref. [5] claims that the L-SLAM has higher accuracy but is more cumbersome and expensive. The V-SLAM has a lower cost and is more flexible. Moreover, the V-SLAM is more similar to the human vision system, which has wider research and application prospects [5]. For example, Refs. [6-8] apply the V-SLAM into 3D environmental sensing, Refs. [9-11] work on the rover autonomy, and Refs. [12-14] addresses drone navigation. However, the process of V-SLAM is complicated and challenging. The V-SLAM applies the camera system as the input sensor, which attempts to recover the three-dimensional (3D) structure using two-dimensional (2D) images from the pinhole camera model [15]. The dimension reduction (3D to 2D) loses numerous information, while the V-SLAM system aims to approach the original 3D information through the multiple view geometry (MVG).
The V-SALM can be understood as a special case of the MVG. The basic task of MVG is to estimate the relative motion between inter-frames, which corresponds to the localization part of V-SLAM. Then, the V-SLAM system connects with a mapping part to project the 2D pixels to the 3D coordinates. The V-SLAM is a real-time and dynamic process, which can be understood as an MVG corresponding with timestamps [3]. Localization is the main focus of this study, which can achieve the relative pose estimation between inter-frames, and the pose consists of position and orientation.
This study proposes a modified V-SLAM framework (OG-SLAM), integrated with Oriented FAST and Rotated Brief (ORB) [16] feature and Grid-based Motion Statistics (GMS) algorithm. This study mainly contributes to these three aspects:
By integrating the motion smoothness into the V-SLAM system, the OG-SLAM framework has significantly improved the accuracy without reducing the real-time performance.
The OG-SLAM framework improves the robustness of the rotation, loop-free, and long ground-truth length of the V-SLAM system.
As the authors are aware, this study is the first trial by integrating the ORB and GMS algorithms into the monocular V-SLAM system.
The study is organized as follows: Section 3 introduces the method and mathematical basis of the OG-SLAM framework. Section 4 discusses the dataset used in this study and the corresponding results. Finally, the conclusion is drawn in the end.
Related works
The inter-frame estimation in V-SLAM corresponds to the estimation of epi-polar geometry in MVG [17]. The overall V-SLAM refers to an incremental result from iterations of multiple epi-polar geometries. Thus, the estimation error in one inter-frame estimation iterates and accumulates to the following inter-frame estimation, which is called drift-error (or drift). Drift is one of the main challenges for current V-SLAM in large scene reconstruction tasks [5]. There are two approaches for decreasing the drift, which is local optimization and global optimization.
The conventional solutions are global optimization, which corresponds to the optimization and loop-closing steps in the monocular SLAM system. Global optimization can be classified as linear optimization (such as Kalman filter [18]), nonlinear optimization (such as extended Kalman filter [19]) and bundle adjustment (BA) [20]. However, the best performance comes from BA, which significantly accelerates V-SLAM development [21]. Although BA significantly decreases the drift error, the result still requires further improvements [5,22]. Loop-closure improves the V-SLAM performance by closing the camera trajectory and the reconstructed map, which significantly improves the accuracy of the V-SLAM system [16]. However, in many cases, it is challenging to accomplish a closed-loop, for example, large-scale navigation and target tracking, which leads to high demand for the loop-free V-SLAM.
Another solution is to reduce the drift individually, named local optimization in this study. The local optimization focuses on each inter-frame camera pose estimation, a process of inter-frame information association. Some attempts use local optimization, for example, SIFT-SLAM [23] and NeroSLAM [6]. In computer vision, one method of inter-frame information association is feature matching. This study uses the GMS algorithm [24] based on motion smoothness to screen out the incorrect matches. Although the GMS algorithm has improved many studies [25-27], the visibility of GMS in V-SLAM has not been systematically discussed.
Ref. [5] claims that even if many efforts have been made (such as Ref. [28], Ref. [29], and Ref. [30], the drift is still a significant challenge for the monocular V-SLAM system.
Method
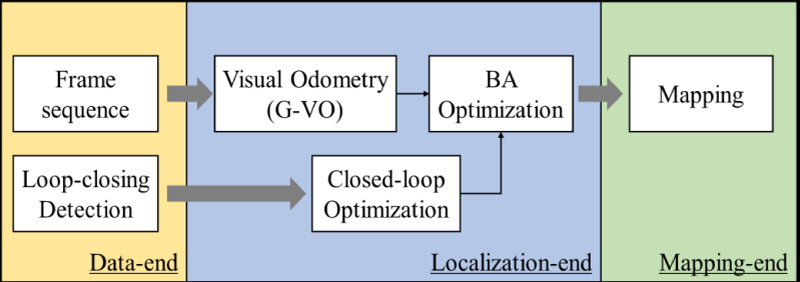
The general structure of the proposed ORB-GMS-SLAM (OG-SLAM) framework is shown in Figure 1, where the overall process can be divided into three parts. The Data-end reads and prepares data, the Localization-end estimates the key-frame trajectory, and the Mapping-end conducts the mapping tasks.
Data-end
Data-end is a data input and preparation module. It is noteworthy that the closed loop is a correction mechanism that is only triggered when the camera returns to the same historical position. Thus, excessive dependence on closed-loop can significantly limit the V-SLAM application. Therefore, the OG-SLAM system divides the input data into input frame data and closed-loop detection data and introduces two parallel data streams into the Localization-end. This framework design increases versatility and reduces closed-loop dependence.
Localization-end
The input frame data is then frame-by-frame passed to the Localization-end along the time stamps. Localization-end consists of three modules, GMS-based visual odometer (G-VO), BA optimization, and closed-loop optimization. The G-VO estimates the relative motion (rotation and translation) between consecutive frame-pairs, which strongly impacts the result of the inter-frame information association. This problem corresponds to feature matching and epi-polar geometric constraints in the feature-based V-SLAM system. According to Ref. [29], GMS is a robust feature matching algorithm, which significantly increases the robustness of feature matching without making the computation expensive [29]. Therefore, OG-SLAM uses the Fast Library for Approximate Nearest Neighbors (FLANN) algorithm [31] to generate matches, which are then filtered out false matches using GMS.
More specifically, the G-VO firstly constructs an image pyramid, which is constructed with eight layers, and the scaling factor is 1.2. Then, the G-VO extracts the potential ORB key points [32] using the Feature from Accelerated Segments Test (FAST) [33] algorithm on each layer. Ref. [29] recommend extracting 1000 ORB key points per frame when the resolutions are between 512×384 pixels and 752×480 pixels [29]. Considering the G-VO decreases the ORB key-point amount (OKA) by filtering out the false GMS matches, the OG-SLAM can handle more features to involve more associated information. G-VO sets the OKA per frame by 1800. The details of choosing OKA are discussed in Section 4. For better use of the spatial information covered by the entire frame, G-VO uses the grid to divide the image into many sub-regions and extracts the equal OKA from each sub-region.
As shown in Figure 2, the p is the target pixel. The luminance of this pixel is LuminancePixel (LP), then only compares the luminance of LP with the four yellow pixels (1, 5, 9, and 13). The luminance (LPN) of NeighborPixel (PN) and a threshold ThresholdValue (TV) is set to improve the difference between p and pN. This pixel is considered to be a potential feature point when the LP values of p and LPN value of PN satisfy Equation (1) [32], where KPpotential represents the potential key point.
The Harris response values [34] of the potential ORB key points are then calculated, and the first 1800 key points are taken as the ORB key points. Then, the ORB descriptor is generated with the orientation calculated using the Intensity Centroid algorithm [32].
According to Ref. [29], the technology of extracting many key points has been implemented, but eliminating invalid matches is the current main challenge. Feature matching is actually a task of neighborhood similarity evaluation. GMS claims that the motion smoothness supports more matches in the neighborhood [29], which transfers the feature matching process to a statistic of the motion smoothness. The matches which are satisfied with the GM’s criterion are named GMS-matches in this study.
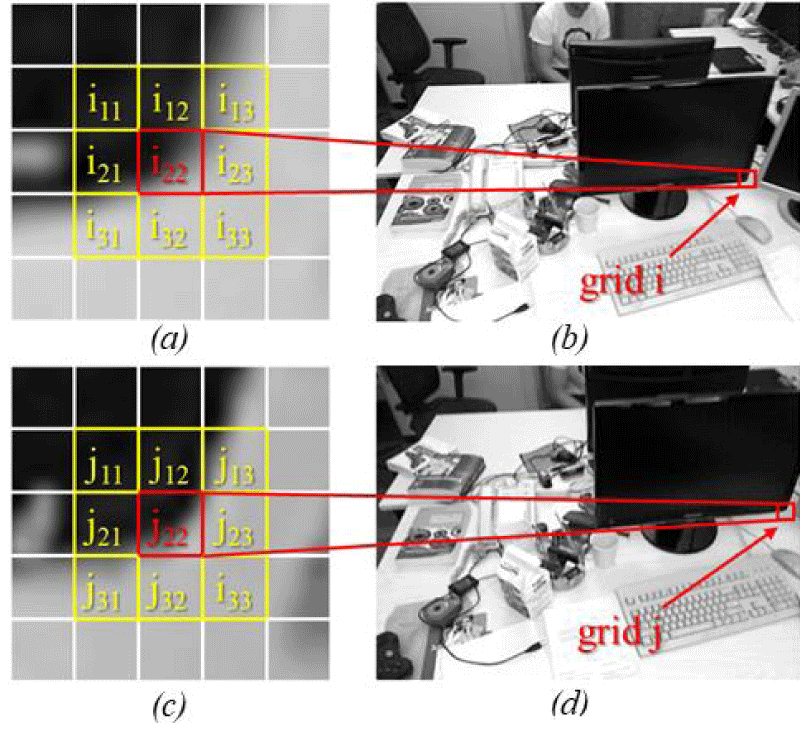
The only relevant area of the GMS is the neighborhood. G-VO utilizes grids to segment the frame first, then conducts the GMS on the neighbor grids. As shown in Figure 3, this process is named grid-GMS. The frame is segmented into many 20×20pixels in small cells. The size of the experimental images in this study is 640×480 pixels, so the entire image is divided into 32×24 (= 768) grids without overlapping. Thus, when the potential ORB feature points are 1800, the average key points (nave) is 2.34375 key points per grid. The G-VO also sets an amplification factor, α = 6, to ensure enough margin for counting supported GMS matches (GMS-supporters).
As shown in Figure 3, the grids i and j contain the target ORB match, mij. represents the GMS-supporters amount within the nine neighboring grids (the yellow grids), thus the match-score (sgridij) is calculated according to Equation (2). The criterion for the matching is Equation (3). In this study, the value of τ is 9.186. Thus, when the GMS-supporter amount is more significant than eight, the matching is considered the GMS-match.
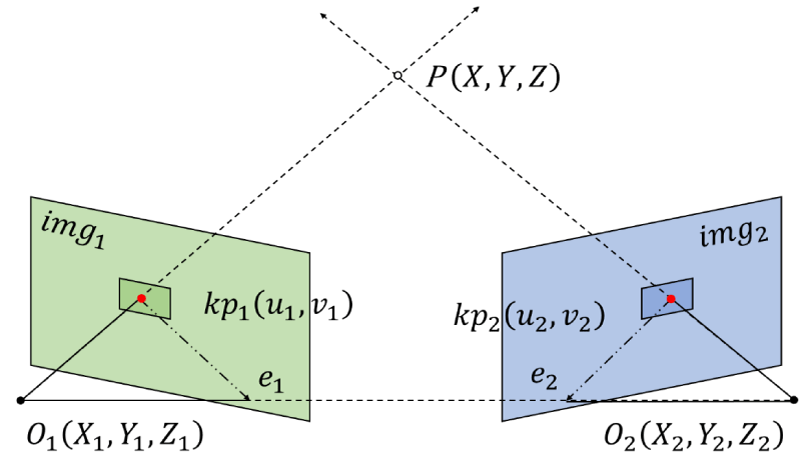
The impact of the GMS algorithm on inter-frame and key-frame pose estimation has been discussed below. The only difference between inter-frame estimation and key-frame estimation is the implication of img1 and img2 in Figure 4, which has nothing related to the mathematical process.
In Euclidean space, the image plane and camera can be represented by a vector. Therefore, the direction represents the camera orientation, and the starting point represents the camera location. According to Ref. [35], the motion between two 3D vectors can be represented by one rotation and translation [35]. Figure 4 shows an epi-polar constraint between images img1 and img2. p is a real point corresponding to the key points Kp1 and Kp2. X, Y, and Z are its 3D coordinates. K is the essential matrix, while R and t represent the rotation and translation. Equation (4) is the relationship between the pixel and the real point [3].
According to Ref. [15], the transformation between Kp1 and Kp2 can be deduced through Equation (5), (6), (7), (8), (9) [15], where Kp1 and Kp2 is the homogeneous coordinate of Kp1 and Kp2, and u and v respectively represent its 2D coordinates. The first digit in subscript corresponds to the index of the image, and the second digit corresponds to the different matches [15].
The , and F in Equation (5) is expanded to Equation (6):
Then, Equation (6) can be rephrased to the form of Equation (7):
Equation (7) can be decomposed to the form of Equation (8) to further achieve vector f:
Equation (9) is the expanded form of Equation (8):
It is obvious that a match as shown in Figure 4 can only provide one constraint. Therefore, Ref. [15] further introduces Equation (10) [15] as an additional constraint to calculate the F[15].
Equation (11) converts F into a vector, f and Equation (12) proposes f as the homogeneous form of f, which can achieve scale invariance.
The unknown amount in f is 9. Equation (13) shows the unknown amount in f is 8 (nmt), and it is noteworthy that a certain f is correlated with a certain motion (R and t).
Assuming there is a nine-dimensional (9D) coordinate system, which contains the f. Considering the scale invariance, f is a “straight line” that goes through the origin. Therefore, the projection from a “straight line” f to any f33-adjacent 2D coordinate plane is also a straight line that goes through the origin. Their respective slopes are the corresponding values in , which can be found in Equation (12). However, the f estimated through different matches-pair is a group of splattering. This translates the motion estimation into solving the overdetermined Equations or linear regression in a high-dimensional coordinate system. This study follows the same solution as the ORB-SLAM2 system.
It is noteworthy that, when the tracking key-points are less than 50 (nkft), the G-VO key-frame detection is triggered, thus the amount of matches available in any motion estimation is equal to or greater than 50. The condition with 50 key points is named extreme condition, the performance of which can represent its robustness to the scenario of large rotation, high illumination variation, heavy vibration, loop-free, and long ground-truth trajectory length (GTL). Equation (14) uses the fSet to contain all the f estimations, the Nf is calculated using Equation (15).
During the extreme condition, the ORB-SLAM2 system directly conducts the least-squares method to the fSet ; however, the matches used in OG-SLAM are the GMS matches. This study uses Equation (16) to define a score, Scoremval, which quantifies the value of matches for motion estimation in the 9D coordinate system. The akd corresponds to the average key-frame drift.
Because of the assumption of motion smoothness, the GMS-matches should contain higher Scoremval, therefore OG-SLAM should provide more accurate motion estimation. All the above mathematic deductions are proved by experimental results in Section 4.
Mapping-end
The OG-SLAM is a monocular SLAM system. The theoretical support is triangulation. Depending on the specific V-SLAM application, various mapping approaches can be implemented as the Mapping-end. For example, block-matching can be used for dense 3D reconstruction [36], or sparse grid maps can be constructed from points and lines [37]. Considering that Mapping is not the focus of this study, thus the Mapping-end does not explore in very detail in this study.
Experiments and analysis
The experimental hardware is the ThinkStation PC workstation with Inter(R) Core(TM) i7-7700 CPU, 32 GB memory, and NVIDIA GTX1080 GPU. The platform is Ubuntu 18.04 system.
Datasets and Absolute Trajectory Error
In this study, the four datasets from the RGB-D SLAM database [38] are selected for experiments. Table 1 shows the specific information of the four datasets. Where idx is the index of each dataset. D represents the dataset duration in-unit second (s). GTL represents the ground-truth trajectory length in unit meter (m). ATV represents the average translational velocity in unit meters per second (m/s). AAV represents the average angular velocity in unit degree per second (deg/s). SName represents the sequence name of the dataset in the RGB-D SLAM database.
The main motion in dataset 1 is translation along the X, Y, Z axis with a speed of 0.244 m/s, which has the fastest ATV except dataset 4. In addition, dataset 1 contains only a small AAV with a duration of 30.09 s and a total motion distance of 7.112 m. This is a fundamental and straightforward dataset. Thus, this study uses this dataset as a baseline experiment. Dataset 2 is similar to dataset 1, which is still primarily a translation, and dataset 2 significantly reduces the AAV to evaluate the rotation robustness. Dataset 3 moves the experimental scene to an empty lobby where the camera moves around the desk and returns to its original position, which triggers the close-loop. Dataset 4 is the most complex dataset with large ATV and AAV. Moreover, Dataset 4 has no closed loop, which is used to compare with dataset 3 to verify the interaction between GMS and closed-loop.
Considering the monocular V-SLAM system initialization is unstable, the results provided in this study are the average value of ten repeated experiments, and the extreme results with high-bias key-frame amount have been deleted.
The ORB key-point amount per frame
According to Ref. [39], real-time is very important for the V-SLAM system [39]. In feature engineering, the more key points can remain, the more information can significantly decrease the frame-per-second (fps). The comparison system used in this study is the ORB-SLAM2 system [29], which uses the default 1000 OKA. The OG-SLAM framework filters out the false GMS matches. Therefore, it is evident that the OG-SLAM requires more than 1000 OKA. Fossum states that the frame rate of a typical camera is at least 30 fps because the human eye can feel inconsistency when the frame rate is less than 30 fps [40]. Therefore, to balance the OKA and the real-time performance, the OG-SLAM system uses 30 fps as a real-time watershed, and all the OG-SLAM have to be 30 fps or more.
The experimental results show that the optimal ORB feature extraction amount is 1,800, and the specific experimental records are shown in Table 2. The idx stands for different dataset numbers. ORB-SLAM2 suggests the high-resolution image (such as the image in the KITTI database, 1242×370 pixels) should use 2000 OKA, thus OG-SLAM starts from 2000 OKA, and then half-converges to the eventual OKA. As the red block shown in Table 2, the fps of OG-SLAM crosses the 30 fps between 1800 and 1850 in dataset 3. Therefore, the OKA of OG-SLAM is set to 1800 to keep the real-time performance.
Result and discussion
This study uses the ORB-SLAM2 system as a comparison to evaluate the accuracy and real-time performance of the OG-SLAM framework. According to Mur-Artal, the ORB-SLAM2 system is the advanced version of the ORB-SLAM system, and ORB-SLAM2 achieves the best result among all other state-of-art V-SLAM systems [29,39].
The ORB-SLAM2 has been used in two settings, and both of them are compared with the OG-SLAM framework. The O1000 represents the default ORB-SLAM2 model, which extracts 1000 OKA. The O1800 represents another ORB-SLAM2 model with 1800 OKA. G1800 represents the OG-SLAM framework with 1800 OKA.
KFA represents the key-frame amount. ATER represents the root-mean-square error of absolute trajectory error (ATE). The ATER is calculated using the online RGB-D SLAM benchmark, which compares the key-frame trajectory with the ground truth data [38]. fps stands for the frame per second. accIpv corresponds to the accuracy improvement, fpsDcs corresponds to the fps decrease. The left column is the comparison result between O1000 and G1800, and the right column is the comparison result between O1800 and G1800. DER represents the drift error ratio, which is obtained by Equation (17).
As shown in Table 3, dataset 1 achieves the best accIpv compared with O1000, 74.56%. However, the ATER value of O1800 is 0.017, while G1800 is 0.014. Both of them have decreased significantly compared to 0.053 for O1000. This shows that increasing the number of initial feature points can greatly improve the V-SLAM system accuracy. However, dataset 1 is difficult to distinguish the performance of the local optimization, G-VO, in the OG-SLAM framework.
As shown in Table 4, dataset 2 can be found that the accuracy of the ORB-SLAM2 system is greatly improved, when the AAV is significantly decreased. The OG-SLAM accIpv for datasets 1 and 2 are basically the same, but the ORB-SLAM2 accIpv has numerous differences. This illustrates that the OG-SLAM has better robustness for rotation compared to ORB-SLAM2 systems.
As shown in Table 5, dataset 3 has the longest GTL. The drift error is a cumulative value, thus dataset 3 contains the highest DER compared to the other three datasets. However, compared to the ORB-SLAM2, the OG-SLAM still achieves 22.21% and 13.42% accIpv corresponding to O1000 and O1800.
Dataset 4 has no closed-loop. As mentioned in Section 3, this study uses dataset 4 to evaluate the robustness of OG-SLAM under loop-free conditions. As shown in Table 6, simply increasing OKA does not play a positive role in the ORB-SLAM2 system, However, OG-SLAM still achieves more than 15% accIpv. Therefore, the OG-SLAM has better robustness in loop-free conditions.
Then, compare the fpsDcs value among the four datasets. When the OKA of ORB-SLAM2 is 1000, the OG-SLAM significantly improves the accuracy, and it is also noteworthy that all the fps is higher than 30 fps. When the OKA of ORB-SLAM2 is 1800, the OG-SLAM still improves around 18.41% accuracy while the fps is basically the same as the O1800 model of ORB-SLAM2. This means the main reason for the fpsDcs is the OKA increase, but the proposed G-VO does not calculate of V-SLAM becomes more expensive.
Conclusion
This study proposes a real-time high-accuracy monocular V-SLAM framework using ORB feature extraction and a GMS feature matching algorithm. The four datasets are used to test the translation, rotation, GTL, and closed-loop robustness of the OG-SLAM framework. Compared with the ORB-SLAM2 system, the OG-SLAM framework achieved a maximum accuracy improvement of 74.56% in dataset 1. Furthermore, in the case of the same OKA, the OG-SLAM framework still achieves an average accuracy improvement of 18.41% without reducing the real-time performance. The OG-SLAM framework proposed in this study is effective in the monocular V-SLAM. Under the premise of ensuring real-time performance, the accuracy of key-frame trajectory estimation has significantly improved. OG-SLAM has superior performance compared to ORB-SLAM2.
- Saputra MRU, Markham A, Trigoni N. Visual SLAM and Structure from Motion in Dynamic Environments. ACM Comput Surv. 2018; 51:1–36.
- Geromichalos D, Azkarate M, Tsardoulias E, Gerdes L, Petrou L, Perez Del Pulgar C. SLAM for autonomous planetary rovers with global localization. J F Robot. 2020; 37: 830–847.
- Li G, Geng Y, Zhang W. Autonomous planetary rover navigation via active SLAM. Aircr Eng Aerosp Technol. 91: 60–68.
- Francis SLX, Anavatti SG, Garratt M, Shim H. A ToF-Camera as a 3D Vision Sensor for Autonomous Mobile Robotics. Int J Adv Robot Syst. 12: 156.
- Younes G, Asmar D, Shammas E, Zelek J. Keyframe-based monocular SLAM: design, survey, and future directions. Rob Auton Syst. 98: 67-88.
- Yu F, Shang J, Hu Y, Milford M. NeuroSLAM: a brain-inspired SLAM system for 3D environments. Biol Cybern. 113: 5-6. 515-545,
- Nüchter A, Lingemann K, Hertzberg J, Surmann H. 6D SLAM - 3D mapping outdoor environments. J F Robot. 2007; 24: 699-722.
- Kuang B, Rana Z, Zhao Y. A Novel Aircraft Wing Inspection Framework based on Multiple View Geometry and Convolutional Neural Network. Aerosp Eur Conf 2020.
- Hewitt RA. The Katwijk beach planetary rover dataset. Int J Rob Res. 37: 3-12, 2018.
- Furgale P, Carle P, Enright J, Barfoot TD. The Devon Island rover navigation dataset. Int J Rob Res. 2012; 31: 707–713.
- Kuang B, Rana ZA, Zhao Y. Sky and Ground Segmentation in the Navigation Visions of the Planetary Rovers. Sensors (Basel). 2021 Oct 21;21(21):6996. doi: 10.3390/s21216996. PMID: 34770302; PMCID: PMC8588092.
- Compagnin A. Autoport project: A docking station for planetary exploration drones. AIAA SciTech Forum - 55th AIAA Aerosp Sci Meet. 2017.
- Dubois R, Eudes A, Fremont V. AirMuseum: a heterogeneous multi-robot dataset for stereo-visual and inertial Simultaneous Localization and Mapping. IEEE Int Conf Multisens Fusion Integr Intell Syst 2020; 2020: 166-172.
- Chiodini S, Torresin L, Pertile M, Debei S. Evaluation of 3D CNN Semantic Mapping for Rover Navigation. 2020 IEEE 7th International Workshop on Metrology for AeroSpace (MetroAeroSpace). 2020; 32–36.
- Opower H. Multiple view geometry in computer vision. Opt. Lasers Eng. 37;1: 2002; 85–86.
- Williams B, Cummins M, Neira J, Newman P, Reid I,Tardós J. A comparison of loop closing techniques in monocular SLAM. Rob Auton Syst 57; 12: 2009; 1188–1197.
- Polvi J, Taketomi T, Yamamoto G, Dey A, Sandor C, Kato H. SlidAR: A 3D positioning method for SLAM-based handheld augmented reality Comput Graph 2016; 55: 33-43.
- Chen SY. Kalman Filter for Robot Vision: A Survey. IEEE Trans Ind Electron 59: 4409-4420.
- Castellanos JA, Neira J, Tardós JD. Limits to the consistency of EKF-based SLAM. IFAC Proc 37; 8: 2004; 716–721.
- Triggs B, McLauchlan PF, R I. Hartley, Fitzgibbon AW Bundle Adjustment — A Modern Synthesis. 2000; 298–372.
- Strasdat H, Montiel JMM, Davison AJ. Real-time monocular SLAM: Why filter? In 2010 IEEE International Conference on Robotics and Automation 2010; 2657–2664.
- Cui H, Shen S, Gao W, Wang Z. Progressive Large-Scale Structure-from-Motion with Orthogonal MSTs. In 2018 International Conference on 3D Vision (3DV) 2018; 79–88.
- Wang T, Lv G, Wang S, Li H, Lu B. SIFT Based Monocular SLAM with GPU Accelerated. In Lecture Notes of the Institute for Computer Sciences. Social-Informatics and Telecommunications Engineering, LNICST 237 LNICST 2018; 13–22.
- Bian J, Lin W. GMS : Grid-based Motion Statistics for Fast, Ultra-robust Feature Correspondence 4181–4190.
- Nie S, Jiang Z, Zhang H, Wei Q, Image matching for space objects based on grid-based motion statistics. 875 Springer Singapore 2018.
- Zhang X, Xie Z. Reconstructing 3D Scenes from UAV Images Using a Structure-from-Motion Pipeline. In 2018 26th International Conference on Geoinformatics. 2018; 2018:1–6.
- Yan K, Han M. Aerial Image Stitching Algorithm Based on Improved GMS. In 2018 Eighth International Conference on Information Science and Technology (ICIST) 2018; 351–357.
- Nobre F, Kasper M, Heckman C. Drift-correcting self-calibration for visual-inertial SLAM. In 2017 IEEE International Conference on Robotics and Automation (ICRA), 2017; 6525–6532.
- Mur-Artal R, Tardos JD. ORB-SLAM2: An Open-Source SLAM System for Monocular, Stereo, and RGB-D Cameras. IEEE Trans Robot 33; 5: 2017; 1255–1262.
- Shiozaki T, Dissanayake G. Eliminating Scale Drift in Monocular SLAM Using Depth From Defocus. IEEE Robot. Autom. Lett 3; 1:2018; 581–587.
- Muja M, Lowe DG. Fast approximate nearest neighbors with automatic algorithm configuration. VISAPP 2009 - Proc. 4th Int. Conf. Comput. Vis. Theory Appl., 1:2009; 331–340.
- Rublee E, Rabaud V, Konolige K, Bradski G. ORB: An efficient alternative to SIFT or SURF. In 2011 International Conference on Computer Vision. 2011; 2564–2571.
- Rosten E, Drummond T. Machine Learning for High-Speed Corner Detection. 2006; 430–443.
- Harris C, Stephens M. A Combined Corner and Edge Detector. in Procedings of the Alvey Vision Conference. 1988;1988: 69; 23.1-23.6.
- Kirkwood JR, Kirkwood BH. Elementary Linear Algebra. Chapman and Hall/CRC, 2017.
- Ourselin S, Roche A, Subsol G, Pennec X, Ayache N. Reconstructing a 3D structure from serial histological sections. Image Vis Comput 19; 1–2: 2001; 25–31.
- Beevers KR, Huang WH. SLAM with sparse sensing. In Proceedings 2006 IEEE International Conference on Robotics and Automation. 2006. ICRA 2006; 2006: 2006; 2285–2290.
- Sturm J, Engelhard N, Endres F, Burgard W, Cremers D. A benchmark for the evaluation of RGB-D SLAM systems. In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2012; 573–580.
- Mur-Artal R, Montiel JM M, Tardos JD. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot 31; 5: 2015; 1147–1163.
- Fossum ER. CMOS image sensors: electronic camera-on-a-chip. IEEE Trans Electron Devices 44;10: 1997; 1689–1698.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.


 Save to Mendeley
Save to Mendeley
