Trends in Computer Science and Information Technology
Central configurations of the circular restricted 4-body problem with three equal primaries in the collinear central configuration of the-3 body problem
Jaume Llibre*
Cite this as
Llibre J (2021) Central configurations of the circular restricted 4-body problem with three equal primaries in the collinear central configuration of the 3-body problem. Trends Comput Sci Inf Technol 6(1): 001-006. DOI: 10.17352/tcsit.000031In this paper we classify the central configurations of the circular restricted 4-body problem with three primaries with equal masses at the collinear configuration of the 3-body problem and an infinitisimal mass.
Introduction and results
The well-known Newtonian n-body problem concerns with the motion of n mass points with positive mass mi moving under their mutual attraction in Rd in accordance with Newton’s law of gravitation.
The equations of the motion of the n-body problem are
where we have taken the unit of time in such a way that the Newtonian gravitational constant be one, and ri€Rd (i=1…,n) denotes the position vector of the i-body, is the Euclidean distance between the i-body and the j-body.
The solutions of the 2-body problem (also called the Kepler problem) has been completely solved, but the solutions for the n-body for n>2, is still an open problem.
For the Newtonian n-body problem the simplest possible motions are such that the configuration formed by the n-bodies is constant up to rotations and scaling, such motions are called the homographic solutions of the n-body problem, and are the unique known explicit solutions of the n-body problem when n>2. Only some special configurations of particles are allowed in the homographic solutions of the n-body problem, called by Wintner [1] central configurations. Also, central configurations are of utmost importance when studying bifurcations of the hypersurfaces of constant energy and angular momentum, for more details see Meyer [2] and Smale [3]. These last years some central configurations have been used for different missions of the spacecrafts in the solar system, see for instance [4,5].
More precisely, let
be the total mass and the center of masses of the n bodies, respectively.
A configuration r=(r1,…,rn) is called a central configuration if the acceleration vectors of the n bodies are proportional to their positions with respect to the center of masses with the same constant λ of proportionality, i.e.
where λ is the constant of proportionality.
Equations (1) are strongly nonlinear and to find the explicit central configurations (r1,…,rn) in function of the masses m1,….mn when n>3 is an unsolved problem.
There is an extensive literature on the study of central configurations, see for instance Euler [6], Lagrange [7], Hagihara [8], Llibre [9,10], Meyer [2], Moeckel [11], Moulton [11], Saari [12], Smale [3], ..., and the papers quoted in these references.
In this paper we are interested in the planar central configurations of a circular restricted 4-body problem. Of course, for the central configurations of the 4-body problem there are many partial results, see for instance the papers [13-66].
We note that the set of central configurations is invariant under translations, rotations, and homothecies with respect their center of mass. It is said that two central configurations are equivalent if after having the same center of mass (doing a translation if necessary) we can pass from one to the other through a rotation around its common center of mass and a homothecy. This defines a relation of equivalence in the set of central configurations. From now on when we talk about a central configuration, we are talking on a class of central configurations under this relation of equivalence.
The objective of the present article is to study the central configurations of the circular restricted 4-body problem with three equal primaries in the collinear central configuration of the 3-body problem. We recall that for the 3-body problem when the three masses are equal there is a unique collinear central configuration, where the mass in the middle equidistant from the other two, of course the equal masses can be permuted in the positions of this configuration.
As in any circular restricted problem the objective is to describe the motion of the infinitesimal mass with respect to the primaries. Usually this problem is studied in a rotating system of coordinates where the positions of the primaries remain fixed, see for more details on the restricted problems the book of Szebehely [67].
More precisely, taking the unit of mass equal to the masses of the three primaries and since a central configuration is invarinat under rotations and homothecies through its center of mass without loss of generality we can assume that the position vector rj of the three primaries with masses m1= m2= m3= 1 are
We denote the position of the infinitesimal mass m4 = 0 by r4 = (x4,y4) = (x,y). Then our main result is the following one.
Theorem 1 The circular restricted 4-body problem with three primaries of equal masses m1= m2= m3= 1 with position vectors given in (2), and one infinitessimal mass m4 = 0 with position vector r4 =(x4,y4) =(x,y) have the following six central configurations with r4 = Pj for j=1 being:
(i) , where the value of the coordinate is a root of the polynomial ;
(ii) ;
(iii) , where the value of the coordinate is a root of the polynomial ;
(iV) , where the value of the coordinate is a root of the polynomial ;
(v) ;
(vi) .
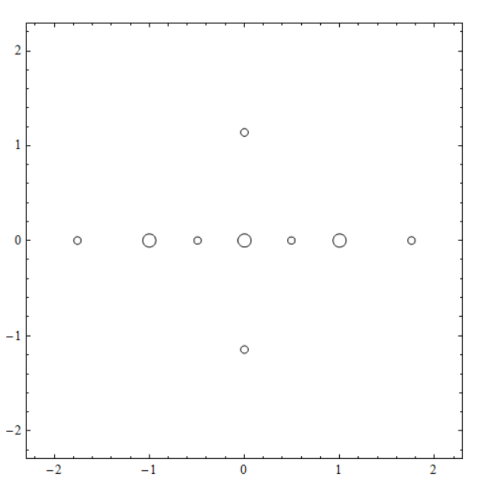
Figure 1.
The proof of Theorem 1 in given in the next section.
Proof of theorem 1
From (1) we obtain the following eight equations for the central configurations of the 4-body problem in the plane (3)
Where c= (c1, c2). Substituting in (3) the expressions (2), m1= m2= m3= 1, m4 = 0 and r4 =(x4,y4) =(x,y), corresponding to our circular restricted 4-body problem these eight equations reduce to
Therefore , and the position vector of r4 =(x4,y4) in order to have a central configuration of the circular restricted 4-body problem must be a real solution of the system
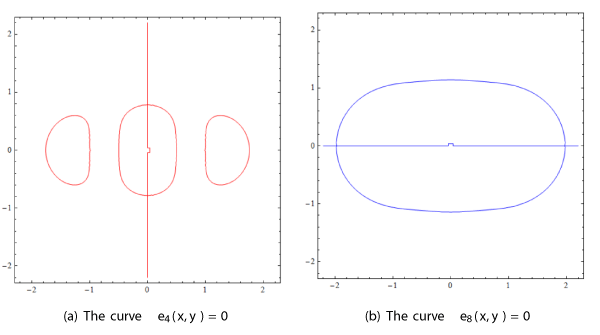
In Figure 2 we have shwon the curves e4 (x,y) =0 and e8 (x,y) =0, and in Figure 3 the intersection of these two curves. We see that these two curves intersect in six points inside the rectangle . Computing the coordenates of these six points numerically using the Newton method (see for instance [68]), we get the six points Pj which appear in the statement of Theorem 1. Of course we have omitted the three points where are located the three primaries in the intersections of the two curves e4 (x,y) =0 and e8 (x,y) =0, because there really these two curves are not defined. Now we shall prove that these six points obtained numerically really are solutions of the system e4 (x,y) =0 and e8 (x,y) =0.
We note that equations e4 (x,y) =0 and e8 (x,y) =0 are invariant if we change x by -x, and y by -y, so if (x,y) is a solution of the system e4 (x,y) =0 and e8 (x,y) =0, also (-x,y), (x, -y) and (-x,-y) are solutions. So in order to prove Theorem 1 we only need to study the solutions of system e4 (x,y) =0 and e8 (x,y) =0 satisfying and . Moreover, from Figure 3 we see that all the solutions are of the form (x,0) or (0,y), and since in the origin (0,0) there is one primary, we must look only for the solutions (x,0) or (0,y) with x > 0 and y> 0.
First we look for the solutions (0,y) with y>0, then system e4 (x,y) =0 and e8 (x,y) =0 reduce to
or equivalently to
Squaring the both sides of the this equation we get the equation
This polynomial equation has only two real roots
but only the second root satisfies equation (4). This provides the solution P1 of Theorem 1, and consequently also the solution P2.
Now we look for the solutions (x,0) with (x>0) of the system e4 (x,y) =0 and e8 (x,y) =0. For these solutions the system reduce to
squaring the both sides of the previous equality we obtain
Writting this equation with a common denominator, which only vanishes at the positions of the primeries, its numerator equal zero can be written as
Squaring again the both sides of the this equality we get
The real zero x = 1 is not good because it correspond to the position of a primary. The unique real root of the polynomial -4+5x3-12x4-10x5+5x7 is 1.7576799791694022.. which also is a zero of equation (5), and consequently provides the central configuration P3, and by the symmetries of the equations of the central configurations also provides the central configuration P6.
The unique real root of the polynomial -4+8x2+21x3-4x4-10x5+5x7 is 0.4946664910171345… which also is a zero of equation (5), and consequently provides the central configuration P4, and due to the symmetries of the equations of the central configurations also provides the central configuration P5.
The real roots of the polynomials -4+8x2-11x3-4x4-10x5+5x7 and 4+16x2+5x3+4x4-10x5+5x7 are not zeros of the equation (5). This completes the proof of Theorem 1.
The first author is partially supported by the Ministerio de Ciencia, Innovación y Universidades, Agencia Estatal de Investigación grants PID2019-104658GB-I00 (FEDER), the Agència de Gestió d’Ajuts Universitaris i de Recerca grant 2017SGR1617, and the H2020 European Research Council grant MSCA-RISE-2017-777911.
- Wintner A (1941) The Analytical Foundations of Celestial Mechanics, Princeton University Press. Link: https://bit.ly/3n7ci8v
- Meyer KR (1987) Bifurcation of a central configuration. Celestial Mech 40: 273-282. Link: https://bit.ly/3o7RcIl
- Smale S (1970) Topology and mechanics II: The planar n–body problem. Inventiones math 11: 45-64. Link: https://bit.ly/3rNgltW
- Gómez G (2001) Dynamics and Mission Design Near Libration Points. Vol. I Fundamentals: The case of collinear libration points, World Scientific Monograph Series in Mathematics 2. Link: https://bit.ly/387zjUc
- Gómez G (2001) Dynamics and Mission Design Near Libration Points. Vol. I Fundamentals: The case of collinear libration points, World Scientific Monograph Series in Mathematics 2. Link: https://bit.ly/387zjUc
- Euler L (1767) De moto rectilineo trium corporum se mutuo attahentium. Novi Comm Acad Sci Imp Petrop 11: 144-151. Link: https://bit.ly/38S8Jhg
- Lagrange JL (1873) Essai surle probleme des trois corps, recueil des pieces qui ont remporte le prix de l’Academie royale des Sciences de Paris,tome IX, 1772, reprinted in Ouvres 6: 229–324.
- Hagihara Y (1970) Celestial Mechanics. 1. MIT Press, Massachusetts.
- Llibre J (1991) On the number of central configurations in the n-body problem. Celestial Mech Dynam Astronom 50: 89-96. Link:
- Llibre J (2017) On the central configurations of the n-body problem. Appl Math Nonlinear Sci 2: 509-518. Link: https://bit.ly/2JHHBZS
- Moeckel R (1990) On central configurations. Math Zeitschrift 205: 499-517. Link: https://bit.ly/3hM34xr
- Saari DG (1980) On the role and properties of central configurations. Celestial Mech 21: 9-20. Link: https://bit.ly/3862ZRV
- Albouy A (1995) Symetrie des configurations centrales de quatre corps. CR Acad Sci Paris 320: 217-220. Link: https://www.semanticscholar.org/paper/Sym%C3%A9trie-des-configurations-centrales-de-quatre-Albouy/4408d2a8d129b375cc5eae706f6ddc5583a238e1
- Albouy A (1995) The symmetric central configurations of four equal masses, Hamiltonian dynamics and celestial mechanics (Seattle, WA, 1995). 131–135, Contemp. Math. 198, Amer. Math. Soc., Providence, RI, 1996. Link:
- Albouy A, Fu Y, Sun S (2008) Symmetry of planar four body convex central configurations. Proc R Soc Lond Ser A Math Phys Eng Sci 464: 1355-1365. Link: https://hal.archives-ouvertes.fr/hal-00153212
- Albouy A, Kaloshin V (2012) Finiteness of central configurations of five bodies in the plane. Ann Math 176: 535-588. Link: https://annals.math.princeton.edu/2012/176-1/p10
- lvarez-RamÃrez M, Corbera M, Delgado J, Llibre J (2004) The number of planar central configurations for the 4-body problem is finite when 3 mass positions are fixed. Proc Amer Math Soc 133: 529-536. Link: https://bit.ly/3pLCMOx
- lvarez-RamÃrez M, Delgado J (2003) Central configurations of the symmetric restricted 4-body problem. Celestial Mech Dynam Astronom 87: 371-381. Link: https://bit.ly/3b0YhGM
- lvarez-RamÃrez M, Llibre J (2013) The symmetric central configurations of the 4-body problem with masses. Appl Math Comp 219: 5996-6001. Link: https://bit.ly/3pBge2E
- lvarez-RamÃrez M, Llibre J (2018) Hjelmslev quadrilateral central configurations. Physics Letters A 383: 103-109. Link: https://bit.ly/3pA85eW
- lvarez-RamÃrez M, Llibre J (2019) Equilic quadrilateral central configurations. Commun Nonlinear Sci Numer Simul 78: 104872. Link: https://bit.ly/3hyuiHw
- Alvarez-Ramirez A, Santos AA, Vidal C (2013) On co-circular central configurations in the four and five body-problem for homogeneous force law. J Dynam Differential Equations 25: 269-290. Link: https://bit.ly/3ob5Tui
- Arribas M, Abad A, Elipe A, Palacios M (2016) Equilibria of the symmetric collinear restricted four-body problem with radiation pressure, Astrophys. Space Sci 361: 12. Link: https://bit.ly/38UNfAe
- Arenstorf RF (1982) Central configurations of four bodies with one inferior mass. Cel Mechanics 28: 9-15. Link: https://bit.ly/3aWsRBv
- Barros JF, Leandro ESG (2011) The set of degenerate central configurations in the planar restricted four-body problem. SIAM Journal on Mathematical Analysis 43: 634-661. Link: https://bit.ly/3hyufvk
- Barros JF, Leandro ESG (2014) Bifurcations and enumeration of classes of relative equilibria in the planar restricted four-body problem. SIAM Joural on Mathematical Analysis 46: 1185-1203. Link: https://bit.ly/3pK1aQi
- Bernat J, Llibre J, Perez-Chavela E (2009) On the planar central configurations of the 4-body problem with three equal masses. Dyn Contin Discrete Impuls. Syst Ser A Math Anal 16: 1-13.
- Chenciner A (2017) Are nonsymmetric balanced configurations of four equal masses virtual or real?. Regul Chaotic Dyn 22: 677-687. Link: https://bit.ly/3rIlWBQ
- Corbera M, Cors JM, Llibre J, Perez-Chavela E (2019) Trapezoid central configurations. Appl Math Comput 346: 127-142. Link: https://bit.ly/3n5WCSW
- Corbera M, Llibre J (2014) Central configurations of the 4-body problem with masses m1=m2>m3=m4=m>0 and m small. Appl Math Comput 246: 121-147. Link: https://bit.ly/2MpY0Dc
- Corbera M, Cors JM, Llibre J (2011) On the central configurations of the planar -body problem. Celestial Mech Dynam Astronom 109: 27-43.
- Corbera M, Cors JM, Roberts GE (2018) A four-body convex central configurationGwith perpendicular diagonals is necessarily a kite. Qual Theory Dyn Syst 17: 367-374. Link: https://bit.ly/3bdf8GL
- Corbera M, Cors JM, Roberts GE (2019) Classifying four-body convex central configurations. Celestial Mech Dynam Astronom 131: 34. Link: https://bit.ly/3hykFst
- Cors JM, Roberts GE (2012) Four-body co-circular central configurations. Nonlinearity 25: 343-370. Link: https://bit.ly/2MrdKG0
- Cors JM, Llibre J, Ollé M (2004) Central configurations of the planar coorbital satellite problem. Celestial Mech Dynam Astronom 89: 319-342. Link: https://bit.ly/2LhG1hO
- Deng Y, Li B, Zhang S (2017) Four-body central configurations with adjacent equal masses. J Geom Phys 114: 329-335. Link: https://bit.ly/38LAI1S
- Deng Y, Li B, Zhang S (2017) Some notes on four-body co-circular central configurations. J Math Anal Appl 453: 398-409. Link: https://bit.ly/3hxqo1I
- Deng C, Zhang S (2014) Planar symmetric concave central configurations in Newtonian four-body problems. J Geom Phys 83: 43-52. Link: https://bit.ly/3pMVwgF
- Rdi B, Czirj KZ (2016) Central configuration of four bodies with an axis of symmetry. Celestial Mech Dynam Astronom 125: 33-70. Link: https://bit.ly/2MqBEkZ
- Fernandes AC, Llibre J, Mello LF (2017) Convex central configurations of the 4-body problem with two pairs of equal masses. Arch Rational Mech Anal 226: 303-320. Link: https://bit.ly/38O6FXw
- Gannaway JR (1981) Determination of all central configurations in the planar 4-body problem with one inferior mass, Ph. D., Vanderbilt University, Nashville, USA.
- Fernandes AC, Garcia BA, Llibre J, Mello LF (2018) New central configurations of the (n+1) body problem. J Geom Phys 124: 199-207. Link: https://bit.ly/3rL2K6m
- Grebenikov EA, Ikhsanov EV, Prokopenya AN (2006) Numeric-symbolic computations in the study of central configurations in the planar Newtonian four-body problem, Computer algebra in scientific computing, 192–204. Lecture Notes Comput Sci. Link:
- Hampton M (2003) Co-circular central configurations in the four-body problem. EQUADIFF 993–998. Link: https://bit.ly/38Wj63F
- Hampton M, Moeckel R (2006) Finiteness of relative equilibria of the four-body problem. Invent Math 163: 289-312. Link: https://bit.ly/34YmsSj
- Hassan MR, Ullah MS, Aminul HM, Prasad U (2017) Applications of planar Newtonian four-body problem to the central configurations. Appl Appl Math 12: 1088-1108. Link: https://bit.ly/3hycLiP
- Leandro ESG (2006) On the central configurations of the planar restricted four-body problem. J Differential Equations 226: 323-351. Link: https://bit.ly/3o8Wovk
- Llibre J (1976) Posiciones de equilibrio relativo del problema de 4 cuerpos. Publicacions Matemàtiques UAB 3: 73-88. Link: https://bit.ly/2KMCZCi
- Llibre J, Yuan P (2019) Bicentric quadrilateral central configurations. Appl Math Comput 362: 124507. Link: https://bit.ly/3rLKyK0
- Llibre J, Yuan P (2020) Tangential trapezoid central configurations. Regul Chaotic Dyn 25: 651-661. Link: https://bit.ly/2X3F6nG
- Long Y (2003) Admissible shapes of 4-body non-collinear relative equilibria. Adv Nonlinear Stud 3: 495-509. Link: https://bit.ly/387q5rc
- Long Y, Sun S (2002) Four-Body Central Configurations with some Equal Masses. Arch Ration Mech Anal 162: 25-44. Link: https://bit.ly/3b89Zzk
- MacMillan WD, Bartky W (1932) Permanent Configurations in the Problem of Four Bodies. Trans Amer Math Soc 34: 838-875. Link: https://bit.ly/2X3EYVe
- Ouyang T, Xie Z (2005) Collinear central configuration in four-body problem. Celestial Mech Dynam Astronom 93: 147-166. Link: https://bit.ly/3hzJPqA
- Pedersen P (1944) Librationspunkte im restringierten Vierkörperproblem. Danske Vid Selsk Math Fys 21: 1-80. Link: https://bit.ly/3b1ftMA
- Perez-Chavela E, Santoprete M (2007) Convex four-body central configurations with some equal masses. Arch Rational Mech Anal 185: 481-494. Link: https://bit.ly/3naQzMB
- Pina E (2013) Computing collinear 4-body problem central configurations with given masse. Discrete Contin. Dyn Syst 33: 1215–1230. Link: https://bit.ly/38UbE9e
- Pina E, Lonngi P (2010) Central configuration for the planar Newtonian four-body problem. Celest Mech Dyn Astron 108: 73-93. Link: https://bit.ly/2LdRAWW
- Rusu D, Santoprete M (2016) Bifurcations of central configurations in the four-body problem with some equal masses. SIAM J Appl Dyn Syst 15: 440-458. Link: https://bit.ly/2KWIGgK
- Shi J, Xie Z (2010) Classification of four-body central configurations with three equal masses. J Math Anal Appl 363: 512-524. Link: https://bit.ly/2LdKiTn
- Shoaib M, Kashif AR, Szücs-Csillik I (2017) On the planar central configurations of rhomboidal and triangular four- and five-body problems. Astrophys Space Sci 362: 182. Link: https://bit.ly/2L7l4G5
- Simo C (1978) Relative equilibrium solutions in the four-body problem. Cel Mechanics 18: 165-184. Link: https://bit.ly/3pFMbXJ
- Tang JL (2006) A study on the central configuration in the Newtonian 4-body problem of celestial mechanics (Chinese). J Systems Sci Math Sci 26: 647-650.
- Xie Z (2012) Isosceles trapezoid central configurations of the Newtonian four-body problem. Proc Roy Soc Edinburgh Sect A 142: 665-672. Link: https://bit.ly/3o6LlD5
- Yoshimi N, Yoshioka A (2018) 3+1 Moulton configuration. SUT J Math 54: 173-190.
- Herget P (1967) Theory of orbits, The restricted problem of three bodies, Academic Press, New York. Link: https://bit.ly/3n7ki9a
- Bernat J, Llibre J, Perez-Chavela E (2009) On the planar central configurations of the 4-body problem with three equal masses. Dyn Contin Discrete Impuls. Syst Ser A Math Anal 16: 1-13.
- Stoer J, Bulirsch R (1980) Introduction to numerical analysis, Springer-Verlag, New York. Link: https://bit.ly/3521NNi
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.


 Save to Mendeley
Save to Mendeley
