Open Journal of Cell and Protein Science
The DNA conformational energy landscape: sequence-dependent conformational equilibria of duplex DNA
Karim M ElSawy1,2* and Leo SD Caves3
2Department of Chemistry, College of Science, Qassim University, Saudi Arabia
3Independent Researcher and Associate of the York Cross-Disciplinary Centre for Systems, Analysis, University of York, United Kingdom
Cite this as
ElSawy KM, Caves LSD (2020) The DNA conformational energy landscape: sequence-dependent conformational equilibria of duplex DNA. Open J Cell Protein Sci 3(1): 001-010. DOI: 10.17352/ojcps.000002The free energy surfaces of duplex dinucleotide steps were mapped in a principal conformational subspace derived from crystal structure data on DNA duplex oligomers. The three dimensional subspace, spanned by collective degrees of freedom representing linear combinations of the Cartesian coordinates of the backbone and sugar atoms of both strands accounted for 77% of the total variance of the observed structural distribution. The features of the subspace free energy surface correspond well to the distribution of observed structures exhibiting a clear separation of A- and B-family classes. The sequence dependence of the relative A / B-form conformational equilibria was derived from the corresponding subspace free energy surfaces at physiological conditions. A B-philicity scale representing the mole fraction of the BI-form vs the A-family for the 10 unique dinucleotide steps revealed three classes of sequences: highly B-philic (GC/GC & CG/CG), B-philic (AC/GT, AA/TT, AT/AT, CA/TG, AG/CT & GG/CC) and A-philic (GA/TC & TA/TA). The high propensity of the TA/TA step to adopt the A-form conformation is in accord with single crystal X-ray diffraction data and has biological significance in view of the frequent presence of the TATA sequence motif in transcriptional promoter regions.
Introduction
There have been several attempts to explore the conformation and energetics of DNA, using a variety of both backbone torsion angles and helicoidal parameters as effective degrees of freedom [1-6]. Several approximations were made to overcome the problem of dealing with a large number of degrees of freedom. For example, in a study of the energetics of base stacking [7], the backbone was replaced with methyl groups at the C1´ atoms. Using this model, the values of base-step parameters were predicted accurately provided that the values of slide, shift and propeller were assigned to observed values. In a subsequent study [8], a C1´- C1´ virtual bond model was combined with two helical degrees of freedom, slide and shift, to compute the potential energy surface of an isolated dinucleotide step. In this model, the position of the low energy regions agreed well with the geometry of observed crystal structures, but for only some of the base steps. For other base steps, the lack of agreement of energy landscape with the observations was ascribed to the neglect of the effects of conformational coupling with neighbouring steps (context dependence).
Therefore, in many studies of DNA conformation, the backbone is considered as a passive element that delineates the boundaries of the dinucleotide step [9] such that it acts as no more than a constraint on the range of the conformational space accessible to the bases [10]. However, the growing evidence of the biological significance of DNA conformational states other than the B-form [11,12] with regard to DNA packaging [13], transcription [14-16], spore UV resistance [17] and protein recognition [11,12,18-20], signals the importance of backbone conformational flexibility. We reaffirmed the importance of backbone conformation to DNA structure by revealing that steric interactions within the backbone of the single strand are key determinants of the conformational preferences of duplex DNA [21].
Moreover, ions are known to play an important role in the conformation of oligomeric DNA structures by shielding the phosphate charges and affecting water activity around DNA [22-24]. In this respect, the conformational equilibria of DNA are highly sensitive to the salt concentration, such that A‑form DNA is found in solutions with 1 M salt concentrations and above, whereas at lower concentrations, B-DNA is usually prevalent [25,26]. This conformational change is not only dependent on the environment, but it is also strongly dependent on the sequence of the base pairs [27]. Given the importance of the different conformational states of DNA to its biological function, it is of interest to examine their characteristics at physiological conditions.
In this study, we extend the methodology established in our previous works [21,28] to map and characterise the free energy surface (FES) of duplex Dinucleotide Steps (DS) within a Principal Conformational Subspace (PCS) derived from dinucleotide steps observed in duplex crystal structures. A key feature of this work (Focussing on the duplex FES) is the use of collective degrees of freedom based on linear combinations of the Cartesian coordinates of the backbone and sugar atoms in order to account for the inter-strand interactions which were absent from the single strand PES [21]. In doing so, a more sophisticated model of the electrostatic effects is employed at near physiological conditions i.e. in water with a salt concentration of 0.15 M and a temperature of 298 K.
The structural, energetic and thermodynamic characteristics of the duplex FES are discussed and compared in terms of the location and relative stability of different local energy minima. Validation of the fidelity of the FES is presented by considering the relationship of its features with experimentally observed crystal structure distributions within the PCS. The utility of the FES is illustrated via calculation of a B-philicity scale for the ten dinucleotide steps based on the corresponding free energy surfaces within the PCS at physiological conditions. The derived B-philicity scale is then compared to known experimental and theoretical trends.
Data and methods
Conformational descriptors
The Cartesian coordinates corresponding to the atoms comprising the backbone and sugar torsions of both strands were used to describe the conformational space of duplex dinucleotide steps. This atom subset is common for the ten unique dinucleotide steps [9]. For the subset of 42 atoms, a total of 126 Cartesian (X,Y,Z) coordinates is used to describe each dinucleotide step (Figure 1).
We note that the use of a Cartesian coordinate representation in this work, rather than a torsion angle representation (which was used in our previous work [21]), accounts for both the inter-strand and intra-strand conformational variation and naturally incorporates both the backbone conformation and the inter-base pair orientation. Accounting for these degrees of freedom in a torsion angle space is difficult as it requires a large number of torsion angles along with a definition of the inter-strand distance. Using a mixture of backbone torsions and helical parameters is less convenient as it incorporates different units (Ǻ and degrees) into the basis set which necessitates standardization of variables [29,30]and complicates the methodology. Use of a Cartesian space representation circumvents the problems of periodicity in the torsion angle representation [31].
Data acquisition
Structural data were obtained from the Nucleic Acid Database [32] (http://ndbserver.rutgers.edu). Crystal structures of duplex A-DNA and B‑DNA were selected which met the following criteria: high resolution (dmin< 2.5 Å); containing no base-mismatches or chemical modifications and those that are not in complex with drugs or proteins. Z‑DNA was not included due to the paucity of structural data meeting the selection criteria. As in other studies [33], we regard different crystalline environments for the same sequence as distinct observations. From the sample of structures meeting these criteria (Supplementary Material, Table 1), the conformational descriptors (described above) were assembled in an n × p data matrix (M) in a row wise fashion, where n is the number of dinucleotide steps in the sample (n=675) and p is the number of coordinates per step (p=126).
Data preparation
Analysing sets of different structures described by Cartesian coordinates requires establishing a common spatial reference frame, which was achieved by superposition onto a single template structure. The template structure used was the unweighted geometric mean structure: A distance matrix (D) for each row of the matrix M was generated such that Dij corresponds to the Euclidian distance between atom i and atom j within the same dinucleotide step. An average distance matrix (DD) was then calculated such that DDij corresponds to the average distance between atom i and atom j calculated over all corresponding entries in the D matrices. The matrix DD was subjected to principal coordinate analysis [30] to provide a three dimensional embedding corresponding to the (Cartesian coordinates of the) template structure. It is noted that generating the template structure in this way has the advantage that it is reference frame independent [34]. All of the dinucleotide structures (rows in the data matrix M) were then superposed on the template structure using the least squares algorithm of Kabsch [35,36]. Coordinate superposition was performed on all 42 atoms using equal weights. All subsequent analysis is performed on the superposed data matrix (R).
Multivariate analysis
Principal component analysis: Principal component analysis (PCA) was performed in order to exploit the intrinsic covariance structure of the data matrix to effect a dimensionality reduction [30]. The eigenvectors (principal components or PCs) can be considered as collective degrees of freedom that form an orthogonal basis set for describing the dinucleotide step (DS) conformational distribution via concerted Cartesian coordinate displacements from the mean structure. The corresponding eigenvalues represent the variance of the conformational distribution along each of the collective degrees of freedom. The extent to which a given observation lies along the kth principal component is given by the projection . These projections (or scores) may be used for visualising the distribution of observatiosns in the principal conformational subspace of the dinucleotide steps.
Cluster analysis: The scores along the first three principal components were split into two classes following the NDB classification of A‑form and the B-form structures from which the data were derived. Each of these classes was subjected separately to hierarchical clustering using the Ward linkage method [37]. This resulted in 3 clusters for the A-form category and 5 clusters for the B-form category. The whole dataset was then subjected to non-hierarchical k-means clustering [38], seeded using the centroids of the 8 clusters obtained from the previous step. A Euclidean metric was used throughout [39].
Empirical energy calculations
Mapping the Potential Energy Surface (PES) (in vacuum): The vacuum potential energy was calculated at each grid point in a manner very similar to that discussed in our previous work [21] apart from minor changes. For the sake of completeness and clarity we describe it again. The potential energy surface of the ten unique (duplex) dinucleotide steps within the PCS was mapped via systematic energy evaluation on a grid defined by discrete points along the first three PCs. The subspace coordinates of a grid point correspond to a set of Cartesian coordinates, . Therefore, the coordinates xi, correspond to a structure reconstructed in the 3D subspace whose projections along higher principal components are set to zero. The potential energy was calculated using the AMBER force field [40], using the Cornell parameterisation [41], implemented in the CHARMM program [42]. No non-bonded interaction truncation was performed. A grid resolution of 0.5 Å in the (PC1, PC2, PC3) subspace was used over the range ‑12 to 12 Å (corresponding to a range of conventional RMSD of -1.85 to 1.85 Å) with respect to an origin corresponding to the mean structure. These search limits were chosen so as to encompass the range of scores spanned by the superposed data matrix (R). The position of the atoms corresponding to the PCA basis were restrained to maintain the desired PCS projection using a harmonic penalty function with a force constant of 50 kcal mol‑1 Å‑2 and the system was energy minimised using the steepest descent (200 steps) followed by 2000 steps using ABNR method of CHARMM [42]. Characterisation of the features of the FES and calculation of the thermodynamic equilibria between different forms was conducted via estimation of the local partition function of each energy valley as described previously [21].
Calculation of the electrostatic component of the solvation free energy (∆Aelec)
The electrostatic component of the solvation free energy was calculated by solving the linearized Poisson-Boltzmann (PB) equation for the structures corresponding to each of the subspace grid points after minimization using a finite difference (FDPB) algorithm [43] implemented in the PBEQ module [44] of CHARMM. The electrostatic component of the solvation free energy ∆Aelec was obtained from the difference between the electrostatic potential computed in bulk solvent (salt concentration = 0.15 M, relative dielectric permitivity = 80) and the electrostatic potential calculated in vacuum (salt concentration = 0.0 M, relative dielectric permitivity = 1.0) at 298 K. The relative dielectric permittivity of the solute was set to 1 consistent with the use of a non-polarizable force field and a fixed solute conformation [45]. The solute-solvent boundary was constructed from the solvent accessible surface using a solvent probe radius of 1.4 Å. To improve the accuracy of the FDPB calculations the ‘focusing’ technique [46] was used. The FDBP calculations were designed as to immerse all the subspace structures in a final grid of 0.4 Å spacing which extends 6 Å from the edge of the molecule in each direction (x, y and z). This was conducted as follows: Each subspace grid structure was reoriented to its principal axes; an initial grid which extends 12 Å from the edge of the molecule in each direction was then constructed with initial grid spacing of 0.8 Å. The atomic partial charges were distributed over the nearest eight grid points using trilinear interpolation and an initial solution of PB equation was obtained using this charge distribution. The grid spacing was then decreased by 0.066 Å and the distance from the edge of the solute in each direction (X axis, Y axis and Z axis) was decreased by 1 Å where the boundary potential was set using the known potential from the previous step. This process was repeated 6 times until a final grid spacing of 0.4 Å was reached.
The Free Energy Surface (FES)
Calculation of the total solvation free energy can be visualized as a two step process; first formation of an uncharged (non-polar) solvent cavity and second charging the solute in solution [47]. This divides the total free energy of solvation into two contributions; non-polar and electrostatic. For charged systems like DNA the second of these contributions predominates. Also, the entropic contributions to the total free energy resulting from the fluctuations of the free degrees of freedom of the dinucleotide steps at each grid point is expected to be minimal since we restrain most of the system’s degrees of freedom. Therefore, only the electrostatic component was considered in this work. The electrostatic solvation free energy component (∆Aelec) of each grid point was added to the vacuum potential energy surface in order to obtain a free energy surface (FES) which incorporates the salt and solvation effects at near physiological conditions.
Conformational preferences of dinucleotide steps (a B-philicity scale)
The B-philicity of each dinucleotide step was represented by the equilibrium concentration of the BI-form vs. the A-family at physiological conditions in terms of the mole fraction of the BI-form. The calculation of the mole fraction was based on estimation of the local partition functions within the energy valleys of the A and BI-forms (QA and QBI respectively) as described previously [21]. We note that our consideration of local energy valleys (rather than just energy minima) naturally incorporates the contribution of conformational entropy to their relative free energy differences. The BI-form mole fraction () can be expressed in terms of the relative free energy difference of the BI and A forms () as follows:
Results and discussion
The principal conformational subspace (PCS)
Characterisation of the PCS: The eigenvalues resulting from diagonalization of the covariance matrix of the mean-centred superposed data matrix represent the amount of variance captured along each of the corresponding eigenvectors (or principal components) [30]. The relative contribution of the (sorted) eigenvalues to the total variance levels off after the third or fourth principal component and the distributions of scores along the fourth, fifth and six principal components are unimodal and therefore do not contribute significantly to additional clustering of the data (results not shown). The first principal component accounts for 54.4 % of the variance, the second accounts for 14. 7 % while the third accounts for almost 8 %, details about the geometric character of the principal components are provide in Supplementary Material. Therefore, the first three principal components, which collectively describe almost 77 % of the total variance, were used as the basis set, spanning the PCS of the sample of dinucleotide steps, in the subsequent mapping of the free energy surface. For the interpretation of the principal components (eigenvectors) in terms of concerted atomic displacements [48], see Supplementary Material.
The Free Energy Surface within the PCS
The FESs of all ten possible sequences for dinucleotide steps were computed in the PCS, however here we present that for a CA/TG step (Figure 2 left panel) as an example. Three low energy regions on the FES are readily apparent from visual examination. A quantitative partitioning of the FES [21] confirmed the presence of three distinct energy valleys that were then analysed individually in terms of their structural and energetic characteristics.
Structural characterization of the low energy valleys of the FES
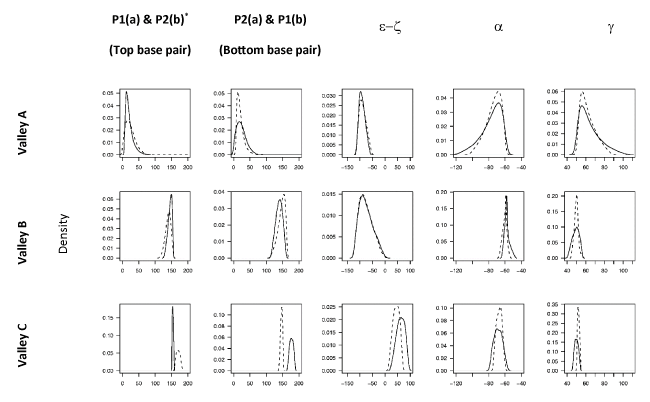
Profiles of the backbone structural parameters for both strands of the DS in each of the three energy valleys on the FES are shown in Figure 3. We adopted a binary‑state classification scheme for the DS embracing the fact that the conformational states of the individual strands need not be the same [49], e.g. BI.BII denotes a DS structure in which one of the strands is in the BI form while the other is in the BII form. (NB: we consider state X.Y as equivalent to Y.X). In accord with the character of the underlying collective coordinates (see above), we found that PC1 serves to discriminate the valleys corresponding to the A and B-family conformers. The geometric characteristics of both strands (with regard to sugar puckers and e/z torsion ranges) of the structures within Valley B and C (see Figure 2a) are similar and are found to correspond to the ranges of the BI-form and BII-form respectively (Figure 3) leading to a classification of the BI.BI and BII.BII states. The geometric characteristics of Valley A (e.g. sugar puckers in the C3´-endo range – see Figure 3) reveal that it corresponds to structures within the A-family. However, both a and g torsions show broad distributions for both strands which tail towards regions corresponding to the crankshaft A-form (CrA). Thus structures within Valley A show a fairly continuous spectrum of conformational states ranging from the A.A to the CrA.CrA states.
The presence of the A-family conformational states within a single energy valley (Valley A) suggests a loss of fine topographical details within this region of the FES. The compact nature of the A-form family structures relative to their counterparts in the B-family mitigates against their representation in the 3D PCS representation. These fine details can be recovered by extending the representation to higher dimensions, or alternatively by performing separately PCA on A and B-form structures. An example of the latter approach, showing an A-form PCS, which shows better separation of the A-form substates and distinct minima on the corresponding PES is provided in Supplementary Material.
Relative energetics of the valleys on the FES
The location and relative energetics of the lowest local energy minima within the energy valleys for the ten unique dinucleotide steps [9] are given in Table 1. The relative energies of valley A and B minima (ΔEBI-A) depend sensitively on the sequence of the dinucleotide step. Except for the GG/CC, GA/TC and the TA/TA steps, valley B (BI.BI states) contains the global energy minimum. The variation of the relative free energy difference between the two valleys (ΔABI-A) does not always follow the trend of the ΔEBI-A values due to the varying entropic contribution (see TΔSBI-A values) which is almost 66% of the ΔEBI-A value in case of the GA/TC step. The positive values of the TΔSBI-A are consistent with the known flexibility of the BI-form relative to the A-form and reflects the importance of entropic factors in stabilizing the BI-form relative to the A-form. This is consistent with our previous results [21] (based on single strand dinucleotide PES) that the bias towards the BI-form relative to the A-form is not only due to enthalpic factors but also due to entropic factors.
Valley C (BII.BII states), if present, corresponds to the highest energy minimum and the shallowest valley with the smallest volume (data not shown). Accordingly, in this context, given the lack of enthalpic or entropic stabilisation, the BII.BII states may be termed metastable. A similar view of the BII conformation emerged in our previous work on the PES of single strand dinucleotide monophosphate models (ElSawy, 2005 #513). In this context we noted the suggestions by other workers that the observation of the BII conformation in crystal structures may be a result of packing effects [50,51].
Validation of the FES
An important step in validating the computed FES is to compare its fidelity with respect to certain observed structural properties of DNA.
Distribution of observed structures on the subspace FES
Each observation in the data matrix (containing sample DS from crystal structures of the A-DNA and B-DNA families) was pre-classified into known DNA conformational forms A, CrA (Crank-A), BI, and BII using relevant backbone torsion angle ranges [52-54]. Projection of the observations into the PCS results in pronounced clustering into the low energy regions on the FES (Figure 2b). Only six binary substates were identified in our data namely A.A, A.CrA, CrA.CrA, BI.BI, BI.BII and BII.BII, representing a mixing of substates within the A or B families (Table 2). It is notable that substates of both A and B families are not found in the same dinucleotide step (see Table 2) i.e. the different families appear to be mutually exclusive within the context of an individual DS.
Projection of the data onto the FES (Figure 2b) reveals that the A-family substates are well separated from those of the B-family. However, the three binary states of the A-family appear to exist within the same energy valley (Valley A) i.e. we do not observe energy barriers between these states on the FES in the 3D PCS (see Figure 3); these regions do appear in separate energy valleys in a principal conformational subspace which comprises only the A-form family (see Supplementary Material).
On the other hand, the separation of the B-family substates is more pronounced than within the A-family. In the PC1-PC3 plane, complete separation of BII.BII structures into Valley C (BII.BII states) is observed (Figure 2b). The BI.BI and BI.BII structures are slightly overlapped, however the BI.BI structures project into the bottom of Valley B (BI.BI states) while the density of the BI.BII structures increases in the direction of Valley C. Furthermore, it is noted that Valleys B and C are parts of a larger energetic basin which encompasses the B-family substates and separates them from those of the A family. We note that the position of the BI.BII substate in relation to the BI.BI, and BII.BII substates is highly suggestive that interconversion between the BI.BI and the BII.BII states proceeds on a strand-wise basis.
Utility of the FES
The utility of the FES is illustrated by the derivation of a realistic B-philicity scale which reflects the conformational behaviour of the dinucleotide steps at near physiological conditions. The B-philicity scale is based on a statistical thermodynamical estimation of the local partition functions of the local energy valleys within the subspace free energy surface (see Methods). This physical approach is distinct from existing statistical approaches which infer A and B- forms propensities from databases of structures determined under a variety of experimental conditions e.g. [55].
A relative B-philicity scale for dinucleotide steps
The B-philicity (tendency to be in the BI-form vs the A-family) of isolated (i.e. non-oligomeric) DNA dinucleotide steps (as indicated by the ∆ABI-A values and the mole fraction of BI-form structures in Table 1) reveals that, as expected, for most of the dinucleotide steps, the B-form is predominant at physiological conditions [56]. However, under these conditions (conventionally associated with the B-form) we find that the GA/TC and TA/TA steps favour the A-form.
In terms of the total free energy difference between the BI-form and A-form (∆ABI-A), the ten dinucleotide steps can be divided into three categories; highly B-philic (GC/GC & CG/CG), B-philic (AC/GT, AA/TT, AT/AT, CA/TG, AG/CT & GG/CC) and A-philic (GA/TC & TA/TA). In the following we compare this trend with available theoretical and experimental data. In doing this, we need to carefully consider the nature of the systems and environments in the experiments, against the nature of our theoretical model which represents isolated dinucleotide steps (i.e. without oligomeric neighbour/context effects) in low salt (0.15 M) aqueous solution at 298 K.
Highly B-philic: GC/GC & CG/CG steps
GC/GC & CG/CG steps show the largest free energy differences ∆ABI-A indicating that these steps are highly B-philic. The high preference for the B-form by the CG step is in accord with the crystallographic observation that the single dinucleotide duplex structure of d(CG)2 exists in the B-form in aqueous solutions ranging from 0.1 to 1.0 M NaCl in a temperature range from 273 to 298K [57]: the B-form conformation was found even in high salt solutions (5.0-6.0 M NaCl). Thus our computed high B-philicity of the CG/CG step (∆ABI-A= -1.74 kcal/mol, see Table 1) is in accord with a study where the length of the duplex structure and the experimental conditions are a good general match with our model.
Solution circular dischroism studies, suggest only moderate B-philicity of the GC/GC & CG/CG steps [27, 58]. However, it must be noted that these observed trends were derived by inducing the B to A transition in DNA oligomers via decreasing the relative humidity of the medium by adding ethanol to water-ethanol mixtures (and at a low temperature of 253 K [58]). Therefore, these observed B-philicity trends do not necessarily represent the behaviour of individual dinucleotide steps at physiological conditions and, as such, our calculations are not directly comparable with these experimental results. Many theoretical studies comment that the GC/GC steps are A-philic for example based on MP2/631G* ab intio calculation it was concluded that GC rich sequences favour the A-form over the B-form (59). However, these studies do not include the solvation, salt concentration and configurational entropic effects (via consideration of the valley volumes) incorporated in this work.
B-philic: AC/GT, AA/TT, AT/AT steps
The AC/GT, AA/TT and AT/AT steps show very similar B-philicity characteristics (with a range of ∆ABA of -1.23 to –0.94 kcal/mol). The B-philicity of these steps is in accord with Hunter’s suggestion [59] that AX/XT steps (X=A, C, G or T) prefer the B-form due to steric clashes between the thymine methyl group and the 5’-neighbouring base which block the A-DNA conformations. However, the order of these steps in terms of their relative B-philicity (Table 1) is not in accord with the observed high B-philicity of A‑tract DNA oligomers derived from crystallographic data [24]. However, high B-philicity of the A-tract oligomers is attributed to stabilization of the B-form by the formation of cross-strand hydrogen bonds [60,61]. For shorter DNA segments we expect this effect to be less significant.
A step with bistable characteristics: the GG/CC step
Our calculations suggest that the GG/CC step has only a small preference for B-form over the A-form (∆ABI-A= -0.29 kcal/mol) which is suggestive of a bistable character. Raman spectroscopy studies have shown that that poly(dG).poly(dC) shows structural variability between A and B-form in solution [62]. However, other spectroscopic studies using NMR and circular dichroism have showed that poly(dG).poly(dC) exists only in the A-form in solution [63,64]. This conflict in experimental results is difficult to resolve. However, it is noted that the NMR experiments [64], have been conducted over a range of temperatures, 30-60 ºC. Such rise in temperature could overcome the little free energy barrier (∆ABI-A= -0.29 kcal/mol), switching the GG/CC step into the A-form.
A-philic: TA/TA step
The TA/TA step is the only dinucleotide step which showed a pronounced A-philic character in our computed B-philicity scale (∆ABI-A= +0.73 kcal/mol). This is in good agreement with the results of single crystal X-ray diffraction studies on DNA double helices containing the TATA sequence (e.g. d(GGTATACC)) which were observed to adopt the A-form conformation [65, 66]. Further, the preference for the TA/TA step to adopt the A-form may be of biological relevance given that the TATA sequence is a motif frequently associated with transcription promoter regions [67,68].
Conclusion
he conformational space of DNA dinucleotide steps was described by three collective degrees of freedom derived from a principal component analysis of the Cartesian coordinates of the atoms defining the backbone and sugar torsions (using data from crystal structures in the NDB). The principal conformational subspace spanned by the first three principal components was found to capture ~77% of the total variance while the rest of the projections along higher principal components are essentially unimodal.
The free energy surfaces of all 10 possible dinucletide steps were mapped in the 3D principal component subspace. The topography of an illustrative FES, CA/TG, shows three energy valleys; two of them corresponding to the BI.BI and BII.BII states while the third corresponds to all of the A-family states. The relative energetics of the A-family, BI.BI depend highly on the sequence of the dinucleotide step. Except for the GG/CC, GA/TC and the TA/TA steps, the BI.BI state corresponds to the global energy minimum. The BII.BII state corresponds to a relatively high-energy, yet shallow valley on the FES, suggesting a metastable character. This reflects the suggestion that the observation of the BII conformation in X-ray crystal structures may be a result of crystal packing effects [50,51].
Based on the subspace FES representation, we computed a B-philicty scale, which represents the propensity for a given dinucleotide step to be in the B-form vs. the A-family conformation at near physiological conditions. Variation in the B-philicity of the ten dinucleotide steps was observed. The ten dinucleotide steps were, therefore, grouped into three categories: highly B-philic (GC/GC & CG/CG), B-philic (AC/GT, AA/TT, AT/AT, CA/TG, AG/CT & GG/CC) and A-philic (GA/TC & TA/TA). The computed B-philicity scale agrees well with experimental data on duplex DNA structures in comparable conditions. The high A-philicity of the TA/TA step has important biological significance in view of its structural relevance to the transcriptional TATA promoter regions [67,68].
The free energy surface provides a coherent physical framework for studying the conformational preferences of DNA at a given temperature and environmental conditions. This physical approach to deriving conformational equilibria in DNA may be contrasted with statistical approaches e.g. [55]. A detailed comparison of the results of the two approaches is ongoing. On our physical model further work is currently underway in a number of directions, including the importance of the system representation, both in terms of segment length and better approximations of the free energy surface.
We thank Drs Seishi Shimizu & Chandra Verma for their support and insightful discussions.
- Flatters D, Zakrzewska K, Lavery R (1997) Internal coordinate modeling of DNA: Force field comparisons. J Comput Chem 18: 1043-1055. Link: https://bit.ly/2zt718v
- Sarai A, Jernigan RL, Mazur J (1996) Interdependence of conformational variables in double-helical DNA. Biophys J 71: 1507-1518. Link: https://bit.ly/2M1xLQ2
- Ulyanov NB, Zhurkin VB, Ivanov VI (1982) Analysis of the DNA Conformational Flexibility for the Different Nucleotide-Sequences. Stud Biophys 87: 99-100.
- Zhurkin VB, Poltev VI, Florentev VL (1980) Atom-Atom Potential Functions for Conformational Calculations of Nucleic-Acids. Mol Biol 14: 1116-1130. Link: https://bit.ly/36DvBQ3
- Vologodskii A (2018) Frank-Kamenetskii, DNA melting and energetics of the double helix. Phys Life Rev 25: 1-21.
- Xiao S, Sharpe DJ, Chakraborty D, Wales DJ (2019) Energy Landscapes and Hybridization Pathways for DNA Hexamer Duplexes. J Phys Chem Lett 10: 6771-6779. Link: https://bit.ly/3d7TP7y
- Hunter CA, Lu XJ (1997) DNA base stacking interactions: a comparison of theoretical calculations with oligonucleotide crystal structures. J Mol Biol 265: 603-619. Link: https://bit.ly/3ex5mO5
- Packer MJ, Dauncey MP, Hunter CA (2000) Sequence-dependent DNA structure: Dinucleotide conformational maps. J Mol Biol 295: 71-83. Link: https://bit.ly/3eqnZD1
- ElHassan MA, Calladine CR (1997) Conformational characteristics of DNA: Empirical classifications and a hypothesis for the conformational behaviour of dinucleotide steps. Philos Trans R Soc Lond Ser A-Math Phys Eng Sci 355: 43-100. Link: https://bit.ly/2XCDUaD
- Srivinsan AR, Olson WK (1987) Nucleic acid model building. The multiple backbone solutions associated with a given base morphology. J Biomol Struct Dyn 4: 895-938. Link: https://bit.ly/36zswR2
- Tisne C, Delepierre M, Hartmann B (2010) How NF-[kappa]B can be attracted by its cognate DNA. J Mol Biol 293: 139-150.
- Schroeder SA, Roongta V, Fu JM, Jones CR, Gorenstein DG (1989) Sequence-dependent variations in the 31P NMR spectra and backbone torsional angles of wild-type and mutant Lac operator fragments. Biochemistry 28: 8292-8303.
- Dostal L, Chen CY, Wang AH, Welfle H (2004) Partial B-to-A DNA Transition upon Minor Groove Binding of Protein Sac7d Monitored by Raman Spectroscop. Biochemistry 43: 9600-9609. Link: https://bit.ly/2M7vzqi
- Kim Y, Geiger JH, Hahn S, Sigler PB (1993) Crystal structure of a yeast TBP/TATA-box complex. Nature 365: 512-520. Link: https://go.nature.com/3erKDeu
- Kim JL, Nikolov DB, Burley SK (1993) Co-crystal structure of TBP recognizing the minor groove of a TATA element. Nature 365: 520-527. Link: https://go.nature.com/2M7vP8K
- Becker MM, Wang Z (1989) B-A transitions within a 5 S ribosomal RNA gene are highly sequence-specific. J Biol Chem 264: 4163-4167. Link: https://bit.ly/3c6zHBf
- Mohr SC, Sokolov NV, He CM, Setlow P (1991) Binding of small acid-soluble spore proteins from Bacillus subtilis changes the conformation of DNA from B to A. Proc Natl Acad Sci U. S. A. 88: 77-81. Link: https://bit.ly/3db9VgH
- Flader W, Wellenzohn B, Winger RH, Hallbrucker A, Mayer E, et al. (2001) B-I to B-II substate transitions induce changes in the hydration of B-DNA, potentially mediating signal transduction from the minor to major groove. J Phys Chem B 105: 10379-10387. Link: https://bit.ly/3eqq3Lh
- Pichler A, Rudisser S, Mitterbock M, Huber CG, Winger RH, et al. (1999) Unexpected BII Conformer Substate Population in Unoriented Hydrated Films of the d(CGCGAATTCGCG)2 Dodecamer and of Native B-DNA from Salmon Testes. Biophys J 77: 398-409. Link: https://bit.ly/2Xa2JeU
- Winger RH, Liedl KR, Pichler A, Hallbrucker A, Mayer E (2000) B-DNA's B-II conformer substate population increases with decreasing water activity. 1. A molecular dynamics study of d(CGCGAATTCGCG)(2). J Phys Chem B 104: 11349-11353. Link: https://bit.ly/3eugFGO
- ElSawy KM, Hodgson MK, Caves LSD (2005) The physical determinants of the DNA conformational landscape: an analysis of the potential energy surface of single-strand dinucleotides in the conformational space of duplex DNA. Nucleic Acids Res 33: 5749-5762. Link: https://bit.ly/2XuHNyc
- Urabe H, Kato M, Tominaga Y, Kajiwara K (1990) Counterion Dependence of Water of Hydration in DNA Gel. J Chem Phys 92: 768-774. Link: https://bit.ly/2zAFWA0
- Harmouchi M, Albiser G, Premilat S (1990) Changes of Hydration During Conformational Transitions of DNA. Eur Biophys J 19: 87-92. Link: https://bit.ly/2zAG4iY
- Manning GS (2002) Electrostatic free energy of the DNA double helix in counterion condensation theory. Biophys Chem 101-102: 461-473. Link: https://bit.ly/3epfZSJ
- Nishimura Y, Torigoe C, Tsuboi M (1986) Salt Induced B-A Transition of Poly(dG).Poly(dC) and the Stabilization of a-Form by Its Methylation. Nucleic Acids Res 14: 2737-2748. Link: https://bit.ly/3gu9Kiy
- Wang Y, Thomas GA, Peticolas WL (1989) A Duplex of the Oligonucleotides d(GGGGTTTTT) and d(AAAAACCCCC) Forms an a-Conformational to B-Conformational Junction in Concentrated Salt-Solutions. J Biomol Struct Dyn 6: 1177-1187. Link: https://bit.ly/2zvcfAC
- Ivanov VI, Minchenkova LE (1994) The a-Form of DNA - in Search of Biological Role (a Review). Mol Biol 28: 1258-1271. Link: https://bit.ly/2TKR44l
- ElSawy KM (2016) Energy Landscape of Pentapeptides in a Higher-Order Conformational Subspace. Advances in Physical Chemistry. 2016: 3240674. Link: https://bit.ly/36zu9OE
- Hair JF, Anderson RE, Tatham RL, Black WC (1995) Multivariate data analysis: with readings, 4th ed., Prentice Hall, Englewood Cliffs NJ.
- Krzanowski WJ (2000) Principles of Multivariate Analysis, Oxford University Press.
- Reijmers TH, Wehrens R, Buydens LMC (2001) Circular effects in representations of an RNA nucleotides data set in relation with principal components analysis. Chemom Intell Lab Syst 56: 61-71. Link: https://bit.ly/3c9jN9d
- Berman HM, Olson WK, Beveridge DL, Westbrook J, Gelbin A, et al. (1992) The nucleic acid database. A comprehensive relational database of three-dimensional structures of nucleic acids. Biophys J 63: 751-759. Link: https://bit.ly/3gvvwT2
- ElHassan MA, Calladine CR (1996) Propeller-twisting of base-pairs and the conformational mobility of dinucleotide steps in DNA. J Mol Biol 259: 95-103. Link: https://bit.ly/2X8pct3
- Sutcliffe MJ, Haneef I, Carney D, Blundell TL (1987) Knowledge based modelling of homologous proteins, Part I: Three dimensional frameworks derived from the simultaneous superposition of multiple structures. Protein Eng 1: 377-384. Link: https://bit.ly/2M57e4j
- Kabsch W (1976) A solution for the best rotation to relate two sets of vectors. Acta Crystallogr A32: 922-923. Link: https://bit.ly/2XAJUAT
- Kabsch W (1978) A discussion of the solution for the best rotation to relate two sets of vectors. Acta Crystallogr A34: 827-828. Link: https://bit.ly/2XAJVVt
- Anderberg MR (1973) Cluster Analysis for Applications. Academic Press New York.
- Hartigan JA, Wong MA (1997) A K-means clustering algorithm. Applied Statistics 28: 100-108.
- Mardia KV, Kent JT, Bibby JM (1979) Multivariate Analysis. Academic Press, London 1979.
- Weiner SJ, Kollman PA, Case DA, Singh UC, Ghio C, et al. (1984) A new force-field for molecular mechanical simulation of nucleic-acids and proteins. J Am Chem Soc 106: 765-784. Link: https://bit.ly/2X672bk
- Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, et al. (1996) second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc 118: 2309-2309. Link: https://bit.ly/36CmOOc
- Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, et al. (1983) CHARMM - a Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J Comput Chem 4: 187-217. Link: https://bit.ly/36AhL0K
- Klapper I, Hagstrom R, Fine R, Sharp K, Honig B (1986) Focusing of electric fields in the active site of Cu-Zn superoxide dismutase: effects of ionic strength and amino-acid modification. Proteins 1: 47-59. Link: https://bit.ly/3gwzBXd
- Im W, Beglov D, Roux B (1998) Continuum Solvation Model: computation of electrostatic forces from numerical solutions to the Poisson-Boltzmann equation. Comput Phys Commun 111: 59-75.
- Banavali NK, Roux B (2002) Atomic radii for continuum electrostatics calculations on nucleic acids. J Phys Chem B 106: 11026-11035. Link: https://bit.ly/2ZJfcIs
- Gilson MK, Honig B (1988) Calculation of the Total Electrostatic Energy of a Macromolecular System - Solvation Energies, Binding-Energies, and Conformational-Analysis. Proteins Struct Funct Genet 4: 7-18. Link: https://bit.ly/2ZH9AhO
- Roux B, Simonson T (1999) Implicit solvent models. Biophys Chem 78: 1-20. Link: https://bit.ly/2TMkmQ6
- Caves LSD, Evanseck JD, Karplus M (1998) Locally accessible conformations of proteins: Multiple molecular dynamics simulations of crambin. Protein Sci 7: 649-666.
- Djuranovic D, Hartmann B (2004) DNA Fine Structure and Dynamics in Crystals and in Solution: The impact of BI/BII Backbone Conformations. Biopolymers 73: 356-368. Link: https://bit.ly/2AitLI1
- Dickerson RE, Goodsell DS, Kopka ML, Pjura PE (1987) The Effect of Crystal Packing on Oligonucleotide Double Helix Structure. J Biomol Struct Dyn 5: 557-579. Link: https://bit.ly/3gqKlGB
- Heinemann U, Hahn M (1992) C-C-A-G-G-C-M5c-T-G-G - Helical Fine-Structure, Hydration, and Comparison with C-C-A-G-G-C-C-T-G-G. J Biol Chem 267: 7332-7341. Link: https://bit.ly/3c9kSOj
- Schneider B, Neidle S, Berman HM (1997) Conformations of the sugar-phosphate backbone in helical DNA crystal structures. Biopolymers 42: 113-124. Link: https://bit.ly/3cdHOff
- Shakked Z, Rabinovich D (1986) The effect of the base sequence on the fine structure of the DNA double helix. Prog Biophys Mol Biol 47: 159-195. Link: https://bit.ly/2zF8xnP
- Beckers MLM, Buydens LMC (1998) Multivariate analysis of a data matrix containing A-DNA and B-DNA dinucleotide monophosphate steps: Multidimensional Ramachandran plots for Nucleic acids. J Comput Chem 19: 695-715. Link: https://bit.ly/3gEJ0fo
- Bharanidharan D, Gautham N (2006) Principal component analysis of DNA oligonucleotide structural data. Biochem Biophys Res Commun 340: 1229-1237. Link: https://bit.ly/3es15vi
- Saenger W (1984) Principles of nucleic acid structure. Springer-Verlag New York.
- Wang Y, Thomas GA, Peticolas WL (1987) Sequence dependent conformations of oligomeric DNA's in aqueous solutions and in crystals. J Biomol Struct Dyn 5: 249-274. Link: https://bit.ly/2XG84d0
- Tolstorukov MY, Ivanov VI, Malenkov GG, Jernigan RL, Zhurkin VB (2001) Sequence-Dependent B->A Transition in DNA Evaluated with Dimeric and Trimeric Scales. Biophys J 81: 3409-3421. Link: https://bit.ly/2TKtBAk
- Hunter CA (1993) Sequence-dependent DNA structure. The role of base stacking interactions. J Mol Biol 230: 1025-1054. Link: https://bit.ly/3eotF0r
- Nelson HC, Finch JT, Luisi BF, Klug A (1987) The structure of an oligo(dA).oligo(dT) tract and its biological implications. Nature 330: 221-226. Link: https://bit.ly/2zt9gbW
- Yoon C, Prive GG, Goodsell DS, Dickerson RE (1988) Structure of an alternating-B DNA helix and its relationship to A-tract DNA. Proc Natl Acad Sci U S A 85: 6332-6336. Link: https://bit.ly/2XFkPVp
- Benevides JM, Wang AH, Rich A, Kyogoku Y, van der Marel GA, et al. (1986) spectra of single crystals of r(GCG)d(CGC) and d(CCCCGGGG) as models for A DNA, their structure transitions in aqueous solution, and comparison with double-helical poly(dG). Poly (dC). Biochemistry 25: 41-50. Link: https://bit.ly/3goVoQx
- Mei HY, Barton JK (1988) Tris(tetramethylphenanthroline)ruthenium(II): a chiral probe that cleaves A-DNA conformations. Proc Natl Acad Sci U S A 85: 1339-1343. Link: https://bit.ly/3dd3QjC
- Sarma MH, Gupta G, Sarma RH (1986) 500-MHz 1H NMR study of poly(dG).poly(dC) in solution using one-dimensional nuclear Overhauser effect. Biochemistry 25: 3659-3665. Link: https://bit.ly/2XAbZbj
- Shakked Z, Rabinovich D, Cruse WB, Egert E, Kennard O, et al. (1981) Crystalline A-dna: the X-ray analysis of the fragment d(G-G-T-A-T-A-C-C). Proc R Soc Lond B Biol Sci 213: 479-487. Link: https://bit.ly/36z5c5Y
- Shakked Z, Rabinovich D, Kennard O, Cruse WB, Salisbury SA, et al. (1983) Sequence-dependent conformation of an A-DNA double helix. The crystal structure of the octamer d(G-G-T-A-T-A-C-C). J Mol Biol 166: 183-201. Link: https://bit.ly/2zBVHqx
- Starr DB, Hawley DK (1991) TFIID binds in the minor groove of the TATA box. Cell 67: 1231-1240. Link: https://bit.ly/2yFl8XR
- Patikoglou GA, Kim JL, Sun L, Yang SH, Kodadek T, et al. (1999) TATA element recognition by the TATA box-binding protein has been conserved throughout evolution. Genes Dev 13: 3217-3230. Link: https://bit.ly/36zPxmK

Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

 Save to Mendeley
Save to Mendeley
