The study of the biomechanics of the eye is important for understanding the mechanisms of its functioning and the causes of the development of pathologies. New knowledge helps to better diagnose a number of diseases and develop effective methods of their treatment. The theoretical results obtained can give impetus to new research in this area.
This paper considers a mathematical model of the translational movement of the eyeball as a whole body as a result of the impact of an air pulse on the cornea of the eye (pneumotonometry).
For the pneumotonometry procedure, indicators in the range of 15-22 millimeters of mercury are considered the norm. An increase in indicators above the level of 21 millimeters. This is a sign of the beginning of the formation of glaucoma, and the higher this number, the greater the likelihood that the disease is already present and progressing;
The disadvantage of pneumotonometry is the measurement accuracy. Due to individual anatomical features (corneal thickness and elasticity), readings may differ from the average ("normal") values. In addition, during the examination, the patient may tense the muscles of the eyeball and eyelids, which puts additional external pressure on the eye and leads to an increase in IOP values.
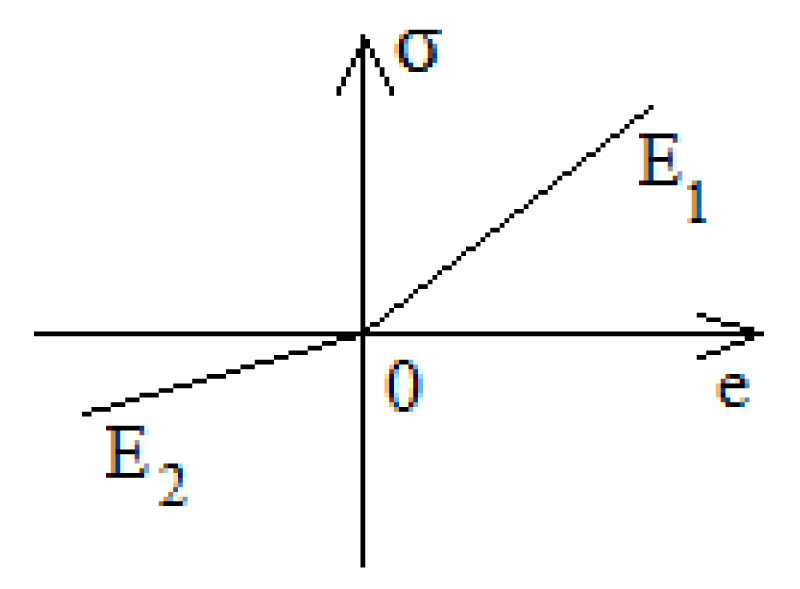
In this case, we consider the effect of an air pulse directed vertically to the cornea. The impulse causes not only the deformation of the cornea but also the displacement of the eyeball as a whole body along the optical axis, as shown by experimental observations [1]. It is noted that this movement begins with some delay in time after the impact of the pulse on the cornea. This is due to the fact that the material of the cornea is two-module - it has different moduli of elasticity for tension and compression in accordance with Figure 1.
Figure 1: Loading scheme for a two-module material.
As a result, the cornea under the action of a pulse of air is deformed in the zone of action (area) of the pulse to the state of applanation with little or no resistance. After passing through the flat state, the cornea (considered as a membrane) begins to work in tension and experiences resistance, so that when a certain amount of stretch is reached, the resistance to further stretching is higher than the resistance to the translational movement of the eyeball as a whole. Along the optical axis.
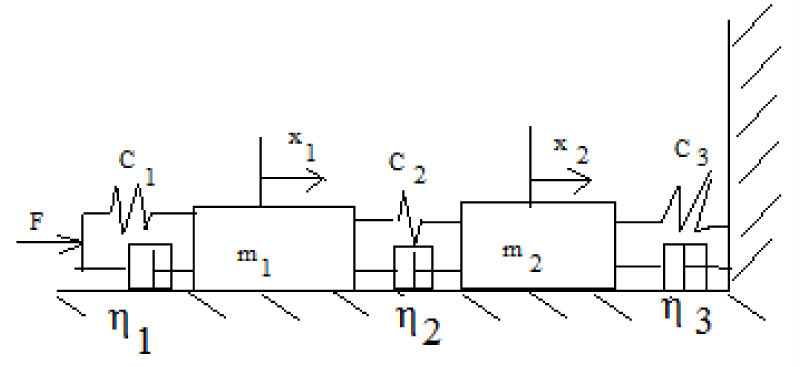
Let us imagine a two-mass model of the eyeball based on the fact that the anterior chamber between the cornea and the lens has a structure and physical and mechanical properties different from the structure and physical and mathematical properties of the vitreous body. Therefore, consider the model of the eye, schematically depicted in Figure 2.
Figure 2: Scheme of representation of the eyeball in the form of a two-mass system.
Part of the eye m2 is located in the orbit and is surrounded by a liquid-like layer that has the property of elasticity and viscosity. Part of the eye m1 has viscoelastic properties.
The boundary between m1 and m2 is formed by the lens and muscle tissues and in the general case also has viscoelastic properties.
The scheme of the eyeball, taking into account the above properties, is shown in Figure 3. Ci - stiffness (elasticity) coefficients, i- viscosity coefficients, m1, m2 - the mass of the anterior and posterior parts of the eyeball.
Figure 3: Structural diagram of the eyeball model for elasticity and viscosity connected in parallel.
The dynamics of the translational movement of the eye model are described by the equations:
In the vector-matrix form, the equations of motion (1) have the form:
Then there are no products x1, x2 in the expressions for the kinetic T and potential energies П.
Therefore, x1 and x2 are the principal (normal). The distinctive function has the form:
The solution of equation (1) is sought in the form:
The characteristic equation has the form:
Denote
We write the solution in the form
If the resistance (viscosity) is large enough, then the aperiodic motion is real.
Experimental studies of biomechanics of the human eye during pneumotonometric tests show that the movement points on the surface of the cornea superposition of several mechanical displacements under the action of an air pulse [2]. Almost simultaneously, the eye as a whole body moves forward along the optical axes and at the same time performs rotational movement around the center of mass of the eye (precession and nutation). Own rotation of the eye around the optical axis is not observed.
Conclusion
In this work, we obtained a mathematical model of the translational movement of the eyeball under the influence of an air pulse.

 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.


 Save to Mendeley
Save to Mendeley
