Journal of Civil Engineering and Environmental Sciences
Structural health monitoring and modal parameters identification of Mezcala Bridge
Miguel Anaya-Diaz1, Francisco J Carrion-Viramontes1, Juan A Quintana-Rodriguez1, Luis A Martinez-Trujano1 and Jose M Machorro-Lopez2*
2Researcher Conacyt, Mexican Institute of Transportation, 12 km State Highway No. 431 “El Colorado-Galindo” San Fandila, 76703, Pedro Escobedo, Querétaro, Mexico
Cite this as
Anaya-Diaz M, Carrion-Viramontes FJ, Quintana-Rodriguez JA, Martinez-Trujano LA, Machorro-Lopez JM (2022) Structural health monitoring and modal parameters identification of Mezcala Bridge. J Civil Eng Environ Sci 8(2): 062-067. DOI: 10.17352/2455-488X.000052Copyright License
© 2022 Anaya-Diaz M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.Since 2016 the Instituto Mexicano del Transporte (Mexican Transport Institute) has continuously instrumented and performed the structural monitoring of the Mezcala Bridge, which is a cable-stayed bridge located in the State of Guerrero, Mexico. In order to identify early damage, several monitoring strategies based on changes in the bridge modal parameters have been implemented. To establish the limits of the parameters, such as the natural frequencies, damping ratios, and mode shapes, it is necessary to characterize the bridge dynamic behavior through monitoring information from the last 3 years, in order to analyze statistically every parameter and simulate different real damage scenarios. Modal parameters are calculated and evaluated every week or after accidents, earthquakes, or strong winds. Applying the proposed methodology based on the Enhanced Frequency Domain Decomposition (EFDD), the modal parameters of the Mezcala Bridge were efficiently estimated and monitored and subsequently, they could be used for finite element model development and calibration in order to evaluate the structural integrity of the bridge.
Introduction
Civil structures are of a great importance in the economic, social, and cultural development of the society. The considerable investment for the construction of buildings and bridges makes that these structures have to be regularly inspected in order to ensure their structural health. Nowadays, periodic visual inspections are carried out to assess the structural conditions of bridges. The typical period for visual inspection assessment is one year and it is limited to the ability and knowledge of the inspectors. On the other hand, visual inspections are incapable to detect internal damages or degradations in the structures, which normally, blossom to the surface when they reach a critical state.
To overcome the visual inspection limitations, in recent years there have been developed modern techniques of analysis based on structural health monitoring (SHM) systems that are capable of identifying and assessing the condition of a structure. The SHM involves the assessment of the structure behavior through time; identifying its parameters that are sensitive to damage and statistical analyses to evaluate its structural condition [1]. The main objectives of SHM applied on bridges are [2]:
- Evaluation of the traveling load.
- Evaluation of the structural performance.
- Evaluation of wind effects and hydrodynamics.
- Assessment of safety.
- Assessment of serviceability.
- Assessment of environmental compatibility.
To achieve those objectives not only necessary the implementation of an SHM system but to development and implementation techniques to analyze the information obtained from the sensors installed in the structure. The structural condition could be evaluated through the changes in the structure’s natural frequencies [3], mode shapes [4], damping ratios [5] and live load response amplitudes [6].
For the above, it is important to identify and characterize the structure’s dynamic behavior through the estimation of its modal parameters. Nevertheless, the signals obtained from the SHM systems are usually embedded in a high noise content; on the other hand, the excitation forces are caused by ambient sources such as vehicles, wind, and seismic motions. Considering the previous, techniques to obtain the structure free-decay functions from ambient vibration data have been developed in order to estimate the modal parameters such as natural frequencies, mode shapes, and damping ratios [7,8]. Nevertheless, the previously mentioned techniques usually present difficulties when dealing with closely spaced modes, such as the ones from a large structure. To overcome these drawbacks, the Enhanced Frequency Domain Decomposition (EFDD) [9] was implemented in this work, which is based on the singular value decomposition of the Power Spectral Density Matrix obtained from the auto and cross-correlation functions of the SHM data. The EFDD technique has been used for health monitoring and modal analysis of different structures including bridges [10-23].
Mezcala Bridge
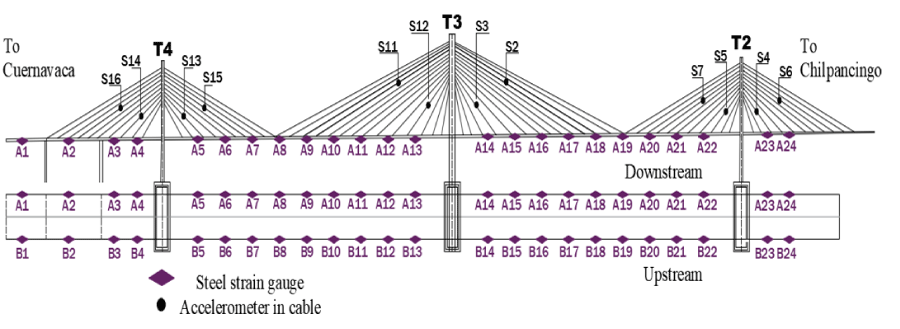
The Mezcala Bridge (Figure 1) is a cable-stayed bridge located in km 221 of the Del Sol Highway in the State of Guerrero, Mexico. The bridge has 911 meters of total length formed by six spans, with a maximum span length of 311 meters. Five of the six spans are supported by cables. The bridge was opened to traffic in 1993. Due to the importance of the Mezcala Bridge in the economic activity of the zone, as well as its construction cost, type of structure, total length, and the seismic zone where it is located, it was selected to be instrumented and monitored in real-time by the Instituto Mexicano del Transporte (IMT).
The instrumentation of the SHM system of the Mezcala Bridge consists on 36 accelerometers, 16 inclinometers, 10 concrete strain gauges, 48 steel strain gauges, and 11 temperature sensors. Each one of these sensors was installed in specific locations in accordance with the structural response of interest, e.g., an accelerometer installed on a stay cable to measure, indirectly, the cable tension force [24].
In the case of the steel strain gauges, they were installed on the bottom flange of the main girders, both Downstream (Sensors A1 to A24) and Upstream (Sensors B1 to B24). The instrumentation of the Mezcala Bridge is shown in Figure 2.
Methodology
In the traditional modal analysis, it is required the measurement ofboth structural response and the excitation force in order to obtain the frequency response functions; from which, the modal parameters are estimated [25]. Nevertheless, for large civil structures is difficult to get controlled excitation sources with enough magnitude to excite the structure, and, added to this, there is the need to close the structure to traffic. An alternative to deal with these drawbacks is the use of natural excitation sources like vehicular traffic, wind, and seismic motions, which are known as ambient vibration testing (AVT). The main advantage of this kind of testing is its relatively low cost and that there is no need to close the structure to traffic.
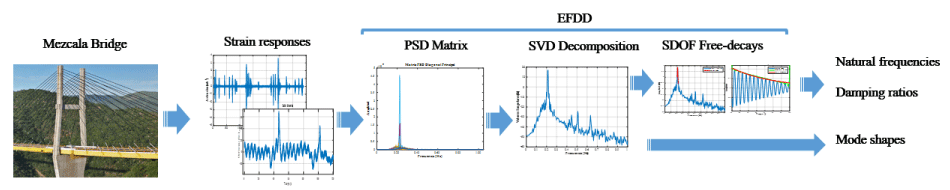
The implemented technique to identify and monitor the modal parameters of the Mezcala Bridge from the recorded ambient vibration signals was the Enhanced Frequency Domain Decomposition (EFDD). In Figure 3 a scheme of the methodology for signal analysis using EFDD is shown.
The first step in the EFDD technique is the estimation of the Power Spectral Density matrix, which is defined in Eq. (1), and it expresses the relationship between the forces and the structural responses
[Ĝxx(iω)]= [H(iω)] [Ĝff(iω)] [H(iω)]T (1)
Where Ĝxx is a matrix of m x m size, being m the number of analyzed channels, whereas Ĝff and H are the force and frequency response matrices, respectively. If the force functions consist of noise and the structure exhibits light damping, the Ĝxx matrix could be decomposed into auto spectral density functions, each one corresponding to a single degree of freedom (SDOF) system as shown in Eq. (2).
[Ĝxx(iω)]= [Ui] [Si] [Ui]T (2)
The matrix Si contains the system singular values and the Ui is a complex matrix containing the system mode shapes. The system resonant frequencies could be pick-peaked by plotting the singular values. Finally, the singular values corresponding to the system SDOF free-decay functions are identified by comparing the mode shape of the resonant values with those from the peak vicinity values through MAC [26], if a singular value has a mode shape correlation of 90% or more with the resonant peak mode shape vector, the singular value is considered a part of the SDOF function.
Once the SDOF singular values are identified, the rest of the singular values are set to zero and the function is converted to the time domain by using Inverse Fast Fourier Transform. The natural frequency and damping factor are estimated from the free-decay function. This process is repeated for all the resonant peaks of the singular value spectrum.
The analysis process of the Mezcala Bridge SHM signals
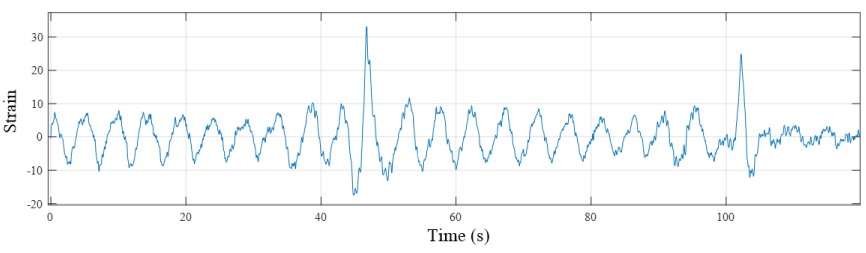
The analyzed signals correspond to strain data obtained from the main girders’ steel strain gauges. The sampling frequency of the SHM systems is 125 Hz. The acquired data is stored in files with a duration of 120 seconds. To reduce the effects caused by the heavy vehicles on the bridge (low frequencies) a Butterworth high-pass filter was applied to the raw data, the cutoff frequency was set to 0.10 Hz. A typical strain signal is shown in Figure 4.
After the signal filtering, the Ĝxx matrix was estimated through the auto and cross-correlations in the frequency domain of the 48 steel strain gauge sensors. For each block of 120 seconds, all the strain data is windowed using a Hanning function and then, they are transformed into the frequency domain by using the Fast Fourier Transform algorithm. In the frequency domain, the data is auto and cross-correlated. Later, the Ĝxx matrix is calculated by averaging several consecutive blocks. The total time of the analyzed continuous monitoring data is one hour (60 blocks).
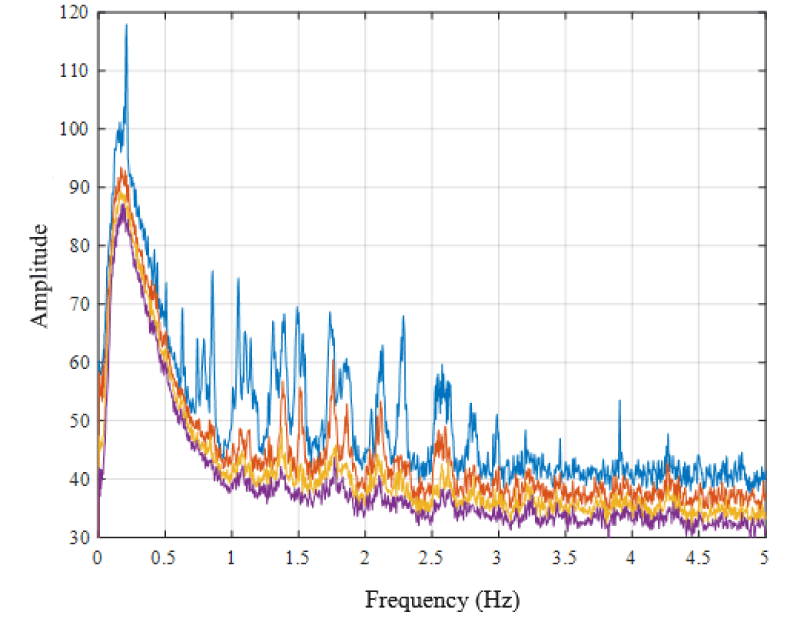
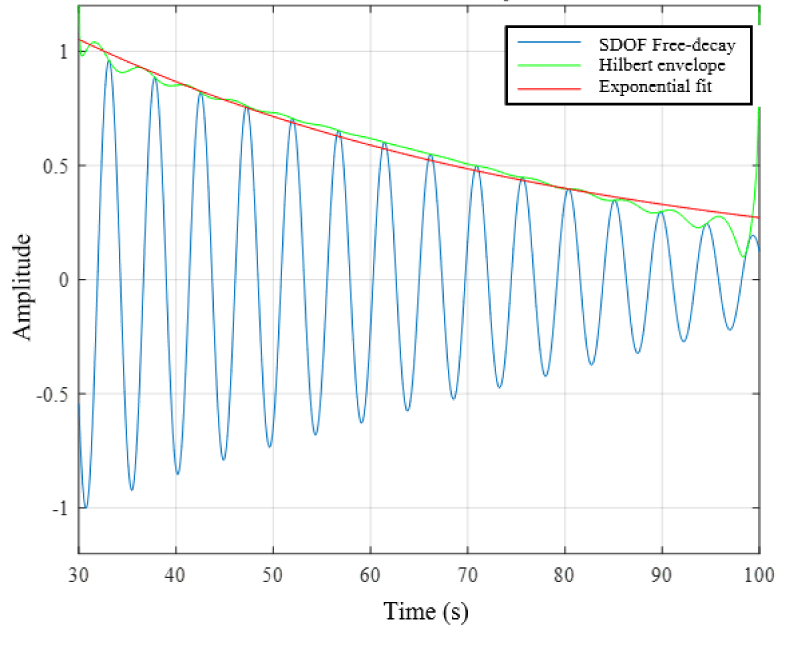
By decomposing the Ĝxx in each frequency by using the Singular Value Decomposition (SVD) technique the singular values and vectors were obtained. In the singular value spectrum obtained (Figure 5), the spectral peaks corresponding to the structural vibration modes are shown. Finally, the SDOF function for each one of the spectral peaks was obtained by identifying their singular values components through MAC. The natural frequency and damping ratio (ζ) were obtained by curve fitting the free-decay function shown in Figure 6.
Results
From the analyzed SHM system strain data with the EFDD technique, 14 modes of vibration of Mezcala Bridge were identified. The modal parameters of each mode are shown in Table 1.
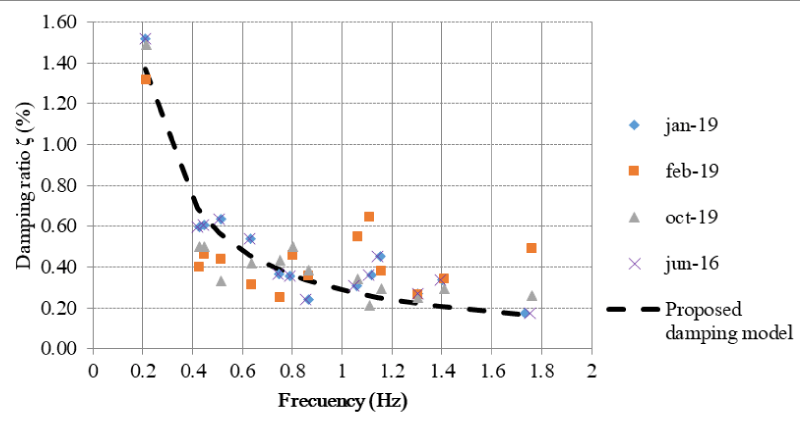
From the estimated natural frequencies and damping ratios, it was found the relationship shown in Figure 7. The monitored data was fitted to the damping equation proposed by Rayleigh [27]; where α is the proportional constant that relates the structure mass with the damping ratio as a function of the natural frequency. The correlation between the proportional damping model with the monitored one was about 92%.
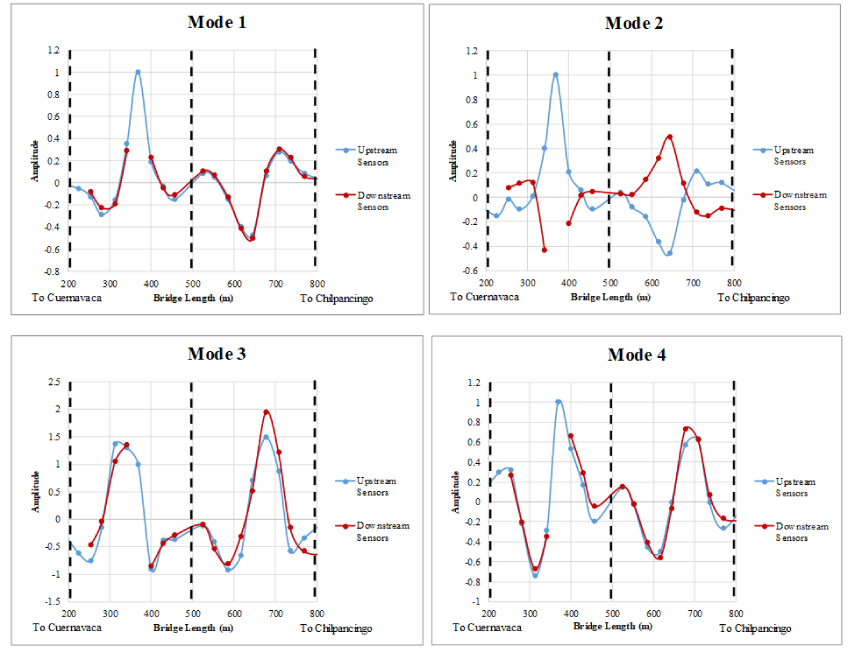
On the other hand, the strain mode shapes of the first four modes of vibration of the Mezcala Bridge are shown in Figure 8. The dashed vertical lines represent the location of the bridge piles.
Conclusion
By analyzing the structural responses of the Mezcala Bridge under ambient vibration conditions with the EFDD technique, it was possible to identify 14 modes of vibration. The natural frequencies of the monitored modes of vibration of the bridge are in a range of 0.20 Hz - 1.80 Hz. From the monitored parameters, it was found a relationship between the natural frequencies and damping ratios, which can be modeled through a mass proportional Rayleigh damping equation. The values of the modal parameters are monitored continuously to identify if there are considerable changes that could be attributable to structural damages or material degradations, especially, after strong seismic events. As part of the continuation of this research, in future works, a tridimensional finite element model of the Mezcala Bridge will be developed and calibrated in order to compare and evaluate the modal parameters obtained, by using the proposed methodology, from a real-life cable-stayed bridge and a numerical model. Moreover, different conditions of damage will be induced in the numerical model and the respective modal parameters will be obtained and compared with the corresponding ones of the healthy bridge, in this way the differences will suggest the presence of damage and the structural integrity of the bridge could be ensured by determining if the current modal parameters are in or out the established limits.
This work was partially supported by the National Council of Science and Technology (Consejo Nacional de Ciencia y Tecnología, CONACYT-Mexico) through the project 34/2018 of the program “Investigadoras e Investigadores por México” del CONACYT (Cátedras CONACYT).
- Farrar C, Worden K. An introduction to structural health monitoring. Philosophical Transactions of the Royal Society A – Journals. 2007; 365: 303-315.
- ISO 18649:2004. Mechanical vibration — Evaluation of measurement results from dynamic tests and investigations on bridges. 2004.
- Salawu O. Detection of structural damage through changes in frequency: a review. Engineering Structures. 1997; 19: 718-723.
- Maia N, Silva J, Almas E, Sampaio R. Damage detection in structures: from mode shape to frequency response function methods. Mechanical Systems and Signal Processing. 2003; 17: 489-498..
- Frizzarin M, Feng M, Franchetti P, Soyoz S, Modena C. Damage detection based on damping analysis of ambient vibration data. Structural Control and Health Monitoring. 2010; 17: 368-385.
- Quintana J, Carrión F, Trujano L, Anaya M, Hernández J, Gasca H, Valenzuela J, Hernández A. Actualización y seguimiento de los índices de desempeño del puente Río Papaloapan. Report: Instituto Mexicano del Transporte, Queretaro, Mexico. 2018; 1-77.
- James G, Carne T, Lauffer J. The natural excitation technique (NExT) for modal parameter extraction from operating wind turbines. Report: Sandia National Laboratory, Albuquerque, New Mexico. 1993; 1–22.
- Juang J. Pappa R. An eigensystem realization algorithm for modal parameter identification and model reduction. Journal of Guidance. 1985; 8: 620-627.
- Brincker R, Ventura C, Andersen P. Damping estimation by frequency domain decomposition. Proceeding of the International Modal Analysis Conference - IMAC XIX, Kissimmee, USA. 2001.
- Saidin S, Kudus S, Jamadin A, Anuar M, Amin N, Ibrahim Z, Zakaria A, Sugiura K. Operational modal analysis and finite element model updating of ultra-high-performance concrete bridge based on ambient vibration test. Case Studies in Construction Materials. 2022; 16: 1-20.
- Altunişik A, Bayraktar A, Sevim B. Operational modal analysis of a scaled bridge model using EFDD and SSI methods. Indian Journal of Engineering and Materials Sciences. 2012; 19: 320–330.
- Hasan M, Ahmad Z, Leong M, Hee L. Enhanced frequency domain decomposition algorithm: A review of a recent development for unbiased damping ratio estimates. Journal of Vibroengineering. 2018; 20: 1919-1936.
- Rodrigues J, Xu M, Santos L. Modal identification from ambient vibration tests on a cable-stayed bridge. Report: LNEC – National Laboratory for Civil Engineering, Structures Department, Lisbon, Portugal. 2004; 1-6.
- Galvin P, Dominguez J. Modal identification of a pedestrian bridge by output-only analysis. Report: Escuela Superior de Ingenieros Universidad de Sevilla, Sevilla, Spain. 2006; 1-6.
- Hamang K. System identification of the Hardanger Bridge using enhanced frequency domain decomposition, Master thesis, Norwegian University of Science and Technology. 2015.
- Andersen P, Brincker R, Peeters B, De Roeck G, Hermans L, Kramer C. Comparison of system identification methods using ambient bridge test data. Proceeding of the International Modal Analysis Conference - IMAC XVII, Kissimmee, USA. 1999.
- Brincker R, Zhang L, Andersen P. Modal Identification from ambient responses using frequency domain decomposition. Proceeding of the International Modal Analysis Conference - IMAC XVIII, San Antonio, USA. 2000.
- Rainieri C, Fabbrocino G. Learning operational modal analysis in four steps. Proceeding of the 6th International Operational Modal Analysis Conference, Gijón, Spain. 1982.
- Magalhães F, Cunha Á, Caetano E, Brincker R. Damping estimation using free decays and ambient vibration tests. Mechanical Systems and Signal Processing. 2010; 24: 1274-1290.
- Rainieri C, Fabbrocino G. Operational modal analysis of civil engineering structures. Springer, New York. 2014.
- Rainieri C, Fabbrocino G, Cosenza E. On damping experimental estimation. Proceeding of the 10th International Conference on Computational Structures Technology, Valencia, Spain. 2010.
- Chen B, Zhang Z, Hua X, Basu B, Nielsen S. Identification of aerodynamic damping in wind turbines using time-frequency analysis. Mechanical Systems and Signal Processing. 2017; 91: 198-214.
- Bendat J, Piersol A. Random data: analysis and measurement procedures. John Wiley and Sons, Hoboken. 2011.
- Carrion F, Lopez J, Quintana J, Guzman A. Nonlinear assessment of cable vibration in a stayed bridge. Experimental Mechanics. 2007; 48: 153-161.
- Marwala T. Finite element model updating using computional intelligence techniques. Applications to Structural Dynamics. Springer, New York. 2010.
- Allemang R, Brown D. A correlation coefficient for modal vector analysis. Proceeding of the International Modal Analysis Conference - IMAC I, Orlando, USA. 1982.
- Cruz C, Miranda E. Evaluation of damping ratios for the seismic analysis of tall buildings. Journal of Structural Engineering-ASCE. 2017; 143: 1-8.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.


 Save to Mendeley
Save to Mendeley
