A possible new conceptual basis in biophysics

For the time being, the biological processes are described based on theoretical apparatus of thermodynamics, mechanics, dynamic systems theory etc. Here a new conceptual basis for description of living objects in their entirety and overall response is suggested. Biology and medicine gain if the organism physiological status could be assessed via prompt and simple measurements. New variables as vitality, biological energy, and synergy are introduced as integral phenomenological characteristics of biological objects. Sinergy is presumed to be a measure of biological selfregulation quality. Biological principle for maximum synergy in undisturbed state is postulated. An equation describing the recovery process of an organism after some disturbance is obtained. The synergy change in possible outcomes after different influences is discussed. The new approach, new variables and laws could form a new science field. This paper could stimulate the scientific thought for further research.

Introduction

The health of human (and generally of biological objects) is estimated via measurement of different vital parameters, indicating the function quality of the different organs and tissues. In addition to these methods, it would be crucial if it were possible to determine some characteristics, reflecting the integral health status of organism. Now there is no such instrumental method. However, the recent development of advanced technologies could promise success in searching of suitable device. This problem is closely related to another fundamental problem–creating of a general theory, describing the integral behavior of a living system after disturbances. It is reasonable to have a phenomenological theory of living matter with a rank of fundamentality like to mechanics, electrodynamics, thermodynamics etc.

Each fundamental science field has its own theoretical basis with respective concepts and laws. So, the basic characteristic in classic dynamics is mass, in electrodynamics–charge and field intensity, in quantum mechanics–wave function, in hydrodynamics–fluxes, in thermodynamics–temperature etc., in chemical kinetics - concentrations of reagents. In biology, there are no own proper quantities.

The most significant attempts to outline the specific of life are based on in being physical theories, and mainly on thermodynamics. Shrödinger considered that the living organisms consume negative entropy (negentropy) [1]. Goodwin created a statistical mechanics and thermodynamics based on kinetics of synchronized biochemical oscillators [2]. Nicolis and Prigogine developed theory of dissipative structures, as an extended irreversible thermodynamics, to explain the self-organization processes in nonequilibrium systems [3]. Mathews, et al., modeled RNA secondary structure applying thermodynamics [4]. Haynie claimed that thermodynamic concepts are of considerable importance for biochemical research [5]. However, all attempts to construct an extended thermodynamics of irreversible processes, including living matter, remain artificial and not adequate, because they not describe the real essence of the living matter. The life systems, as physicochemical systems, subordinate to the Second law of thermodinamics, however not thermodynamic laws are the main laws in the functioning of the life processes. The life systems are self-regulating and adapting systems. Because of that, Blümenfeld noted that the true way to a general life theory is not a biological thermodynamics [6].

An increasing number of authors emphasize the decisive role of information in life phenomena. Quastler represented the problems of the emergence of biological organization in the context of genetic information [7]. Eigen explained the evolution of macromolecular structures taking into account the laws of information exchange [8]. Volkenstein presented the life evolution in its informational aspect [9]. Smith considered that the biological information is inherently a chemical property, but is equally an aspect of control flow and a result of processes equivalent to computation [10]. Interesting quantum biophysical models were proposed, which underline the essential role of neuronal microtubules in information processing in brain [11,12].

The goal here is to describe a biological object in its entirety. However, no cybernetic description is intended. Our idea is to extend the theoretical basis of biophysics via new measurable variables and regularities. Such field of science could be named biodynamics. (Biodynamics as separate field, but not as mixed designation of nonlinear and other models based on the dynamic system theory).

Our view here is restricted to consideration of one fundamental aspect of all living organisms–their behaviour after some influences. In each biological object after deflection of its vital parameters from normal values, self-organization processes run to recover the homeostatic pattern. If a disturbance is incompatible with the life, the organism dies. Otherwise, the organism recovers completely or partially. The process of recovery of the health status is a dynamic process and it could be described by respective mathematical apparatus based on suitable variables. Such an apparatus is proposed bellow. It would be a great benefit if a new quantity could be put in correspondence to the entire organism, a quantity reflecting the health degree of the organism.

Here, such a quantity as well as recovery equation is proposed. For the present, there is no adequate device for measurement of this quantity. Notwithstanding the author is optimist regarding a development of the experimental sciences and technologies.

Basic concepts

To illustrate our idea we can assume for simplicity that a biological object could be assessed in its entirety only by one state variable. We denoted it as vitality (V). (Here a formal analogy could be made with the quantity “themperature” in thermodynamics. With this quantity the state of a given physical object may be described.) The respective metrical unit was named bion (b). We presumed that V is an integral characteristic of the biological object, on macroscopic level. “Vitality” in biology is in some sense similar to “temperature” in thermodynamics. For temperature there is a specific device “thermometer”. The device, which should be constructed to measure vitality, could be called “vitalimeter”. One bion could be defined so that the excellent health standard in human corresponds to vitality of 100 bions. Vitalimeter should be gauge to direct measurement of bions. Vitality could be assumed as a basic concept of a new field, biodynamics.

Here arises the important question: what could be the nature of such quantity. Let us assume that it is possible to establish a dominant tone in human’s (respectively animal’s or plant’s) “aura”. This could be, for instance, the length (frequency) of some electromagnetic emission from the biological object. Electromagnetic waves of different frequencies, generated by human, animal and plant organisms in their metabolic activity and selfregulation were measured yet many years ago [13]. The explorations in this way were continued [14-18]. The advanced technologies today promise success in a searching of a principally new method, which could ensure an integral evaluation of organism’s physiological status via measurement of an appropriate wavelength. As dominant, should be considered that wave, which has maximum brilliance.

In addition, quantity optimal vitality (W) was introduced. W is that value of the vitality, which corresponds to the state of excellent health. Obviously, W depends on the characteristics of homeostasis, evolutionarily established for a given species. The value W was assumed as genetically determined one. During the life, W decreases due to aging processes increasing the organism entropy. However, in time intervals much shorter compared to the lifespan W may be considered as a constant.

Each field of physics operates with specific concept for “energy”. The animate systems are thermodynamic systems (as each material system) but not the thermodynamic laws determine the essence of life. We considered it appropriate to introduce the notion biological energy B. This energy is presumed to be responsible for the maintenance of organism structures and inner selforganization.

In thermodynamics, the balance of internal energy Ei is presented in the form [19,20]:

$d{E}_I=dQ-pd\upsilon -{\displaystyle \sum _r{A}_{r}d{\xi }_r}+{\displaystyle \sum _k{\mu }_{k}d}{n}_k^e\text{ (1)}$

The biological energy B should be a part of the internal energy of a biological object and the energy balance could be present as follows:

$d{E}_I=dQ-pd\upsilon -{\displaystyle \sum _r{A}_{r}d{\xi }_r}+{\displaystyle \sum _k{\mu }_{k}d}{n}_k^e+dB\text{ (2)}$

B ensures the processes of selfregulation (on the basis of enzyme synthesis, resonance energy transfer between biological macromolecules, electric charge transfer, immune cell and antibodies production, DNA repair etc.) and thus is related to the information program encoded in the living system. B is involved in the biological structures and their synchronization. Really, the selfregulation energy is provided by the catabolic reactions of metabolism and ATP hydrolyzes. However, when we would like to deal with the information aspect of life processes, we should consider B as a quantity of biodynamics and present it as a function of new variables. Further, we do not use thermodynamics relations.

The biological energy B was introduced as a function of vitality V (t) and rate of vitality change in time V(t): $B=B(V,\dot{V})$ The function synergy G (V,$\dot{V}$ ) was also introduced as a function uniquely determining the state of a given biological object:

$dG(V,\dot{V})=WdB(V,\dot{V})\text{ (3)}$

Synergy is a measure for the perfect coordination of the enormous number of biophysical and biochemical processes running in the living system. Thus, G reflects the organization degree in the cell/organism (correlation of the regulatory links, structural and functional order). This organization causes the integrity of a biological object. G could be an indicator of the health and youth. G increases (i. e. dG>0) in organism growth and development as well as in recovery and training processes. In aging processes, in severe and chronic diseases G decreases (dG<0). In mature, healthy organism, G may be considered almost constant (dG=0) for relatively long time.

We presumed that vitality V is a measurable quantity. The concept recovery process was defined as a transitory process after some disturbance, in which V(t) tends to reach its optimal value, W (indicating the normal health status), i. e. V(t)→W. In disturbed state V(t) should be less than W.

Regarding recovery processes, one can write the following equation for the balance of biological energy B:

dB=dU+dZ–dR (4)

where the energy U is related to the information potential maintaining the homeostasis. It consists of standard genome energy U_W=const, characteristic for a given species, and potential recovery energy U_V:

$U=U_w+U_v\text{ (5)}$

U_W works in normal, undisturbed state of organism. U_V switches at disturbances. U_V should be proportional to the difference W–V(t), i. e. U_V=K (W–V). U_V should be a positive function and the simplest expression is a positive determined quadratic form:

$U_V=\frac{1}{2}K{(W-V)}^2\text{ (6)}$

Here K ([K]=[kg m b^–2 s^–2]) is homeostatic inductivity, representing the strength of the feedback control. U has its minimum at V(t) = W, when U = U_W. A significant difference W–V(t) needs a significant recovery energy. In a sick man, U_V could be enhanced via good diet and invigorating drugs. The normalized cell metabolism ensures higher ATP levels, which improves the interaction of regulatory links. Thus, U_V increases.

Quantity “power of immune response” P could be introduced on phenomenological level. It should be proportional to the rate of change of the vitality, i. e. $P=M\dot{V}$ . To be a positive function P should be constructed as follows:

$P=M{\dot{V}}^2\text{ (7)}$

where M ([M]=[kg m² b^–2 s^–1]) is immune memory coefficient. The immune reaction has a cumulative effect. At a given moment, the state of the organism depends on the summary effect of immune response in all prior moments. Therefore, the immune response energy Z in the recovery process could be given in the form:

$Z(t)={\displaystyle \underset{t_0}{\overset{t}{\int }}P(\tau )d\tau =}{\displaystyle \underset{t_0}{\overset{t}{\int }}M}\dot{V}{(\tau )}^{2}d\tau \text{ (8)}$

Here we do not differentiate cell and humoral immunity because the organism behavior is considered on phenomenological level and we are interested in the total effect of immune response.

The accomplishment of the recovery process may be embarrassed due to waste products of metabolism (non-fully oxidized substances, macromolecules damaged by free radicals) and toxicants (heavy metals, bacterial and virus toxins etc.) occurring in cell and decreasing the efficiency of metabolic processes and hence of selfregulation. Therefore, the total biological energy B could decrease at expense of energy of metabolic resistance R. It is reasonable to suppose that R is proportional to the rate of change of the vitality .$\dot{V}$ Thus, R could be defined in the form:

$R=\frac{\text{1}}{\text{2}}A{\dot{V}}^{\text{2}}\text{ (9)}$

where A ([A]=[kg m² b^–2]) is metabolic resistance coefficient.

The coefficients K and M decrease but A increases with the aging progress. However, they could be assumed constant in periods much shorter than the lifespan.

Taking into account (3), (4), and (5), one can present the time derivative of G in the form:

$\dot{G}=W\dot{B}=W({\dot{U}}_V+\dot{Z}-\dot{R})\text{ (10)}$

Hence having in mind (6), (8), and (9), the rate of the synergy change in time during a recovery process can be obtained as,

$\dot{G}=W[-K(W-V)+M\dot{V}-A\ddot{V}]\dot{V}=W\Phi \dot{V}\text{ (11)}$

where

$\Phi =[-K(W-V)+M\dot{V}-A\ddot{V}]\text{ (12)}$

could be determined as biological recovery force. It consists of

${\Phi }_U=-K(W-V)\text{ (13)}$

biological force of homeostatically orchestrated feedback control;

${\Phi }_Z=M\dot{V}\text{ (14)}$

biological force of immune response;

${\Phi }_R=A\ddot{V}\text{ (15)}$

biological force of the metabolic resistance.

Based on (13), (14), and (15), the expression (12) could be presented in the form:

$\Phi ={\Phi }_U+{\Phi }_Z-{\Phi }_R\text{ (16)}$

The dimension of $\Phi$ is: [${\Phi }_U$ ]=[${\Phi }_Z$ ]=[${\Phi }_R$ ]=[$\Phi$ ]=[kg m² b^–1 s^–2].

From (16) it is seen that a condition for complete recovery is: ${\Phi }_U+{\Phi }_Z>{\Phi }_R$ .

We postulated the following principle for the biological systems:

$G(W)=\max G(V,\dot{V})\text{ (17)}$

This principle is specific for life. It means that the synergy of a biological object in its normal, undisturbed state has maximum. The diminished G after an unfavorable influence, begin to increase in the recovery process, i.e. dG>0, reaching its maximum value. G(W) corresponds to healthy organism.

Recovery process

Here such recovery processes are presumed that run within a time interval much shorter than the organism lifespan. We tried to obtain differential equation, describing a recovery process. Possible disturbances could be acute infectious diseases, severe environmental influences, intoxications, traumata etc. After such a transitory disturbance the vitality V of the living object temporarily deflects from the optimal vitality W. Due to homeostasis information potential the feedback control switches and immune reaction starts to restore the normal physiological state.

One of the most profound concepts in theoretical physics is that the equations of motion in different fields can be obtained based on integral variational principles. The variational principle of Hamilton is an integral principle. The Hamilton principle allows a common treatment of dynamic problems in mechanics, electrodynamics, optics, thermodynamics, quantum mechanics etc. The basic equations in physics can be derived by means of appropriately chosen Lagrangeans. This approach has a great heuristic concern. The presence of variational principles in almost all fields of physics shows that there is a basic law of the nature. A variational principle of Hamilton type could be essential in fields, where there are yet no other approaches.

For our purpose we chose the Lagrangean $L=L(V(t),\dot{V}(t),t)=U(V)+Z(t)-R(\dot{V})$ . The variational principle could be presented in the form:

$\Gamma ={\displaystyle \underset{t_0}{\overset{T}{\int }}(U+Z-R)dt}=\max \text{ (18)}$

where U, Z and R are determined by the equations (5), (6), (8) and (9).

After variation of (18)

${\Gamma }^{\prime }(\epsilon )|{}_{\epsilon =0}=0$

where ε is an arbitrary parameter, the following ordinary differential equation was obtained:

$\ddot{V}+\frac{2M}{A-2M(T-t)}\dot{V}+\frac{K}{A-2M(T-t)}V=\frac{KW}{A-2M(T-t)}\text{ (19)}$

under initial conditions:

$V(t_0)=V_0\text{ and }\dot{V}(t_0)={\dot{V}}_0\text{ (20)}$

This equation could be considered as a basic equation of biodynamics regarding processes of health recovery after acute diseases or passing disturbances.

Here $V_0$ is the state of the disturbed biological object from which the recovery process starts and ${\dot{V}}_0$ is the start rate of time change of V. T is the continuance of the recovery process. Equation (19) has physical sense and aperiodic solution under the conditions:

$A>2MT\text{ (21)}$

$M^2>K(A-2MT)\text{ (22)}$

If (22) is not valid and $K>\frac{M^2}{A-2MT}$ , an “over”-regulation takes place and an over-shoot time course of the recovery process appears. Such one is observed most often in younger organisms as well as in allergic reactions.

The conditions (21) and (22) essentially restrict the range of the possible parameters’ values. This indicates a very important characteristic of equation (19). Reasonable solutions could be obtained only in case of strongly determined relations between the coefficients. In fact, this situation is consistent with the principles of the biological homeostasis.

To determine the real value of W for different species and different ages, many targeted investigations should be carried out and many empirical data should be collected. In addition, empirical data help to establish the most probable period T for different diseases. When all parameters are known the state of the biological object might be calculated at each moment, and the recovery course would be predicted.

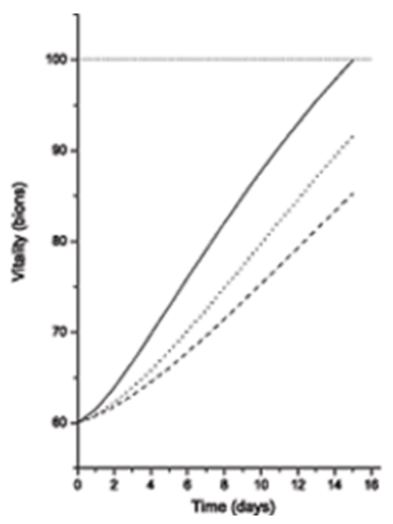
In Figure 1 three numerical solutions of equation (19) are presented. They correspond to three possible time courses of recovery processes. A time interval of T=15 days for the recovery period was arbitrary chosen. A value of 100 bions for optimal vitality W was assumed. The initial conditions were V₀=60 bions and $\dot{V}$ =0.6 bions/day. The displayed time courses were calculated at different values of the characteristic parameters. The dash line corresponds to worsened immunity status; therefore, the organism does not reach a complete recovery. The dot line corresponds to worsened metabolic medium (free radicals, toxins etc.); once again the organism does not reach the level W= 100 bions.

Figure 1: Time courses of the vitality V during the recovery process after some disturbance. Solid line: A=10, M=0.3, K=0.069; dash line: A=10, M=0.2, K=0.04; dot line: A=13, M=0.3, K=0.069.

Possible outcomes after influences

It seems, the possible influences, which a living organism undergo, could be systematized in three main classes: disturbances, severe conditions, and training. Here “disturbances” are understood as fleeting impacts; “severe conditions” are assumed as unfavorable long lasting environmental or life mode circumstances; “training” is considered as purposive, systematic actions to extent the physiological capabilities of organism.

Below are presented the possible outcomes for the biological object after the different influences:

Disturbance → Recovery

→ Chronic disease

→ Death

Severe conditions →Chronic disease

→Death

→Adaptation

Training → Enhancement of the physiological status

The essence of the outcomes and the evolution of V, W, and G are presented below:

Recovery–Restoration to original state V→W, dG>0

Adaptation–Going in new stable state W→W*, W*>=< W, dG≥0

Training–Going in new, improved state W→W*, W*>W, dG>0

Chronic disease–Going in new, worsened state V→ V_chronic <W, dG≤0

Destruction–Going in process before death dV<0, dp>G<0

Death–Going in terminal state V=0, G=0

In recovery process, the deflected vitality V tends to restore its optimal value W. This process is accompanied with synergy increase. Adaptation performs mainly in the following ways: phenotypic accommodation resulting partly in synthesis of adaptive enzymes; and genotypic readjustment. In some sense, adaptation provides a new equilibrium between the organism and medium. The rightly conducted training leads to enhancement of the organism functional level. Then the optimal vitality W* in the new state should be higher compared to W before the training process. Thus, in several individuals (at systematic training) W* may become higher for a relatively long time compared to the statistically mean W for that species. In chronic problems V can not reach W and respectively G declines in some extent to a value of G_chronic, which remains less than the maximal synergy G(W) at normal status. At death, naturally both vitality and synergy vanish.

Sinergy and entropy evolutions during the lifespan

Here the evolutions of synergy G and entropy S in the lifespan scale are commented. The optimal vitality W decreases in lifespan scale due to aging processes. The following cases could be distinguished in synergy G and entropy S correlations during the lifespan (synergy is a quantity, specific only for the living systems):

1) During development and growth:

dG>0 dS>0 dG>dS

2) Near completion of development and growth:

G=max dS>0

3) In mature age:

dG£0 dS0 dG<dS

4) In aging:

dG<0 dS>0 dG£dS

5) At death:

G=0 S=max

In all periods of life, S increases (dS>0 is equivalent to S↑) according to the second law of thermodynamics. 1) In the period up to the age about 25 years the selforganization and selfregulation tend to their complete perfection, and this process quantitatively could be expressed with the increase of synergy G, i. e. dG>0 or G↑. In this period, G increases more intensively than S. This means that in spite of entropy generation, the functional integrity of the organism remains in its best form. 2) About 25–30 years G has its maximum. 3) The mature age covers different age periods in different individuals, depending on the environmental conditions and life mode. Most broadly, it ranges in the interval 25–50 years. In this period, G remains almost constant but at the end of the period begins to decrease. However, G decreases slowly than S increases. This means that in spite of “the wearing out” of the organism, its selfregulation is still reliable, and its potential for rehabilitation and keeping fit is good. 4) After the age of 50–60 years, G steadily decreases and its decrease rate is commensurable with the increase rate of S. This means that together with the reduction of tissue elasticity and functional capacity, the organism loses also the capability of prompt and qualitative response to unfavorable conditions. 5) At death, S reaches its maximum and G does not already exist.

Conclusion

Several biological processes are well described using the theoretical basis of different fields of physics. The overall behavior of a biological object could be studied in cybernetics aspect. Here another approach was first proposed. A quantity “vitality” V, presumed as measurable one, was put in correspondence to overall physiological status of organism. Vitality uniquely characterizes a biological object in phenomenological context (similarly as the quantity “temperature” in thermodynamics). As functions of V, “biological energy” B and “synergy” G were defined. A principle of maximum synergy in undisturbed state of organisms was postulated. An equation was obtained, which solution represents the vitality time course of a given disturbed biological object in its recovery process. Thus, the physiological behavior of an organism would be explored and predicted. The solutions of the equation could be reasonable only in case of a precise correlation of the parameters K, M, and A. This situation corresponds to the nature of homeostasis. Thus, a theoretical basis was outlined, which appears an extension of the theoretical basis of biophysics. It is adequate to specify such a field as biodynamics.

The possible outcomes after influences were commented. In recovery process and adaptation, the synergy G of a biosystem increases. In training process, the optimal vitality W rises. In chronic problems the synergy is less than G(W) at the normal status. The changes of the synergy and entropy at the different stages of the organism’s life were assessed. Entropy S increases in all periods of the life because of the second law of thermodynamics, valid for all mater. In the period of development and growth, the synergy G increases more intensively than S. Therefore, not only energy devaluation runs in organisms, but also a raise of the energy worth (expressed by synergy increase) takes place! In the mature organism, G remains almost constant and then decreases, however, slowly than S increases. In senescence, G and S change with almost equal rates (S increases and G decreases).

Biodynamics approach could be important not only in theoretical and philosophical context but also for practical purposes as a new step in exploration of the organism’s overall response to several disturbances, diseases, and environmental impacts. The work is heuristic at this stage because the device “vitalimeter” is yet not constructed. However, if such a device were created, this would revolutionize biology and medicine. Thus, a further development of the idea proposed here seems to be quite realistic.

1. Shrödinger E (1944) What Is Life? University Press, Cambridge. Link: http://bit.ly/36NmhYH
2. Goodwin BC (1963) Temporal Organization in Cells, Academic Press Inc Ltd London. 27: 497-500. Link: http://bit.ly/35EoZiT
3. Nicolis G, Prigogine I (1978) Self-organization in Nonequilibrium Systems. From Dissipative Structures to Order through Fluctuations. John Wiley and Sons, New York London Sydney Toronto. Link: http://bit.ly/2kpToiI
4. Mathews DH, Diamond JM, Turner DH (2001) The application of thermodynamics to the modelling of RNA secondary structure, In: Di Cera E (ed.) Thermodynamics in Biology, Oxford University Press, Oxford New York 177-202.
5. Haynie DT (2001) Biological Thermodynamics. Cambridge University Press, Cambridge. Link: http://bit.ly/35CmduP  
6. Bljumenfeld LA (1974) Problems of Biological Physics, Naouka Publishing House, Moscow (In Russian).
7. Quastler H (1964) The Emergence of Biological Organization. Yale University Press, New Haven and London 83. Link: http://bit.ly/2k1hJLE
8. Eigen M (1971) Molekulare Selbstorganistion and Evolution (Self organization of matter and the evolution of biological macro molecules). Naturwisswnschaften 58: 465-523. Link: http://bit.ly/2S6XOJK
9. Volkenstein MV (1994) Physical Approaches to Biological Evolution, Springer Verlag, Berlin Heidelberg. Link: http://bit.ly/2jZID6D
10. Smith E (2008) Thermodynamics of natural selection I: Energy flow and the limits on organization. J Theor Biol 252: 185-197. Link: http://bit.ly/2MbjJvu
11. Hameroff S, Penrose R (1996) Orchestrated reduction of quantum coherence in brain microtubules: A Model for consciousness. Math Comput Simul 40: 453-480.  Link: http://bit.ly/2tqvJCP
12. Craddock TJA. Tuszynski JA (2009) A Critical Assessment of the Information Processing Capabilities of Neuronal Microtubules Using Coherent Excitations. J Biol Phys 36: 53-70.  Link: http://bit.ly/34vjpy8
13. Presman AS (1968) Electromagnetic fields and living nature. Naouka Publishing House, Moscow.
14. Cadenas E (1984) Biological Chemiluminescence. Photochem Photobiol 40: 823-830. Link: http://bit.ly/2S8WBBQ
15. Elizarov AA (1997) Instrumental methods for investigating physical fields of biological objects. Measurement Techniques 40: 700-707. Link: http://bit.ly/2M955Fh
16. Sauermann G, Mei WP, Hoppe U, Stab F (1999) Ultraweak photon emission of human skin in vivo: influence of topically applied antioxidants on human skin. Methods Enzymol 300: 419-428.  Link: http://bit.ly/2S9EtHQ
17. Kobayashi M (2003) Spontaneous ultraweak photon emission of living organisms-biophotons-phenomena and detection techniques for extracting biological information. Trends Photochem Photobiol 10: 111-135. Link: http://bit.ly/2tyFuPA
18. Kobayashi M, Kikuchi D, Okamura H (2009) Imaging of Ultraweak Spontaneous Photon Emission from Human Body Displaying Diurnal Rhythm. PloS One 4: e6256. Link: http://bit.ly/2MbkW67
19. Prigogine I, Defay R (1954) Chemical thermodynamics. Longmans Green and Co, London New York Toronto. Link: http://bit.ly/2PFeWF3
20. Haase R (1963) Thermodynamik der Irreversiblen Prozesse. Dr. Dietrich Steinkopff Verlag, Darmstadt. Link: http://bit.ly/2MckOmK