Statistical analysis of regional variation and factors associated with birth weight of babies in Ethiopia: Multilevel ordinal logistic regression

Background: The weight of a newborn is measured for the first time shortly after birth. The World Health Organization divides newborns’ birth weight into three categories: low birth weight (2.5 kg), normal birth weight (2.5 kg-4 kg), and high birth weight (> 4 kg). Both the mother and the infant are at risk of mortality and morbidity as a result of their birth weight. Using hierarchical data, there is scant evidence in Ethiopia of factors linked with birth weight. The goal of this study was to use a multilevel ordinal logistic regression model to investigate geographical variance and factors related to baby birth weight.

Methods: Using missing factors in datasets, data for this study was collected from the Ethiopia Demographic Health Survey 2016. To address missing data and increase the inference’s reliability, hot deck multiple imputations were utilized. A multilevel ordinal logistic regression model was used to examine factors associated with birth weight. R software was used for analysis.

Results: The study took into account a total of 8,328 newborns. According to a descriptive study, 1292 (15.5%) of the 8,328 babies were born with low birth weight, 6143 (73.8%) were born with normal birth weight, and 893 (10.7%) were born with high birth weight. Mother’s age, residence, mother’s age at first birth, wealth index, BMI, anemia level, gestational age, total children, mother delivery, multiple pregnancies, and baby’s sex were all found to be significant factors associated with a birth weight of Ethiopian babies in a multilevel ordinal logistic regression analysis.

Conclusions: The multilevel ordinal logistic regression analysis revealed that there was significant variance in baby birth weight between and within Ethiopian regions. Among the three multilevel models, the random coefficient model fits the data the best.

Introduction

The weight of a newborn is measured for the first time shortly after birth. It should be measured within the first hour of life for live births before considerable post-natal weight loss occurs. Birth weight is frequently used as a measure of a society’s health status. Birth weight has been demonstrated to be a major determinant of a newborn’s chances of survival. WHO categorized babies’ birth weights as Low Birth Weight (LBW) (less than 2.5 kg), Normal Birth Weight (NBW )(2.5-4 kg), and High Birth Weight (HBW) (more than 4 kg) based on their birth weight, independent of gestational age (WHO, 1993). As a result, LBW is divided into two categories: very low birth weight (less than 1.5 kg) and extremely low birth weight (less than 1.5 kg) (less than 1 kg). Similarly, HBW can be subdivided into Class I macrosomic (4-4.499 kg), Class II macrosomic (4.5-4.999 kg), and Class III macrosomic (≥5 Kg) ) [1].

According to a WHO report from 2019, one in every seven live births (20.5 million) babies worldwide suffered from low birth weight, with the majority of cases occurring in low- and middle-income countries and 95.6 percent in developing countries, whereas the frequency of HBW in the world is increasing due to an increase in diabetic and BMI cases. The prevalence of HBW, on the other hand, was determined to be between 1.6 percent and 28 percent of all births, with a frequency that fluctuates depending on the results from different nations [2]. Similarly, the prevalence of HBW was higher in developed countries and among women of high socioeconomic standing, ranging from 5 to 20% of the population [3].

Globally, the prevalence of LBW has slightly declined; however, the rate in many developing countries is still quite high. In 2019, WHO estimated that the prevalence of LBW in North America was 7.9%, South Asia was 27%, Western Europe was 6.9%, and the Middle East and Northern America was 11.3%. On the other hand, the prevalence of HBW was highly ranging from 5 to 20% of all births [4]. In the USA, the HBW rate was 8.0% [5], in Europe and other developed countries reported that the prevalence of HBW was between 5% and 20% [6].

The global prevalence of LBW has decreased marginally, but the rate in many underdeveloped nations remains high. According to WHO, the prevalence of LBW was 7.9% in North America, 27 percent in South Asia, 6.9% in Western Europe, and 11.3 percent in the Middle East and Northern America in 2019. The prevalence of HBW, on the other hand, was considerable, ranging from 5 to 20% of all newborns [4]. The HBW rate in the United States was 8.0 percent [5], whereas the prevalence of HBW in Europe and other industrialized countries were reported to be between 5 and 20%[6].

A study of low- and middle-income nations in Africa, Asia, and Latin America found that HBW prevalence ranged from 0.6 percent in India to 15.2 percent in Algeria [3]. According to a cross-sectional survey conducted in Iran, HBW accounts for 9% of the population (Jasim, et al. 2018). According to a study conducted in South China in 2017, the proportion of LBW was 8.1 percent and the amount of HBW was 4 percent [7].

In addition, the study found that in the Democratic Republic of Congo, Angola, Kenya, Niger, and Uganda, the prevalence of HBW was 2.7 percent, 3.1 percent, 3.9 percent, 8 percent, and 9.1 percent, respectively [3]. In Ethiopia, the prevalence of LBW was 11% among babies weighing less than 5% of their birth weight in 2011. In the 2016 EDHS, however, just 14 percent of births had information on birth weight. 13 percent of these babies were born weighing less than 2.5 kilograms. The prevalence of HBW, on the other hand, was not documented in all EDHS reports.

LBW is a proxy measure of intrauterine malnutrition and gestational age, and it is a risk factor for babies, leading to mortality and morbidity, as well as the development of diseases that manifest later in life, such as type 2 diabetes, hypertension, epilepsy, underweight, birth injury, deafness, and cardiovascular diseases [1,8-10]. LBW has also been linked to growth and neurocognitive development problems [11]. HBW, on the other hand, has been linked to obstetric complications in both mothers and babies, including death, delayed labor, increased need for cesarean delivery, postpartum hemorrhage, fresh stillbirth, being overweight, having an Apgar score of less than 7 per 5 minutes, birth injuries, and cancer development [12-14].

In Ethiopia, the prevalence of birth weight has geographical variation. The study conducted in Hosanna Town showed that the proportion of LBW was 11% [11], in Dessie town was 15.6% [15], in North Shewa zone (Oromia) was 12% [16], in Bale zone was 33.33% [17], in Hawassa was 11.86% [18] and in Mekelle city was 19.1% [19]. On the other hand, the study conducted in Mekelle city revealed that the proportion of HBW was 19.1% [20], in Hawassa was 11.86% [21] and in Debre Markos was 33.33% [22]. Further, a cross-sectional study in the Tigray region found that 10.5% and 6.68% incidence of low birth weight and HBW respectively [19].

Multilevel models (also called hierarchical linear models, nested data models, and mixed models) are statistical models that have multiple levels of variation. Multilevel modeling is used to describe hierarchically structured data in which units at one level are nested with units at a higher level. The use of a multilevel model allows researchers to investigate the effects of group and individual level variation on observations within and between groups at the same time [23]. The EDHS, 2016 data set was used in this analysis, and it was based on two-stage stratified cluster sampling with correlated individual observations. The lower-level units in this study are babies who are nested within higher-level units (regions). Using a hierarchical dataset, there is limited information in Ethiopia on factors linked with birth weight. It was because of this that the researcher decided to perform a study on baby birth weight. As a result, the factors related to baby birth weight were investigated in this study by using regional variation as a random effect in the multilevel analysis.

Methods

Source of data

The Ethiopia Demographic and Health Survey (EDHS) performed by the Central Statistics Agency (CSA) in 2016 provided the data for this study. It is a nationwide large-scale dataset of demographic and health surveys done by the Central Statistical Agency (CSA) with a nationally representative sample from 9 regions and two administrative cities from January 18, 2016, to June 27, 2016. For this study, the baby’s birth weight data was taken from the 2016 EDHS. The survey used a multistage cluster sample based on the 1994 Population and Housing Census sample frame to acquire and provide information on the following domains’ basic indicators of health and demographic variables of interest: Ethiopia as a whole, urban and rural areas (each with its own domain), and all geographical areas (nine regions namely: Tigray, Afar, Amhara, Oromia, Somali, Beneshangul-Gumuz, SNNP, Gambela, and Harari regional states and two city administrations: Addis Ababa and Dire Dawa).

This multistage 2016 EDHS dataset is organized hierarchically. This study’s hierarchy is as follows: newborns are level one and regions are level two. This suggests that newborns are clustered in areas. In EDHS data, missing values are widespread. A few variables in this study had missing values. Thus, after accounting for the missing information, the study’s analysis was given on 8,328 newborns out of 41,392 all-born babies in Ethiopia throughout the study period.

Study population

The study population for this study was all live babies in the five years who were residents of the nine regions and two administrative cities of Ethiopia during the survey period.

Inclusion and exclusion criteria

All weighted babies and missing values of birth weight of babies in EDHS 2016 in sampled areas were included in the study. All babies who have not been weighted at birth were excluded.

Variables in the study

The dependent variable of the study is the birth weight of the baby. The categories of outcome are LBW, normal birth weight, and HBW which is an ordinal response variable, Whereas, the independent variables which are the most factors associated with a birth weight according to different literature are; mother age, region, residence, maternal age at 1^st birth, religion, marital status, mother educational level, wealth index, body mass index, Gestational age, anemia level, smoking cigarette, antenatal visit, total children mother’s delivery, multiple pregnancies, baby’s birth order, and sex of the baby.

Missing data and handling missing data

Missing data occur in survey research because an element in the target population is not included in the survey’s sampling frame (non-coverage), because a sampled element does not participate in the survey (total non-response) and because a responding sampled element fails to provide acceptable responses to one or more of the survey items (item nonresponse). Missing data commonly occur in demographic and health surveys and are defined as no data values being stored for a variable or variables.

Several methods and strategies are available to handle missing data. From them, list-wise deletion (delete cases), imputation, KNN-imputation, regression, and others. Handling missing data has three advantages. First, the method yield unbiased estimates of a variety of different parameters. Second, the methods include a way to assess the uncertainty about the parameter estimates, and third, the method should have good statistical power. Therefore, the researcher used the hot-deck imputation method which involves replacing missing values of one or more variables for a non-respondent (called the recipient) with observed values from a respondent (the donor) that is similar to the non-respondent with respect to characteristics observed by both cases.

Methods of data analysis

The ordinal logistic regression model: Ordinal logistic regression is a type of logistic regression analysis when the response variable has more than two categories with having natural order or rank. In statistics, the ordered logit model (also ordered logistic regression or proportional odds model), is a regression model for the ordinal dependent variable.

Multilevel logistic regression model: The multilevel logistic regression model is appropriate for research signs where data for respondents are organized at more than one level (i.e., nested data). The units of analysis are usually individuals at a lower level (babies) who are nested within contextual/aggregate units at a higher level (regions).

The advantage of using multilevel ordinal analysis is the possibility to estimate the relationship between log odds of more than two ordinal categorical response variables on different levels with a set of independent variables. Therefore, in this study, multilevel ordinal logistic regression analysis of the data was used to identify the factors associated with the birth weight of babies and checked the variation of birth weight of babies within and across the regions in Ethiopia.

Two-level ordinal logistic regression model: Multilevel analysis is a methodology for the analysis of data with complex patterns of variability, with a focus on nested sources of variability. The best way to analyze multilevel data is an approach that represents within-group as well as between-group relations within a single analysis, where ‘group ‘refers to the units at the higher levels of the nesting hierarchy. For instance, a study of ‘babies’ within regions means that not only unexplained variation between babies‘, but also unexplained variation between ‘regions ‘is considered a random variable. This can be expressed by a statistical model called a random coefficient model.

For multilevel data, where observations are nested within clusters (e.g. household, region), mixed-effects regression models (aka multilevel or hierarchical linear models) are often used to account for the dependency inherent in the data [24]. Models for ordinal outcomes often include the proportional odds assumption for model covariates. For an ordinal response with J categories, this assumption states that the effect of the covariate is the same across the J-1 cumulative logits of the model (or proportional across the cumulative odds).

Testing heterogeneous proportions

The most commonly used test statistic to check for heterogeneity of proportion between groups (regions) which is the proper application of multilevel analysis is the chi-square test statistic.

To test whether there are indeed systematic differences between the groups (regions), the chi-square test can be used.

$X^2={\displaystyle \sum }_{k=1}^{11}{n}_k\frac{n_k{({\stackrel{-}{Y}}_{.k}-{\hat{P}}_{.})}^2}{{\hat{P}}_{.} (1-{\hat{P}}_{.})}$

Where is group average obtained as ${\stackrel{-}{Y}}_{.k}=\frac{{{\displaystyle \sum }}_{i=1}^{n_k}{Y}_{ik}}{n_k}$ is the proportion of successes in group k (k is the number of regions (i.e. 11)) which is an estimate for the group-dependent probability p_j and $\widehat{p}$ . is the overall average. i.e. the overall proportion of successes. The decision is based on a chi-square distribution with k-1 degrees of freedom [25].

Random intercept only model

The empty level-2 model for an ordinal response variable refers to a population of groups (level-two units, i.e. regions) and specifies the probability distribution for group dependent probabilities Pj without taking further explanatory variables into account. Therefore, in this situation with three categories of response, there are two logits and their corresponding intercepts simultaneously estimated, each of them indicating the probability of responding in or below a particular category. This model only contains random groups and random variations across the regions. The equations are necessary for estimating this model are presented below.

${\gamma }_{ik1}=logit\left(\frac{P(Y_{ik}\le 1)}{1-P(Y_{ik}\le 1)}\right)={\beta }_0+u_{ok}$

${\gamma }_{ik2}=logit\left(\frac{P(Y_{ik}\le 2)}{1-P(Y_{ik}\le 2)}\right)={\beta }_0+u_{ok}+{\delta }_k$

Where, γ_ikj are the cumulative probabilities of the j^th categories of the response variable in i^th level-1 nested in k^th level-2, $\delta k$ is the difference between the two response categories, and where, ${\beta }_0$ is the average of the ordered outcome variable (intercept) of the transformed probabilities and the random deviation from this average for group k.

Random intercept model

In the random intercept logistic regression model, the intercept is the only random effect meaning that the groups differ with respect to the average value of the response variable. It represents the heterogeneity between groups in the overall response. When dealing with ordinal response outcomes, multiple logits are simultaneously estimated (J-1 logits, where J = the number of response categories). Hence, in this situation with three categories of response, there will be two logits and their corresponding intercepts simultaneously estimated, each of them indicating the probability of responding in or below a particular category. The equations essential for estimating these models are shown below.

${\gamma }_{ik1}=logit\left(Y_{ik}\le 1\right)=log\left\{\frac{P(Y_{ik}\le 1)}{1-P(Y_{ik}\le 1)}\right\}={\beta }_{0k}+{\beta }_{1k}{x}_{1ik}+{\beta }_{2j}{x}_{2ik}+\dots +{\beta }_{qk}{x}_{qik}$

$={\beta }_{0j}+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qik}$

${\gamma }_{ik2}=logit\left(Y_{ik}\le 2\right)=log\left\{\frac{P(Y_{ik}\le 2)}{1-P(Y_{ik}\le 2)}\right\}={\beta }_{0j}+{\beta }_{1k}{x}_{1ik}+{\beta }_{2j}{x}_{2ik}+\dots +{\beta }_{qk}{x}_{qik}$

$={\beta }_{0k}+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qik}+{\delta }_j$

Where, γ_ij are the log odds of being at or below the j_th categories of the birth weight of babies i in regions k, Q is a total number of covariates at level-1. More specifically, ${\gamma }_{ik1}$ corresponds to the log odds of being at or below the first categories of the response variable (low birth weight) of baby i in region j and ${\beta }_{0k}$ is the intercept or the average log odds of being at or below the j categories, x_ik is the level-1 predictor for baby i in region k, and represents the slope associated with. Similarly, ${\gamma }_{ik2}$ represents the log odds of being at or below the second category of the response variable (normal birth weight) for baby i in region k. In this case, ${\beta }_{0k}$ the intercepts term (threshold) is assumed to vary randomly across the region, and the difference between the logits remains fixed across the region, and is given by the sum of an average intercept ${\beta }_0$ and group-dependent deviations u_ok. i.e ${\beta }_{0k}={\beta }_0+u_{ok}$. Then,

${\gamma }_{ik1}=logit\left(Y_{ik}\le 1\right)={\beta }_0+{\displaystyle \sum }_{k=1}^K{\beta }_{qk}{x}_{qik}+u_{ok}$

${\gamma }_{ik2}=logit\left(Y_{ik}\le 2\right)={\beta }_0+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qik}+u_{ok}+{\delta }_k$

Note that the first part of the left-hand side incorporates the regression coefficients in both equations ${\beta }_0+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qik}$ is the fixed part of the model, because the coefficients are fixed. The remaining part $u_{ok}$ is called the random part of the model. It is assumed that the residual, u_ok are mutually independent and normally distributed with mean zero and variance ${\sigma }_0^2$ The above equation is considered a mixed model because it has both fixed effects and random effects [23].

Random coefficient model

In the random intercept logistic regression model, the intercept is the only random effect meaning that the groups differ with respect to the average value of the dependent variable. But we have assumed that the effects of the explanatory variables are the same for each region. This assumption is considered by allowing the difference between explanatory variables within a region to vary across regions. To allow for this effect, we will need to use a random coefficient for those explanatory variables. So, the random coefficient model represents heterogeneity in the relationship between the response and explanatory variables. As stated above the response variables in the study, birth weight of babies is an ordinal variable and the statistical model employed is the two-level random coefficient logistic regression model. The model, with level-1 predictors and level-2 predictors, can be expressed as:

${\gamma }_{ik1}=logit\left(Y_{ik}\le 1\right)=log\left\{\frac{P(Y_{ik}\le 1)}{1-P(Y_{ik}\le 1)}\right\}={\beta }_{0k}+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qik}+{\displaystyle \sum }_{p=1}^P{u}_{pk}{x}_{pik}$

${\gamma }_{ik2}=logit\left(Y_{ik}\le 2\right)=log\left\{\frac{P(Y_{ik}\le 2)}{1-P(Y_{ik}\le 2)}\right\}={\beta }_{0k}+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qikj}+{\displaystyle \sum }_{p=1}^P{u}_{pk}{x}_{pik}+{\delta }_k$

Where, ${\beta }_{0k}={\beta }_0+u_{0k}, u_{ok}~N\left(0,{\sigma }_0^2\right) , u_{pk}~N(0,{\sigma }_p^2)$ , P is the total number of covariates at level-2.

Now the above equation is written as:

${\gamma }_{ik1}=logit\left(Y_{ik}\le 1\right)=log\left\{\frac{P(Y_{ik}\le 1)}{1-P(Y_{ik}\le 1)}\right\}={\beta }_0+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qik}+u_{0k}+{\displaystyle \sum }_{p=1}^P{u}_{pk}{x}_{pik}$

${\gamma }_{ik2}=logit\left(Y_{ik}\le 2\right)=log\left\{\frac{P(Y_{ij}\le 2)}{1-P(Y_{ij}\le 2)}\right\}={\beta }_0+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qikj}+u_{0k}+{\displaystyle \sum }_{p=1}^P{u}_{pk}{x}_{pik}+{\delta }_k$

In the first part of both equations, ${\beta }_0+{\displaystyle \sum }_{q=1}^Q{\beta }_{qk}{x}_{qikj}$ , is called the fixed part of the model and the second part of both equations, $u_{0k}+{\displaystyle \sum }_{p=1}^P{u}_{pk}{x}_{pik}$ is called the random part [23].

Interclass correlation

Interclass Correlation (ICC) is the degree of resemblance between level one units belonging to the same group. It is an indication of the proportion of variance at the second level (region) and it can also be interpreted as the expected (population) correlation between two randomly chosen individuals within the same group (Joop, 2010).

In two- the level model, the ICC is calculated from the intercept-only model. This model can be derived from the empty model/ random intercept only model by excluding all explanatory variables, which results in the following equation: S

$\text{ICC }=\frac{{\sigma }_u^2}{{\sigma }_u^2+{\sigma }_e^2}\text{ (3}\text{.9)}$

Where, ${\sigma }_e^2\mathfrak{M}$ is the variance of baby (lower) level units. For a logistic regression model (either binary or ordinal), the level-1 variance is not estimated. Since the logistic distribution for the level one residual variance implies a variance of $\frac{{\pi }^2}{3}$ (that is 3.29) (Snijders and Bosker, 1999) and this formula can be reformulated as:

$\text{ICC }=\frac{{\sigma }_{u0}^2}{{\sigma }_{u0}^2+3.29}$

Results

Descriptive statistics

Out of a total of 8,328 babies, 1292 (15.5%) were LBW, 6143(73.8%) were normal birth weight and 893 (10.7%) were HBW at the time of the survey. The proportion of the birth weight of babies was differing by age of the mother. Accordingly, the LBW baby whose age of their mother was between 35-39 had the highest proportion (3.2%), followed by 30-34 (2.9%). The lowest proportion of LBW babies was observed among 15-19 (0.2%), followed by 20-24(1.2%). The highest proportion of normal birth weight was recorded at 35-39 (16.5%), followed by 30-34 (15.4%). The lowest proportion of normal birth weight was 15-19 (0.1%), followed by 20-24 (5.4%). Also, Table 1 showed that the highest proportion of HBW babies was recorded at 35-39(2.5%) and the lowest was 15-19(0.1%).

The proportion of the birth weight of babies is varying across the regions. The highest proportion of LBW babies was recorded in the Afar region (1.9%) and followed by the Amhara region (1.8%). Harari has the lowest proportion of LBW (0.9%), followed by Somali (1%). The highest proportion of normal birth weight babies was recorded in the Oromia region (9.1%) and followed by the SNNP region (8.7%). Harari has the lowest proportion of normal birth weight (4.8%), followed by Afar (4.9%). The highest proportion of HBW babies was recorded in the Oromia region (1.4%), followed by Addis Ababa (1.3%). Afar has the lowest proportion of HBW (0.4%), followed by Harari (0.6%).

Also, the proportion of birth weight differed by place of residence. Accordingly, among babies whose residence of their family was rural area 10.9% was LBW, 52% was normal and 8% were HBW. Similarly, among babies whose residence of their family was urban area 4.6% was LBW, 21.8% was normal and 2.7% was HBW.

Additionally, the proportion of birth weight among babies also varies among the gestational ages (in weeks). The LBW babies whose gestational age was pre-term, term, and post-term were representing 6%, 8.8%, and 0.8% respectively. Likewise, the normal birth weight babies who are their gestational age were pre-term, term, and post-term representing 15.1%, 48.5%, and 10.1% respectively. Also, the HBW babies whose gestational age was pre-term, term, and post-term represented 0.6%, 5.2%, and 4.9% respectively.

Moreover, Table 1 revealed that single pregnancy and multiple pregnancy babies who were LBW represented 9.5% and 6%, respectively. The proportion of single and multiple pregnancy babies who were normal birth weight represented 69.2% and 4.6% respectively. The proportion of single and multiple pregnancy babies who were HBW was represented at 10.5% and 0.2% respectively. Table 1 also found that male and female babies who have LBW represented 8.3% and 7.2%, respectively. The proportion of male and female babies who have normal birth weight represented 37.6% and 36.1% respectively. The proportion of male and female babies who have HBW represented 6.7% and 4% respectively.

According to Table 1, the last column indicates the association between the response variable with all predictors variables which revealed that there is a statistically significant association between the birth weight of babies and mother age, region, residence, maternal age at 1^st birth, wealth index, BMI, gestational age, anemia level, smoking cigarette, total children mother delivery, multiple pregnancies, birth order and sex of baby at 5% level of significance. However, marital status, religion, mother educational level, husband educational level, and ANC visits during pregnancy had no statistical association with the birth weight of babies at a 5% level of significance.

Multilevel ordinal logistic regression analysis

In this study, a multilevel ordinal logistic regression model was employed to compare the existence of variation with regard to the levels of birth weight of babies among regions. There were 11 regions that have been included as the second-level units. A total of 8,328 babies were considered as first-level units. The empty model with random intercepts, the random intercept with fixed effects model, and the random coefficient with the random coefficient model have been considered and model comparison, testing goodness of fit, and interpretation of fixed effects in terms of odds ratio are presented.

Test of parallel lines assumption

In ordinal logistic regression models, there is an assumption that belongs to ordinal odds. According to this assumption, parameters should not change for different categories. In other words, location parameters (slope coefficients) are the same across response categories. Equality of the following hypothesis shows that the test whether coefficients of the independent variable are equal or not for every single category. $\text{Ho}={\beta }_{1j}={\beta }_{2j}=\dots ={\beta }_{(k-1)j}$ where j = 1, 2, 3,…, J versus H1: at least one ${\beta }_j$ is different and k represents parameters or slope coefficients across categories. As displayed in Table A2 in Appendix A, the researcher does not reject the null hypothesis at a 5% level of significance. This shows that there is no sufficient evidence to reject the null hypothesis, indicating that the parameters (slope coefficients) are the same across response categories.

Test of heterogeneity

Before preceding the proper application of multilevel analysis first the researcher has to test for heterogeneity of proportions between regions. The chi-square test was applied to assess heterogeneity among regions. As shown in Table A3 in Appendix A, the chi-square test is yields x2 = 36.159 with d.f 20 (P = 0.015). Thus, there is evidence of heterogeneity among the regions with respect to the birth weight of babies in Ethiopia.

Random intercept only model

The researcher first considers a random intercepts only model in order to examine the variation due to the regional effects and predict the probability of the baby being LBW versus the combined categories namely normal birth weight and HBW or the probability of the baby being LBW and normal birth weight versus HBW in Ethiopia, while controlling the other independent variables constant.

As shown in Table 2, the log-odds of being LBW versus the combined categories of normal and HBW given in all regions under investigation, on average, were estimated as ${\beta }_{01}$ = -2.0870. Likewise, the log odds of being LBW and normal versus the HBW category given in all regions under investigation, on average, were estimated as ${\beta }_{02}$ = 2.1320.

Additionally, the between-region intra-class correlation coefficient (ICC) obtained from the empty model with random intercepts was (0.5117)/ (.5117+3.29) = .135. This ICC value is interpreted as about 13.5% of the variation in the birth weight can be explained by grouping the babies with respect to their regions. The remaining value, 86.5%, of the variation in birth weight can be explained within individuals (level-1 units, i.e. babies) or within the regional variation of birth weight.

The likelihood ratio statistic for testing the null hypothesis, that ${\sigma }_{uo}^2$ = 0, can be calculated by comparing the level-2 ordinal model, with the corresponding single-level ordinal model or the standard logit model. Depend on the log link = -5609.3 of two-level empty model and logLik = -5612.4 of single-level empty model from result of Table A4 in Appendix A, the difference is -2*logLik (single-level) – (-2*logLik (two-level)) = 6.1832. The test statistic is (X²= 6.1832) with 1 degree of freedom and rejects the null hypothesis at a 0.05 level of significance, so there is strong evidence that between region variance is non-zero. This shows that the birth weight of babies is varying among regions and adding the random intercepts or between-region variance in the model is necessary in order to detect the effect of the birth weight of babies among regions. Also, as shown in Table A4 in Appendix A, the value of AIC for a null model with random effect, (AIC = 11224.6) was less than for the null model without random effect (AIC = 11228.8), showing that the null model with random effect (in case of multilevel) was better than the null model without random effect (in case of single-level).

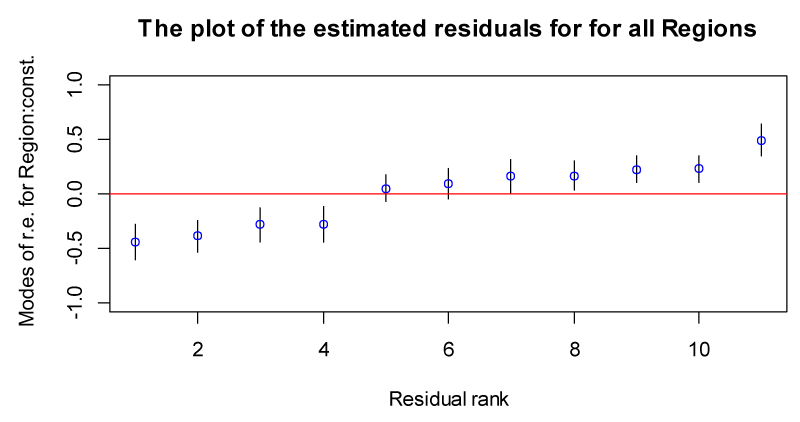
Now researcher examines estimates of the region effects or residuals, ${\widehat{u}}_{oj}$ obtained from the null model. To calculate the residuals and produce a caterpillar plot with the region effects shown in rank order together with 95% confidence intervals Figure 1.

Plot 1 shows the estimated residuals for all 11 regions in the sample. The residuals represent regional departures from the overall mean, so a region whose confidence interval does not overlap the line at zero (representing the mean value of the birth weight of the baby across all regions) is said to differ significantly from the average at the 5% significance level. On the lower side of the plot, there is a cluster of regions whose mean birth weight of the baby was lower than average and vice versa.

Random intercept with fixed slope model

To assess the effect of the independent variables on the birth weight of a baby with respect to its categories, the researcher considered a random intercept with a fixed slope model. In random intercept with a fixed slope model, all predictors (level-1 covariates) are included. But, the effect of each predictor is assumed to be the same in each region. The probability of babies being LBW versus the combined categories namely normal and HBW and the probability of babies being LBW and normal versus HBW is allowed to vary across regions while level-1 covariates including the fixed intercept are fixed or constant across regions.

According to the result in Table 3 the random intercept with the fixed slope model, the fixed part showed that the mother’s age, residence, maternal age at birth, wealth index, anemia level, BMI, gestational age, parity, multiple pregnancies, and baby’s sex were found to be significant factors associated with birth weight in all regions with respect to the corresponding reference categories.

The result in Table 3 also showed that the inclusion of level-one covariates reduced region variations from 0.5119 (level-two variance without covariates) to 0.3216 (level-two variance with level-1 covariates). The 95% C. I for region variance does not include zero. This leads to the rejection of the null hypothesis that the random effect is zero. From this, the researcher concluded that there is a significant variation between regions in levels of birth weight of babies.

The result in Table 3 revealed that the intra-class correlation coefficient (ICC) is 0.3216/ (0.3216+3.29) = 0.089. This value is called the intra-class correlation coefficient (ICC) and is interpreted as 8.9% of the variation in levels of birth weight of babies is due to differences across the regions, with the remaining unexplained 91.1% variation attributable to individual (babies) differences.

Random coefficient model

In random intercept with a fixed slope model, the researcher allowed the probability of a baby’s birth weight to vary across regions by assuming that the effects of all explanatory variables in the study are the same//uniform for each region. In this model, the researcher is going to see the effect of level-1 covariates by allowing them to vary randomly across regions. The researcher tests the effects of all significant variables step by step whether they have a random effect across the region or uniform. However, among all significant covariates in the study, only the effect of maternal age at 1^st birth and wealth index varies across regions. So, in the random coefficient model, the researcher needs to introduce a random slope of mother age at 1^st birth and wealth index to vary randomly across the regions Table 4.

The goodness of fit test

Before interpreting multilevel models, the researcher compares the three multilevel ordinal logistic regression models. The deviance and AIC criteria were used to select the best model among the three fitted two-level ordinal logistic regression models for the data under consideration.

As shown in Table 5, the deviance of the null model is 11,224.6 and for random intercept with a fixed slope model is 10,995.2. This shows that random intercepts with a fixed slope model were better than the null model. The deviance of the random coefficient model (deviance = 10,977.4) shows that the random coefficient model was better than the random intercept with a fixed slope model.

AIC was used to make an overall comparison of the three models. For levels of birth weight, the computed AIC value for the null model (AIC = 11,244.6) was greater than for the random intercept with the fixed slope model (AIC = 11,047.9). This indicates that the random intercept with the fixed slope model was a better fit as compared to the null model with a random intercept. The value of AIC for random intercepts with a fixed slope model (AIC = 11,047.9) was greater than for the random coefficient model, (AIC = 11,039.4), showing that the random coefficient model is the best model to fit data under consideration compared with random intercept with fixed slope model. Therefore, the random coefficient multilevel ordinal logistic regression model is the best model to fit data for this study and further interpretation, conclusion, and recommendation would depend on the results of this model.

Interpretation of the results of the random coefficient model

From the result of the parallel line assumption test, the likelihood of being at or below the J-1 categories of birth weight has the same odds ratio across the response categories. Accordingly, the odd of being LBW versus the combined categories of normal birth weight and HBW has the same interpretation as the odd of being LBW and normal birth weight versus HBW, given any variable in the study held constant.

The intercept ${\beta }_{01} and {\beta }_{02}$ are called the grand mean that is shared by all regions. Based on Table 4. the thresholds/cut points reveal that the log-odds of being LBW given in all regions under investigation, on average, were estimated as ${\beta }_{01}$ = -1.7931. Likewise, the log odds of being at or below normal birth weight given in all regions under investigation, on average, were estimated as ${\beta }_{02}$ = 2.5567.

Additionally, the intra-class correlation coefficient or between regions variations in the random coefficient model decreased by 3.2% as compared to the empty random intercept model. This value implied that only 10.3% [0.3791/ (0.3791+3.29) = 0.103] of the variation in the birth weight of babies can be explained by the difference across the regions. The remaining value, 7.2%, 5.6%, and 76.9% of the variation in birth weight of babies can be explained mother's age at 1^st birth, wealth index and within individuals (level-1 units, i.e. babies) respectively.

The results of the fixed part of the random coefficient model show that maternal age, residence, maternal age at 1^st birth, wealth index, BMI, gestational age, anemia level, total children mother delivery, multiple pregnancies, and sex of baby were statistically significant determinants of variation in birth weight of babies in all regions with respect to the corresponding categories.

Accordingly, the odd of mother age lies between 25-29 and 35-39 years born LBW babies versa the combined categories of normal birth weight and HBW were 11.82% [OR = 0.8818, CI = 0.6283,0.8050] and 41.48% [OR = 0.5852, CI = -0.7133,-0.3581] less as compared to mother age lies between15-19 years respectively, while holding other variables in the model constant. Similarly, the odd of mother age lies between 25-29 and 35-39 years born LBW and normal babies versa HBW were 11.82% [OR = 0.8818, CI = 0.6283,0.8050] and 41.48% [OR = 0.5852, CI = -0.7133,-0.3581] less as compared to mother age lies between15-19 years respectively, while holding other variables in the model constant.

The odd of babies from the rural area being LBW versa the combined categories of normal and HBW babies was 37.2% [1.3720, CI = 1.0739, 1.7529] more than compared to an urban area while holding other variables in the model constant. Similarly, the odd of babies from the rural area being LBW and normal versa HBW babies was 37.2% [1.3720, CI = 1.0739, 1.7529] more than compared to the urban area while holding other variables in the model constant.

Also, the results show that the odd of maternal age at 1^st birth lies between 20-34 years born LBW versa the combined categories of normal and HBW babies was 29.31% [OR = 0.7069, CI = -0.3886,-0.3052] less than as compared to maternal age at 1^st birth lies below 20 years while holding other variables in the model constant. Likewise, the odd of maternal age at 1^st birth lies between 20-34 years born LBW and normal babies versa HBW babies was 29.31% [OR = 0.7069, CI = -0.3886,-0.3052] less than as compared to maternal age at 1^st birth lies below 20 years while holding other variables in the model constant.

Additionally, the odd of mothers whose wealth index is poor, middle, rich, and richest born LBW babies versa the combined categories of normal and HBW babies was 36.51%, 46.72%, 65.09%, and 65.48% less than as compared to poorest respectively while holding other variables in the model constant. Likewise, the odds of mothers whose wealth index is poor, middle, rich, and richest born LBW and normal babies versa HBW babies was 36.51%, 46.72%, 65.09%, and 65.48% less than compared to poorest respectively while holding other variables in the model constant.

The results also reveal that the odds of a mother who had obese BMI born LBW babies versa the combined categories of normal and HBW babies was 24.15% [OR = 0.758, CI = 0.5827, 0.9873] less than compared underweight while holding other variables constant. Similarly, the odds of a mother who had an obese BMI born LBW and normal babies' versa HBW babies was 24.15% [OR = 0.758, CI = 0.5827, 0.9873] less than compared underweight, while holding other variables constant.

Additionally, the odds of babies whose gestational age is LBW versa the combined categories of normal and HBW was 5.12% [OR = 0.8488, CI = 0.7721, 1.0431] and 53.76% [OR = 0.4624, CI = 0.3728, 1.7435] less than as compared to pre-term respectively while holding other variables constant. Likewise, the odds of babies whose gestational age is LBW and normal versa HBW was 5.12% [OR = 0.8488, CI = 0.7721, 1.0431] and 53.76% [OR = 0.4624, CI = 0.3728, 1.7435] less than as compared to pre-term respectively while holding other variables constant.

The odd of a mother who had mild anemia gives LBW babies versa the combined categories of normal and HBW babies was 22.73% [OR = 0.7727, CI = 0.6132, 0.9736] less than as compared to non-anemic while holding other variables constant. Similarly, the odds of a mother who had mild anemia giving LBW and normal babies and versa HBW babies was 22.73% [OR = 0.7727, CI = 0.6132, 0.9736] less than compared to non-anemic, while holding other variables constant.

The odds of a mother who delivers more than one child giving LBW babies versa the combined categories of normal and HBW babies was 46.92% [OR = 1.4692, CI = 1.1363, 1.8993] more than compared to mother who delivered only one child while holding other variables in the model constant. Likewise, the odds of a mother who delivered more than one child giving LBW and normal babies and versa HBW babies was 46.92% [OR = 1.4692, CI = 1.1363, 1.8993] more than compared to mother who delivered only one child, while holding other variables in the model constant.

The odds of multiple pregnancies of women delivering LBW babies versa the combined categories of normal and HBW babies was 28.65% [OR = 0.7135, CI = 0.5116, 0.9952] less than as compared to single pregnancy while holding other variables in the model constant. Likewise, the odds of multiple pregnancies for women delivering LBW and normal babies and versa HBW babies was 28.65% [OR = 0.7135, CI = 0.5116, 0.9952] less than compared to single pregnancy, while holding other variables in the model constant.

The odd ratio for females was 1.1373 [CI = 1.0221, 1.2655]. This indicates that the likelihood of female babies being LBW was 13.73% more than compared to male babies while holding other variables in the model constant.

In the random effect part, the value of 0.1946, 0.2252, and 0.3791 are the estimated variance of intercept, the slope of wealth index, and slope of mother age at 1^st birth respectively. These estimated variances, intercept, the slope of wealth index and slope of mother age at 1^st birth are significant variations across the region. So, there is a significant variation in the effect of wealth index and mother age at 1^st birth across regions in Ethiopia.

The positive correlation estimate (0.1004) between the slope of wealth index and slope of mother age at 1^st birth indicated that regions with the high slope of wealth index/slope of mother age at 1^st birth tend to have on the average higher slope of mother age at 1^st birth/slope of wealth index respectively. The negative correlation estimate (-0.418,-0.039) between intercept with the slope of wealth index and slopes of mother age at 1^st birth, respectively, suggest that regions with a high intercept (above-average) tend to have on average higher slopes. In general, a Positive correlation between intercepts and slopes implies that regions with the higher intercepts tend to have on average higher slopes and the negative sign for the correlation between intercepts and slopes implies that regions with the higher intercepts tend to have on average lower slopes on the corresponding predictors.

Model diagnostic

The diagnostic plot for residuals like Pearson and standardized residuals of the multilevel model is presented in Appendix B. The scatter plot of the multilevel model presented under Appendix B verifies that the residual of the model versus index or residual versus the estimated probability did not show any systematic pattern. This suggested that the residuals are symmetric around zero (i.e. positive and negative residuals are almost equal). For acceptable fit, one would expect that locally the residual average is zero, the smooth line helps in detecting a deviation from this expectation. Therefore, from these residual plots, the model fit is very well. Thus, the fitted multilevel ordinal logistic regression model is a good fit for the given data.

Discussions

This study intended to identify the regional difference and factors associated with the birth weight of babies in Ethiopia. Descriptive analysis, chi-square test, and multilevel ordinal logistic regression analyses were used in this study. This study found that some of the demographic, socio-economic, and health-related variables have a significant relation to the birth weight of babies and compare the results of this study with the studies in literature as followed.

The descriptive result showed that the proportion of LBW was 15.5%. This was relatively in line with a study in South Africa (13.7%), Sub Sahara Africa (14%), Angola (15.3%), Gabon (16.8%), Madagascar (17.1) WHO [1] and in Dessie town (15.6%) Abebaw [15]. But, it is higher than some studies like in Nigeria (7.3%) Dahlui (2016), and Western Europe (6.9%) [1]. This study also found that the proportion of LBW was higher than the report of 2011 EDHS (11%) [26]. On the other hand, the results of this study found that the proportion of HBW was 10.7% which is relatively consistent with the studies in Ghana (9.69%) [27] and in Hawassa (11.86%) [21]. But, it is higher than the study in Tanzania (2.3%) [14]. Additionally, the study shows that the proportion of LBW was higher than HBW, and this may also be due to many respondents included in this study being from the rural area which increases the rate of LBW. Because, in the rural area most pregnant women have underweight, no follow-up during pregnancy, and no more education on the birth weight of their babies.

The results of multilevel ordinal logistic regression analysis revealed that maternal age, place of residence, maternal age at 1^st birth, wealth index, BMI, gestational age, anemia level, total children mother delivery, multiple pregnancies, and sex of baby were found to be significant factors associated with a birth weight of babies in Ethiopia.

Accordingly, the results showed that the mother's age was the most risk factor associated with the birth weight of babies. It indicates that the risk of LBW babies was higher among women at an early age. This could be due to the fact that this age group is physical and emotionally immature and their bodies are unable to withstand the stress of pregnancy, while, the risk of HBW baby was higher among older women. This may be due to older women having strong and mature bodies that enable them to withstand the stress and complication during pregnancy. This finding is consistent with the studies [15,17,28]. However, this study is inconsistent with the articles [29,30]. This may be due to the researcher using a multilevel model by handling the level-2 effect in the model.

The findings of this study also showed that the residence of the mother was the most important factor in the birth weight of babies. Babies whose their family is lived in rural areas were more likely to get LBW than in urban areas. In rural areas no more education that leads women to follow up in health centers during pregnancy, no earlier prevention and detective from anemia, underweight, and no balanced diet like iron, vitamin, and weight gain during pregnancy for lower-class economic women. On other hand, babies whose families are lived in urban areas are more likely to get HBW than in rural areas. This may be due to most of the urban women being overweight and having a balanced diet. This result is in line with the finding of the study [15,19,31].

The results of this study also found that the wealth index was significantly affecting the birth weight of babies. The babies who are their family economic class were lower have a high probability to get LBW and higher economic status have a high probability to get HBW. Malik, et al. [13] and Manyeh, et al. [28] used binary logistic regression to analyze factors associated with HBW, being lower economic class was associated with LBW and the higher economic class was associated with HBW which is in line with the results of this study.

The finding of this study also revealed that the Body Mass Index of the mother is the main factor associated with the birth weight of babies. Abubakari, et al. [31] conducted binary logistic regression in order to analyze the risk factor associated with birth weight in Iraq, being underweight was the risk factor for LBW, while the overweight and obese mother was associated with HBW. Mothers whose BMI was obese were more likely to birth HBW than other mothers. The results of this study are consistent with studies [19,31,32].

Moreover, Gestational age plays an important role in determining the birth weight of babies. Babies who are delivered prematurely (< 37 weeks) are at higher risk to have a low birth weight of babies. It is evident that preterm births are exposed to LBW due to inadequate weight gain during pregnancy because of early delivery. The World Health Organization estimated about one-third of low birth weight babies are caused by prematurity [1]. On the other hand, babies who are delivered post maturely (> 40 weeks) are at higher risk to have HBW. This may be attributable to the period of post-maturity that there could lead to excessive fetal weight gain. According to our findings, as compared with pre-term gestational age, the risks of being LBW babies and HBW in pre-term and post-term gestational age were highly significant respectively. This is consistent with the previous studies [14,31,32].

Also, our findings revealed that anemia level was one of the most factors associated with the birth weight of babies. The results of this study found that mothers who have mild anemia were significantly associated with LBW than non-anemic mothers. This might be because of that micronutrient deficiency during pregnancy had been shown to have serious implications on the developing fetus and during pregnancy, women become to lose weight and feels very weak and tired. This is in line with AbdalQader, et al. [33] conducted binary logistic regression to analyze risk factors associated with LBW babies in Iraq, and revealed that women who have anemia have a higher risk to give LBW babies than non-anemia women. Also, this study is consistent with studies [18,20].

Furthermore, multiple pregnancies were significantly affecting the birth weight of babies. This could be because of multiple pregnancies women have highly probably of having LBW babies. This is consistent with the studies [10,32,34].

The results also show the sex of the baby was the most factor associated with the birth weight of babies. This means that being male was highly HBW. There may be biological reasons which could expose male babies to excessive weight gain during pregnancy. While being female was associated with LBW. This is in line with the previous studies [10,17,28,32].

According to this finding total number of children mothers ever born was a significant factor associated with the birth weight of babies which is inconsistent with the study [35]. However, maternal age at 1^st birth was a significant factor associated with the birth weight of babies which is inconsistent with the studies [21,36]. This may be due to the use of binary logistic regression that considers only fixed effects to analyze the factors associated with the birth weight of babies. However, the researcher considered both fixed and random effect that makes the difference between the significance of this variable in this study and other studies [37-57].

The multilevel ordinal logistic regression model allows for the comparison of variations between regions. Before the analysis of data using the multilevel approach, heterogeneity of the levels of birth weight in the region was first checked using the chi-square test and it was significantly shown that there is regional heterogeneity regarding the birth weight of babies. Results obtained based on the empty model the overall variance of the constant term suggests that the birth weight of babies differed across regions. In addition to this, the random coefficient model was the best model to fit the data under consideration and to assess the regional variation and factors associated with the birth weight of babies. The random coefficient model showed that the effect of maternal age at 1^st birth and wealth index were random across regions in explaining the birth weight.

The multilevel ordinal logistic regression analysis revealed that the maternal age, residence, maternal age at 1^st birth, wealth index, BMI, anemia level, gestational age, total children mother delivery, multiple pregnancies, and sex of baby were significant factors associated with a birth weight of babies. In addition to that, the results of a non-parametric approach based on the chi-square test and the parametric approach based on the multilevel ordinal logistic regression model without explanatory variables (empty model) suggest that the proportion of the birth weight of babies was significantly varied among the regions. The results of the model comparison of the three multilevel ordinal logistic regression models show that the random coefficient multilevel model provided the best fit for the data under consideration.

Similarly, the results of the study show that the effects of (mother age, residence, BMI, anemia level, gestational age, total children mother delivery, multiple pregnancies, and sex of baby) were uniform throughout the regions. However, the effects of mother age at 1^st birth and wealth index were random across the regions. Therefore, it is possible to conclude, that maternal age at 1^st birth and wealth index has a random effect that is responsible for explaining the variation in birth weight of babies between regions of Ethiopia.

Ethics approval and consent to participate

Data for the 2016 EDHS was collected from January 18 to June 27, 2016. The survey protocol was jointly evaluated and approved by Ethiopia's Ministry of Science and Technology and ICF International's Institutional Review Board. Each responder above the age of 18 gave their written consent, while all adolescents under the age of 18 gave their written informed consent, and parents or guardians of participants under the age of 18 gave their written informed consent. Any participant identifiers are erased during data input activities before data management and analysis in any DHS study. The authors obtained permission to conduct the current analyses from the MEASURE DHS website, which is open to the public.

Appendix-A,B

1. World Health Organization. UNICEF-WHO low birthweight estimates: levels and trends 2000-2015 (No. WHO/NMH/NHD/19.21). United Nations Children’s Fund (‎‎ UNICEF)‎‎. 2019.
2. Henriksen T. The macrosomic fetus: a challenge in current obstetrics. Acta Obstet Gynecol Scand. 2008;87(2):134-45. doi: 10.1080/00016340801899289. PMID: 18231880.
3. Ye J, Torloni MR, Ota E, Jayaratne K, Pileggi-Castro C, Ortiz-Panozo E, Lumbiganon P, Morisaki N, Laopaiboon M, Mori R, Tunçalp Ö, Fang F, Yu H, Souza JP, Vogel JP, Zhang J. Searching for the definition of macrosomia through an outcome-based approach in low- and middle-income countries: a secondary analysis of the WHO Global Survey in Africa, Asia and Latin America. BMC Pregnancy Childbirth. 2015 Dec 3;15:324. doi: 10.1186/s12884-015-0765-z. PMID: 26634821; PMCID: PMC4669645.
4. Madoue G, Nguele Sile S, Lhagadang F, Saleh A. HBW : risk factors, maternal and fetal outcome in N’Djamena mother and child hospital, Chad. Obstet Gynecol Int J. 2018; 9(3), 153α155.
5. Koyanagi A, Zhang J, Dagvadorj A, Hirayama F, Shibuya K, Souza JP, Gülmezoglu AM. Macrosomia in 23 developing countries: an analysis of a multicountry, facility-based, cross-sectional survey. Lancet. 2013 Feb 9;381(9865):476-83. doi: 10.1016/S0140-6736(12)61605-5. Epub 2013 Jan 4. PMID: 23290494.
6. Luhete PK, Mukuku O, Kiopin PM, Tambwe AM, Kayamba PK. HBW  in Lubumbashi: risk factors and maternal and perinatal prognosis. The Pan African medical journal. 2016; 23: 166-166.
7. Rao J, Fan D, Wu S, Lin D, Zhang H, Ye S,  Zhang J. Trend and risk factors of low birth weight and macrosomia in south China, 2005–2017: a retrospective observational study. Scientific reports. 2018; 8(1): 1-8.
8. Ahankari A, Bapat S, Myles P, Fogarty A, Tata L. Factors associated with preterm delivery and low birth weight: a study from rural Maharashtra, India. F1000Res. 2017 Jan 24;6:72. doi: 10.12688/f1000research.10659.1. PMID: 28529697; PMCID: PMC5428483.
9. Aboye W, Berhe T, Birhane T, Gerensea H. Prevalence and associated factors of low birth weight in Axum town, Tigray, North Ethiopia. BMC Res Notes. 2018 Oct 1;11(1):684. doi: 10.1186/s13104-018-3801-z. PMID: 30285895; PMCID: PMC6167810.
10. Chibwesha CJ, Zanolini A, Smid M, Vwalika B, Phiri Kasaro M, Mwanahamuntu M, Stringer JS, Stringer EM. Predictors and outcomes of low birth weight in Lusaka, Zambia. Int J Gynaecol Obstet. 2016 Sep;134(3):309-14. doi: 10.1016/j.ijgo.2016.03.021. Epub 2016 Jun 9. PMID: 27365291; PMCID: PMC4987240.
11. Abdo RA, Endalemaw TB, Tesso FY. Prevalence and associated factors of adverse birth outcomes among women attended maternity ward at Negest Elene Mohammed Memorial General Hospital in Hosanna Town, SNNPR, Ethiopia. J Women’s Health Care. 2016; 5(4).
12. Najafian M, Cheraghi M. Occurrence of fetal macrosomia rate and its maternal and neonatal complications: a 5-year cohort study. ISRN Obstet Gynecol. 2012;2012:353791. doi: 10.5402/2012/353791. Epub 2012 Nov 14. PMID: 23209925; PMCID: PMC3504382.
13. Malik M, Khanna P, Verma R. The association of maternal risk factors to macrosomia in rural areas of Haryana, India: a community based study. International Journal of Community Medicine and Public Health. 2018; 5(9): 3842.
14. Said AS, Manji KP. Risk factors and outcomes of HBW  in a tertiary centre in Tanzania: a case-control study. BMC pregnancy and childbirth. 2016; 16(1): 243.
15. Abebaw D. Prevalence and Associated Factors of Low Birth Weight Among Newborn Babies in Dessie Town Health Institutions Amhara Region, Ethiopia, 2017.
16. Gizaw B, Gebremedhin S. Factors associated with low birthweight in North Shewa zone, Central Ethiopia: case-control study. Ital J Pediatr. 2018 Jul 4;44(1):76. doi: 10.1186/s13052-018-0516-7. PMID: 29973240; PMCID: PMC6030760.
17. Demelash H, Motbainor A, Nigatu D, Gashaw K, Melese A. Risk factors for low birth weight in Bale zone hospitals, South-East Ethiopia : a case-control study. BMC Pregnancy Childbirth. 2015 Oct 13;15:264. doi: 10.1186/s12884-015-0677-y. PMID: 26463177; PMCID: PMC4604703.
18. Siyoum M, Melese T. Factors associated with low birth weight among babies born at Hawassa University Comprehensive Specialized Hospital, Hawassa, Ethiopia. Ital J Pediatr. 2019 Apr 11;45(1):48. doi: 10.1186/s13052-019-0637-7. PMID: 30975170; PMCID: PMC6460807.
19. Mengesha HG, Wuneh AD, Weldearegawi B, Selvakumar DL. Low birth weight and macrosomia in Tigray, Northern Ethiopia: who are the mothers at risk? BMC Pediatr. 2017 Jun 12;17(1):144. doi: 10.1186/s12887-017-0901-1. PMID: 28606178; PMCID: PMC5469141.
20. Tela FG, Bezabih AM, Adhanu AK, Tekola KB. Fetal macrosomia and its associated factors among singleton live-births in private clinics in Mekelle city, Tigray, Ethiopia. BMC Pregnancy Childbirth. 2019 Jul 1;19(1):219. doi: 10.1186/s12884-019-2379-3. Erratum in: BMC Pregnancy Childbirth. 2019 Dec 24;19(1):521. PMID: 31262264; PMCID: PMC6604312.
21. Biratu AK, Wakgari N, Jikamo B. Magnitude of fetal macrosomia and its associated factors at public health institutions of Hawassa city, southern Ethiopia. BMC Res Notes. 2018 Dec 13;11(1):888. doi: 10.1186/s13104-018-4005-2. PMID: 30545390; PMCID: PMC6293502.
22. Wondie T, Jara D, Ayana M. Factors Associated with Macrosomia among Neonates Delivered at Debre Markos Referral Hospital, Northwest Ethiopia, 2014: A Case Control Study. J Diabetes Metab. 2014; 5(468): 2.
23. Snijders TA, Bosker RJ. An introduction to basic and advanced multilevel modeling. Sage, London.  1999.
24. Goldstein H. Multilevel statistical models (Vol. 922). John Wiley & Sons. 2011.
25. Agresti A. An introduction to categorical data analysis, John Wiley & Sons. Inc., Publication. 1996.
26. Demographic E. Health survey: Addis Ababa. Ethiopia and Calverton, Maryland, USA: central statistics agency and ORC macro, 2011.
27. Agbozo F, Abubakari A, Der J, Jahn A. Prevalence of low birth weight, macrosomia and stillbirth and their relationship to associated maternal risk factors in Hohoe Municipality, Ghana. Midwifery. 2016 Sep;40:200-6. doi: 10.1016/j.midw.2016.06.016. Epub 2016 Jun 25. PMID: 27474932.
28. Manyeh AK, Kukula V, Odonkor G, Ekey RA, Adjei A, Narh-Bana S, Gyapong M. Socioeconomic and demographic determinants of birth weight in southern rural Ghana: evidence from Dodowa Health and Demographic Surveillance System. BMC pregnancy and childbirth. 16(1): 160.
29. Jawarkar AK, Lokare PO, Dore S. Study of socio-demographic and maternal determinants influencing birth-weight. J MGIMS. 2012; 17(2): 28-33.
30. Gu S, An X, Fang L, Zhang X, Zhang C, Wang J, Liu Q, Zhang Y, Wei Y, Hu Z, Chen F, Shen H. Risk factors and long-term health consequences of macrosomia: a prospective study in Jiangsu Province, China. J Biomed Res. 2012 Jul;26(4):235-40. doi: 10.7555/JBR.26.20120037. Epub 2012 Jul 6. PMID: 23554754; PMCID: PMC3596738.
31. Abubakari A, Kynast-Wolf G, Jahn A. Maternal Determinants of Birth Weight in Northern Ghana. PLoS One. 2015 Aug 17;10(8):e0135641. doi: 10.1371/journal.pone.0135641. PMID: 26281013; PMCID: PMC4539219.
32. Amini P, Moghimbeigi A, Zayeri F, Mahjub H, Maroufizadeh S, Omani-Samani R. Evaluating The Impact of Risk Factors on Birth Weight and Gestational Age: A Multilevel Joint Modeling Approach. Int J Fertil Steril. 2018 Jul;12(2):106-113. doi: 10.22074/ijfs.2018.5330. Epub 2018 Mar 18. PMID: 29707925; PMCID: PMC5936606.
33. AbdalQader MA, Shah SA, Isa ZM, Ghazi H., Badilla I, Hasan TN. Factors related to low birth weight babies in Baghdad city, Iraq. Malaysian J Public Heal  Med. 2014; 14(2): 45-9.
34. Dahlui M, Azahar N, Oche OM, Aziz NA. Risk factors for low birth weight in Nigeria: evidence from the 2013 Nigeria Demographic and Health Survey. Glob Health Action. 2016 Jan 19;9:28822. doi: 10.3402/gha.v9.28822. PMID: 26790460; PMCID: PMC4720686.
35. Muula AS, Siziya S, Rudatsikira E. Parity and maternal education are associated with low birth weight in Malawi. Afr Health Sci. 2011 Mar;11(1):65-71. PMID: 21572859; PMCID: PMC3092318.
36. Akindele RN, Audu LI, Mokuolu OA. Macrosomic births in abuja: A case-control study of predisposing factors and early neonatal outcome. Niger J Clin Pract. 2017 Mar;20(3):320-327. doi: 10.4103/1119-3077.196060. PMID: 28256487.
37. Belsley DA, Kuh E, Welsch RE. Regression diagnostics: Identifying influential data and sources of collinearity (Vol. 571). John Wiley & Sons. 2005.
38. Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American statistical Association. 1993; 88(421): 9-25.
39. Chen S, Yang Y, Qu Y, Zou Y, Zhu H, Yang H, Liu C. Both maternal and paternal risk factors for term singleton low birthweight infants in rural Chinese population: a population-based, retrospective cohort study. Scientific reports. 2018; 8(1): 1-7.
40. Cruz J, Grandía R, Padilla L, Rodríguez S, Hernández García P, Lang Prieto J, Márquez-Guillén A. Macrosomia Predictors in Infants Born to Cuban Mothers with Gestational Diabetes. MEDICC Rev. 2015 Jul;17(3):27-32. doi: 10.37757/MR2015.V17.N3.6. PMID: 26947155.
41. Figueiredo ACMG, Gomes-Filho IS, Batista JET, Orrico GS, Porto ECL, Cruz Pimenta RM, Dos Santos Conceição S, Brito SM, Ramos MSX, Sena MCF, Vilasboas SWSL, Seixas da Cruz S, Pereira MG. Maternal anemia and birth weight: A prospective cohort study. PLoS One. 2019 Mar 18;14(3):e0212817. doi: 10.1371/journal.pone.0212817. PMID: 30884493; PMCID: PMC6422668.
42. Goldstein H, Rasbash J. Improved approximations for multilevel models with binary responses. Journal of the Royal Statistical Society: Series A (Statistics in Society). 19966; 159(3): 505-513.
43. Hack M, Schluchter M, Margevicius S, Andreias L, Taylor HG, Cuttler L. Trajectory and correlates of growth of extremely-low-birth-weight adolescents. Pediatr Res. 2014 Feb;75(2):358-66. doi: 10.1038/pr.2013.209. Epub 2013 Nov 11. PMID: 24216539; PMCID: PMC3992255.
44. Hosmer DW, Lemeshow S, Sturdivant RX. Applied logistic regression. John Wiley & Sons. 2011. 398.
45. Hosmer DW, Lemeshow S. Applied Logistic Regression. John Wiley & Sons. New York. 2000.
46. Hosmer DW, Hosmer T, Le Cessie S, Lemeshow S. A comparison of goodness‐of‐fit tests for the logistic regression model. Statistics in medicine. 1997. 16(9): 965-980.
47. Idowu JMV, Opeyemi AO, Samuel BZO, Ayobami A.. Determinants of Birth Weight in South western Nigeria. The Journal of Medical Research. 2019; 5(2): 79-83.
48. Kayode-Adedeji, B., Egharevba, O., & Omoregbee, H. (2018). Prevalence of HBW  and neonatal complications in a Nigerian suburban hospital: a five year study. Journal of Pediatric and Neonatal Individualized Medicine (JPNIM), 7(1), e070120.
49. Laird NM. Empirical Bayes methods for two-way contingency tables. Biometrika. 1978; 65(3); 581-590.
50. Mai AH, Abbassia D. The prevalence of fetal macrosomia at the specialized hospital of gynecology and obstetrics of Sidi Bel Abbes (West of Algeria). Journal of Nutrition & Food Sciences. 2014; 4(3): 1.
51. Menard S. Applied logistic regression analysis. Sage. 2016.
52. Noor N, Kural M, Joshi T, Pandit D, Patil A. Study of maternal determinants influencing birth weight of newborn. Archives of Medicine and Health Sciences. 2015; 3(2): 239.
53. Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. Sage. 2002; 1.
54. Ryan T. Modern Regression Methods 474 John Wiley & Sons. Inc. New York. 1997.
55. Stiratelli R, Laird N, Ware JH. Random-effects models for serial observations with binary response. Biometrics. 1984 Dec;40(4):961-71. PMID: 6534418.
56. Wong Gy, Mason Y. The Hierarchical Logistic Regression. Model for Multilevel Analysis, Journal of the American Statistical Association.  1985. 80(5): 13-524.
57. Yao ING, Bohoussou PEK, Menin MM, Gianola G, Bazan E. Macrosomia at the Center Hospital of Montelimar (France): 141 Cases Report. Open Journal of Obstetrics and Gynecology. 2017; 7(9): 966-972.