Global Journal of Ecology
Search for the dispatch schedule optimal configuration for managing releases of the complex “Lake Baikal - Irkutsk Reservoir”
Alexander Leonidovich Buber * and Vladimir Buber
Cite this as
Buber AL, Buber V (2022) Search for the dispatch schedule optimal configuration for managing releases of the complex “Lake Baikal - Irkutsk Reservoir”. Glob J Ecol 7(1): 013-020. DOI: 10.17352/gje.000054Copyright
© 2022 Buber AL, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.The article considers methods for constructing optimal (in the Pareto sense) coordinates of the dispatch schedules for managing releases for the water management complex “Lake Baikal - Irkutsk Reservoir”. Statistical reliability criteria such as the number and depth of violations are used as optimization criteria. The construction of the optimal dispatch schedule is carried out based on water resource calculations for long-term hydrological inflow series from 1903 to 2016 (the number of the periods per year is 24) and modern hierarchically ordered requirements of water users. Since the water users’ requirements, as a rule, conflict with each other, a multi-criteria analysis of various optimal dispatch schedules were used to find the optimal Trade-off solution. To search for the optimal configuration of the dispatcher, the author’s methods of local optimization were developed, which allow solving a complex non-linear programming task in a reasonable time. Software for water resource calculation and optimization was developed with the VBA language in the Excel environment.
Introduction
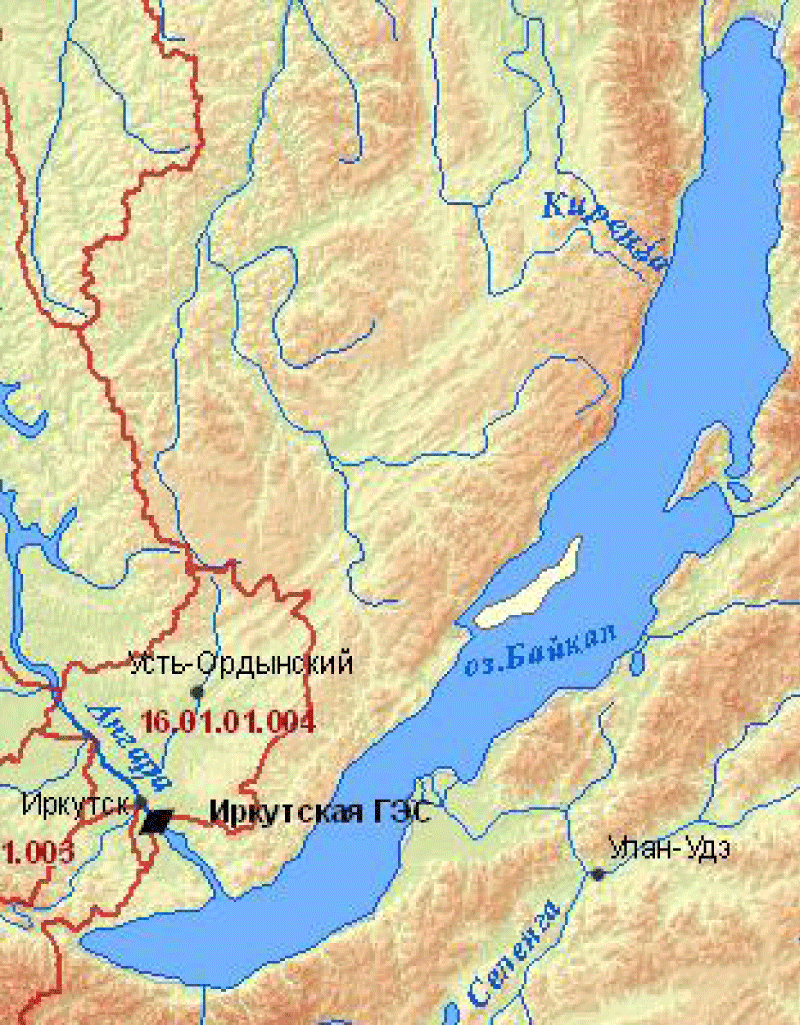
The Irkutsk hydroelectric complex is the first stage of the cascade on the Angara river. The cascade, in addition to the Irkutsk HPP, also includes the Bratsk, Ust-Ilimsk, and Boguchanskaya HPPs. The dam of the Irkutsk HPP is located at a distance of 56 km from the source of the Angara River (Figure 1). Lake Baikal is the main regulating capacity of the reservoir. After the creation of the Irkutsk hydroelectric complex, the average long-term level of the lake increased by about 0.8 m.
The Irkutsk reservoir is formed by a medium-pressure run-of-river hydroelectric complex, consisting of a hydroelectric power station, an earthen dam, and water intake facilities of the Irkutsk water pipeline. Due to the limited capacity of the Angara River source, the useful volume of Lake Baikal is limited to 31.5 km3. The value of the useful volume allows for long-term regulation of the flow. The water resources of the Irkutsk reservoir and Lake Baikal are used for the needs of energy, water transport, and fisheries, to cover the water consumption of industry and the population, and to cut off the maximum flood flow to prevent floods in the lower reaches.
The maximum and minimum levels of Lake Baikal are limited by the requirements for the conservation and sustainable functioning of the lake’s ecosystem and the adjacent territory and are 456 m and 457 m respectively Figure 1.
The presented scientific developments are based on the classical method of water management and water-energy calculations and the simulation method. Excel spreadsheets with integrated VBA language are used as a tool. Water management calculations are performed based on long-term observed hydrological series using Dispatch Schedules of various configurations. The statement of the problem and the mathematical model are made by the Guidelines for the development of rules for the use of water resources in reservoirs [1].
The engineering statement of main task of the research is to select a flow control regime that provides a given range of fluctuations in the level of Lake Baikal, as well as a set of water management and water-energy indicators of HPPs. In the process of calculations using the developed computer technology, the releases at the hydroelectric complex are determined, by the rules for regulating the flow, according to the relevant dispatch schedules, the course of levels in the upstream and downstream of the Irkutsk HPP, the developed power and electricity generation.
The aim of the research was the development of computer technology and software that allows for determining the optimal configuration of the dispatch schedule depending on the historical inflow series and the conflicting requirements of water users. The simulation model is adapted to use hydrological series of arbitrary duration with 24 settlement intervals per year, a given number of dispatch schedule zones for each settlement interval, and an arbitrary number of reliability criteria. The power of the developed computing technology is limited only by the computing capabilities of Excel.
To analyze the results of modeling experiments in the VBA language, special software has been developed that makes it possible to estimate the number and depth of interval and annual violations of requirements, to control the availability and reliability of meeting industry water consumption. The used technology allows for an arbitrary number of criteria, each of them is set depending on the system control parameters: the volume and level of water in the Lake Baikal releases the downstream of the Irkutsk hydroelectric complex, levels in the basins of the Irkutsk hydroelectric complex and electricity generation of the HPP.
As a result of the research, a mathematical model, algorithms, and software have been developed to search for the optimal configuration of the dispatch schedule for controlling releases downstream of the Irkutsk HPP. The quality of control according to the dispatch schedule was determined based on a statistical analysis of the results of water management calculations in terms of the number and depth of violations.
The developed software and various combinations of optimization algorithms were used in the search for optimal dispatch schedule (DS) configurations in the interests of various water users: utilities, transport, ecology, fisheries, and flood prevention. The current dispatcher schedule of 1988 was used as the base one.
As mentioned above, the research is based on the use of water balance equations similar to the work [2].
The article [2] deals with the management of reservoir networks in conditions of economic, social, and environmental constraints. Hydropower is the most environmentally friendly way of generating electricity. Hydroelectric power plants do not emit any standard pollutants into the atmosphere. However, it is not free from economic, social, and environmental problems. The main ones are the impact of reservoirs on the flora and fauna of adjacent areas, flood risks, and problems with navigation and water supply. The paper considers the problem of finding the optimal operating modes of reservoirs from the point of view of control theory and operations research. It was emphasized that the solution to a multicriteria problem often consists in reducing it to a set of single-criteria optimal control problems. As a result of solving these problems, a set of Pareto optimal solutions is obtained, which form the Pareto frontier. The choice of operating mode must then be made by decision-makers on the base of negotiations.
In [3] several modeling approaches are presented: based on DS and based on optimization. It is argued that there is no single generally accepted model of river basin management widely used by practitioners. It is shown that there is an effective way to develop and interpret solutions obtained based on optimization to correct the existing Dispatch Rules for the operation of the reservoir when operating in real-time on a short time horizon. In this case, DS management is performed based on a combination of revised operating rules and a short-term flow forecast. The potential value of this approach is illustrated by the example of India, where most river basin planning and management models are based on DS.
Materials and methods
In Russia, reservoir release rules are based on the Dispatch schedule (DS). Regulatory documents that define the procedure for regulating reservoirs with the help of DS [1] and provide criteria for assessing the quality of DS have been developed.
DS is the set of the rules for the reservoir flow regulation, allowing to determine the reservoir discharges within the given year intervals, depending on the reservoir water level (volume) and time period. The dispatcher consists of the set of nodal points that are specified at each interval boundary of the year. For each zone between two adjacent nodal points at the same interval boundary, the range of permissible water flow discharge rates is set. The points form piecewise linear curves (interrupt lines) ordered by levels.
Control with DS using is carried out according to the following rules: releases from the reservoir are assigned based on the calculated value of the water level in the reservoir at the end of the control interval so that the average values of water discharges over the interval were equal to the corresponding values of that dispatcher schedule zone, within which the calculated water level will be at the end of the control interval [1].
The main indicator of reliability is the probability of providing the consumer with water. The reliability is determined based on statistical processing of water resource calculation results performed for long-term series of observed inflows. The reliability is calculated by the Equation 1 [1].
P= 100·M/(N+1) (1)
Where M is the number of calculation periods in which the water user requirements were not violated, and N is the total number of calculation periods in the long-term hydrological series.
When developing release rules, it is necessary to determine such a configuration of the dispatching schedule, which will provide each water user with the following standard reliability according to Table 1.
In this work, an attempt to improve the quality of water resources management according to dispatch schedules in the case of the lake Baikal-Irkutsk reservoir complex management is presented.
The quality of the designed dispatch schedule of the lake Baikal-Irkutsk reservoir complex was determined based on the water resource management calculations for a long-term hydrological inflow series using water balance according to Equation 2.
Wend = Wbeg+Q-R (2)
Where
Wbeg, Wend - reservoir volumes at the beginning and the end of time interval respectively
Q – interval inflow volume
R - interval reservoir discharge volume
The bathymetric function shown in Equation 3 was used to calculate reservoir levels based on known volume values, where H is reservoir level.
H = f(W) (3)
As a result, the number of violation years was calculated for each water user mentioned in the previous report. The violation year is the year with at least one deviation from the water users’ requirements.
As a rule, it is impossible to fulfill all users’ requirements simultaneously. Thus, a conflict of interest arises, and it is necessary to build one or more compromise dispatch schedules agreed with water users. To build a compromise dispatch schedule it is possible to operate as follows.
Suppose there are a number of water users’ requirements that must be satisfied in the management process. Let this number be equal to K.
Let Vk be the number of violation years for the kth requirement.
Let Pk be the penalty coefficient that determines the place of k-th requirement in the priorities of water users’ requirements hierarchy. The larger P-value the more significant is the requirement.
Then the penalty objective function Fk for k-th requirement violation can be defined as shown in Equation 4.
Fk = Vk×Pk (4)
The total (for all requirements) penalty objective function F then maybe the sum of Fk. presented in Equation 5.
The F value can serve as an assessment of dispatching management quality.
The lower value of F, the higher the quality of the dispatcher for the used penalty coefficients set.
Thus, the problem can be formulated as follows - to find the dispatcher nodal points configuration for which object function has a minimum F=Fmin for the given set of penalty coefficients.
Dispatcher optimization can be performed by searching for new positions of dispatcher nodal points on the boundaries of intervals.
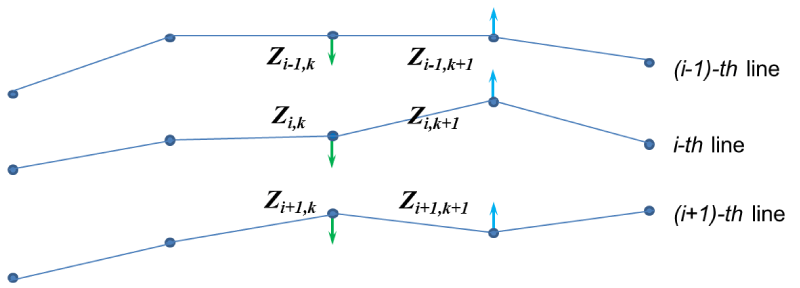
The nodal point on the ith line and the k-th interval can be shifted upward to the (i-1)-th line direction or downward to the (i+1)-th dispatcher line direction (Figure 2).
For upward shifting new point coordinate can be calculated as a linear combination of Zi−1, and Zi,k coordinates according to Equation 6.
For downward shifting - as a linear combination of Zi, and Zi+1,k coordinates as shown in Equation 7.
In both cases, shifting parameter 𝛼 takes values between 0 and 1. If zero, then there is no displacement, if 1, then there is a complete displacement to the adjacent point up or down, respectively Figure 2.
The Golden Ratio method was used to find the values 𝛼* and 𝛼** that minimize F* when the nodal point of the dispatcher is shifting upward and F** when the nodal point is shifting downward respectively.
Among the 𝛼* and 𝛼** values, that one is selected for which the value of F is less. It defines a new nodal point position Zi,k which minimizes the objective function value.
Two types of dispatcher optimization algorithms were used.
The first one is the “vertical” or V algorithm, the second one is the “horizontal” or H algorithm.
When “Vertical” - calculations of the nodal point’s optimal positions are performed sequentially for all ‘intervals boundaries – at each border simultaneously for all lines. Thus, the nodal points for two adjacent interval boundaries can be shifted in different directions. The self-similarity of the dispatcher’s lines maybe not be preserved (Figure 3).
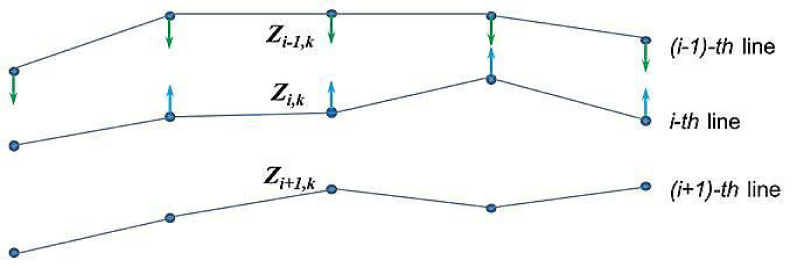
When “Horizontal” - calculations of the nodal points’ optimal positions are performed sequentially for all lines – at each line simultaneously for all points. All nodal points of the same line are shifting in the same direction. Some kind of self-similarity of the dispatcher’s lines is preserved (Figure 4).
In both cases, the nodal point coordinates of the first (upper) and the last (lower) lines remain unchanged. These lines hold their positions.
The combined optimization algorithm involves the alternate use of vertical and horizontal algorithms. Both can be applied an ‘arbitrary number of times in an ‘arbitrary order. In this case, the results of the calculations at the previous step are transmitted as source data for the subsequent calculations.
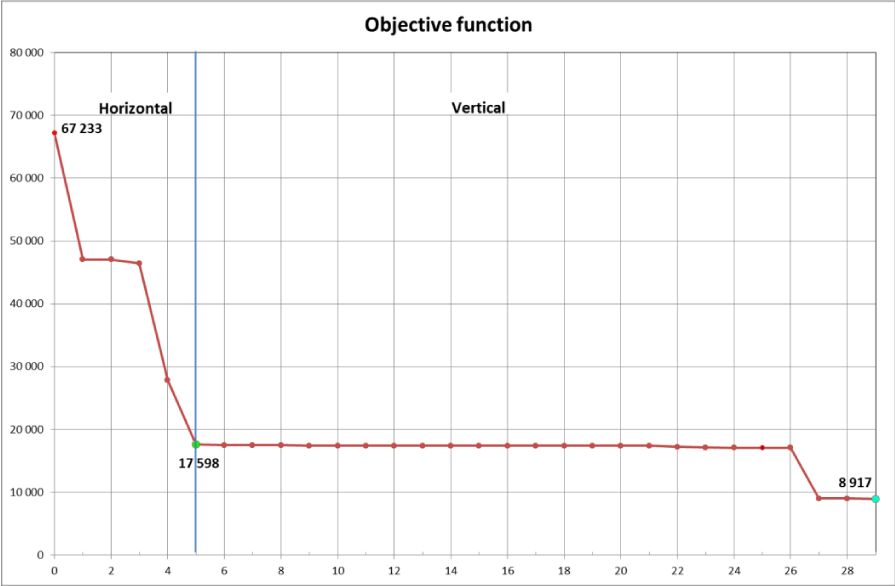
As an example, the effect of optimization on the objective function for HV is shown in Figure 5.
Results
To check the effectiveness of the proposed method for the searching of the dispatch schedule optimal coordinates, six various calculations for the current dispatch schedule (DS) 1988 were performed.
- Water resource calculation (WRC)
- Four successive horizontal optimizations (HHHH) with the current priorities of the water users’ requirements.
- A combination of four successive pairs of horizontal and vertical optimizations (HVHVHVHV) with the current priorities of the water users’ requirements.
- A combination of four successive pairs of horizontal and vertical optimizations (HVHVHVHV) with priorities in favor of environmental requirements.
- A combination of four successive pairs of horizontal and vertical optimizations (HVHVHVHV) with priorities in favor of the flood protection requirement in winter.
- A combination of four successive pairs of horizontal and vertical optimizations (HVHVHVHV) with priorities in favor of the flood protection requirement in winter and throughout the year.
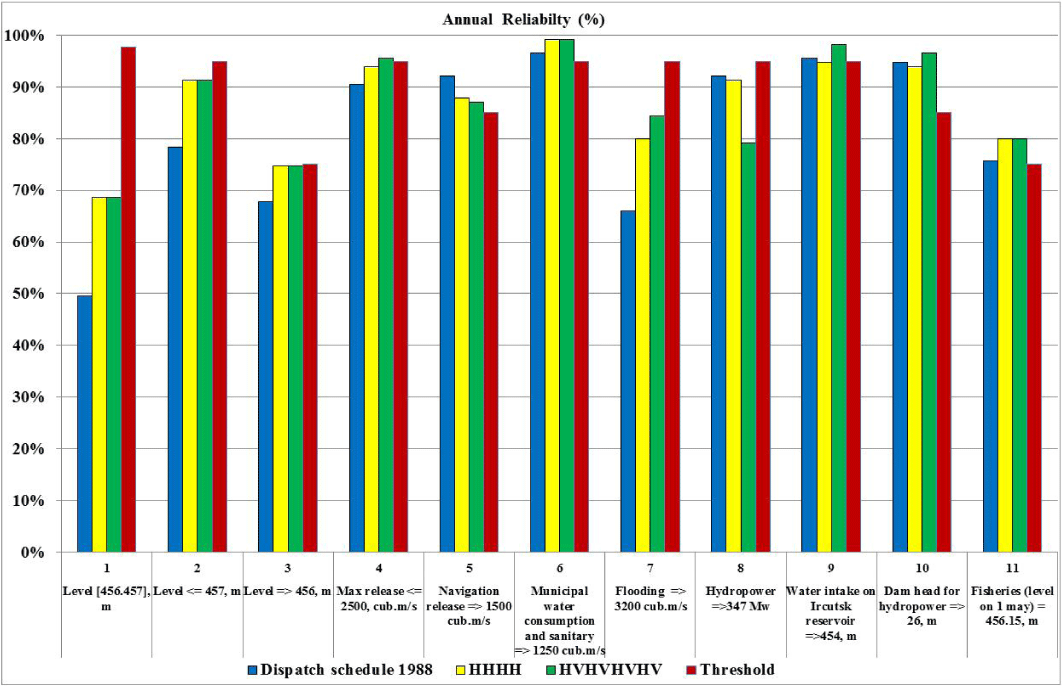
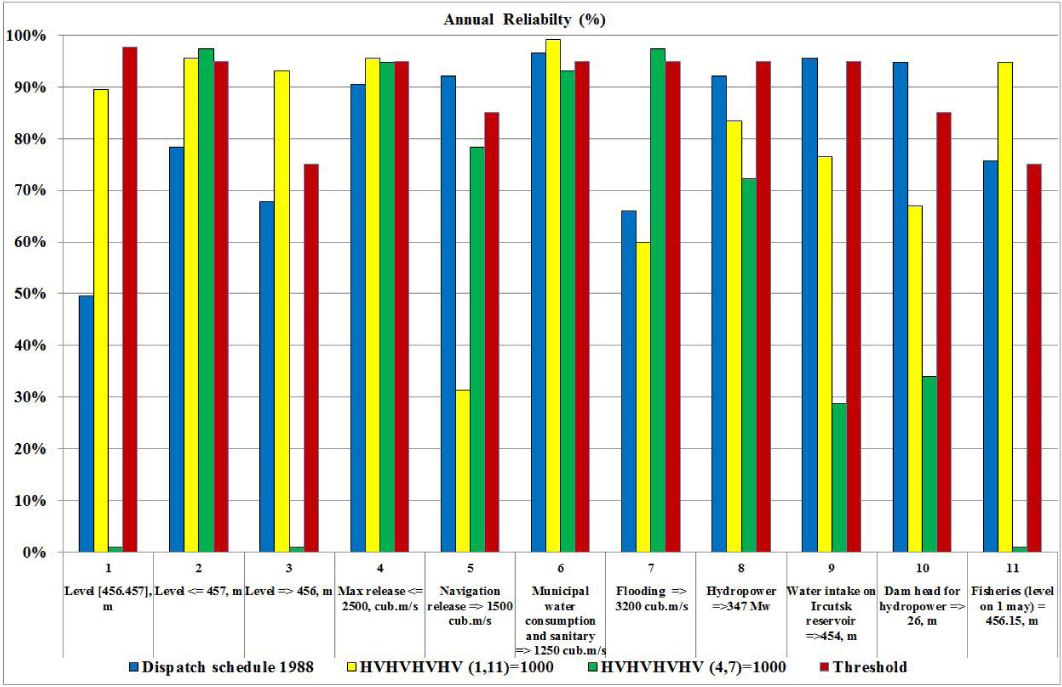
Eleven current requirements of water users (11 criteria in optimization task) were used:
- The Lake Baikal level range (456, 457) m;
- The Lake Baikal level ≥ 456 m;
- The Lake Baikal level ≤ 457 m;
- The maximum release in winter is ≤ 2500 m3/s;
- The navigation release ≥ 1500 m3/s;
- The water supply release (1250, 1300) m3/s;
- Flood control release ≤ 3200 m3/s;
- Guaranteed winter power ≥ 347 MW;
- The Irkutsk reservoir upstream level for water intakes ≥ 454 m;
- The dam pressure for HPP ≥ 26 m;
- The Lake Baikal level on May 1 for normal fish spawning = 456.15 m.
The following priorities of water users have been adopted as shown in Table 2.
A period of 114-years of Hydrological Inflow Series (1903-2016) was used in the calculations. Each year is divided into 24 time periods (decade or month).
The result of calculations for each option is reliability by criteria. Table 3 shows the reliability for each calculation option, threshold reliability for normal water consumption by the number of non-violation years, and the original set of penalties that determine the adopted hierarchy of priorities for eleven criteria.
Figure 6 shows a diagram comparing the security under the current DC 1988 with various optimization options. The diagram clearly shows that after optimization, reliability indicators for criteria 1-4, and 7 have significantly improved, and the indicator for criterion 8 has deteriorated. The remaining reliability indicators have not changed much. Unfortunately, even optimization does not allow us to satisfy environmental requirements according to criterion 1 and flood control requirements according to criterion 7.
Figure 7 shows a comparison diagram of reliability according to the current DS 1988 with optimization options in favor of ecology and favor of flood control criteria. The diagram clearly shows that if the preference is given to environmental requirements and neglect of other criteria, then it is possible to significantly improve the reliability indicators in ecology (criteria 1, 2, 3, 11). At the same time, reliability indicators for criteria 5 (transport), 7 (flood control), and from 8 to 10 are significantly worsened. If preference is given to flood control requirements and other criteria are neglected, then it is possible to improve significantly the flood control indicators of reliability (increase them to normative), however, environmental criteria decrease strongly (criteria 1, 3, 11 are practically reduced to zero). Reliability indicators for criteria 5 and from 8 to 10 are also worsening.
Discussion
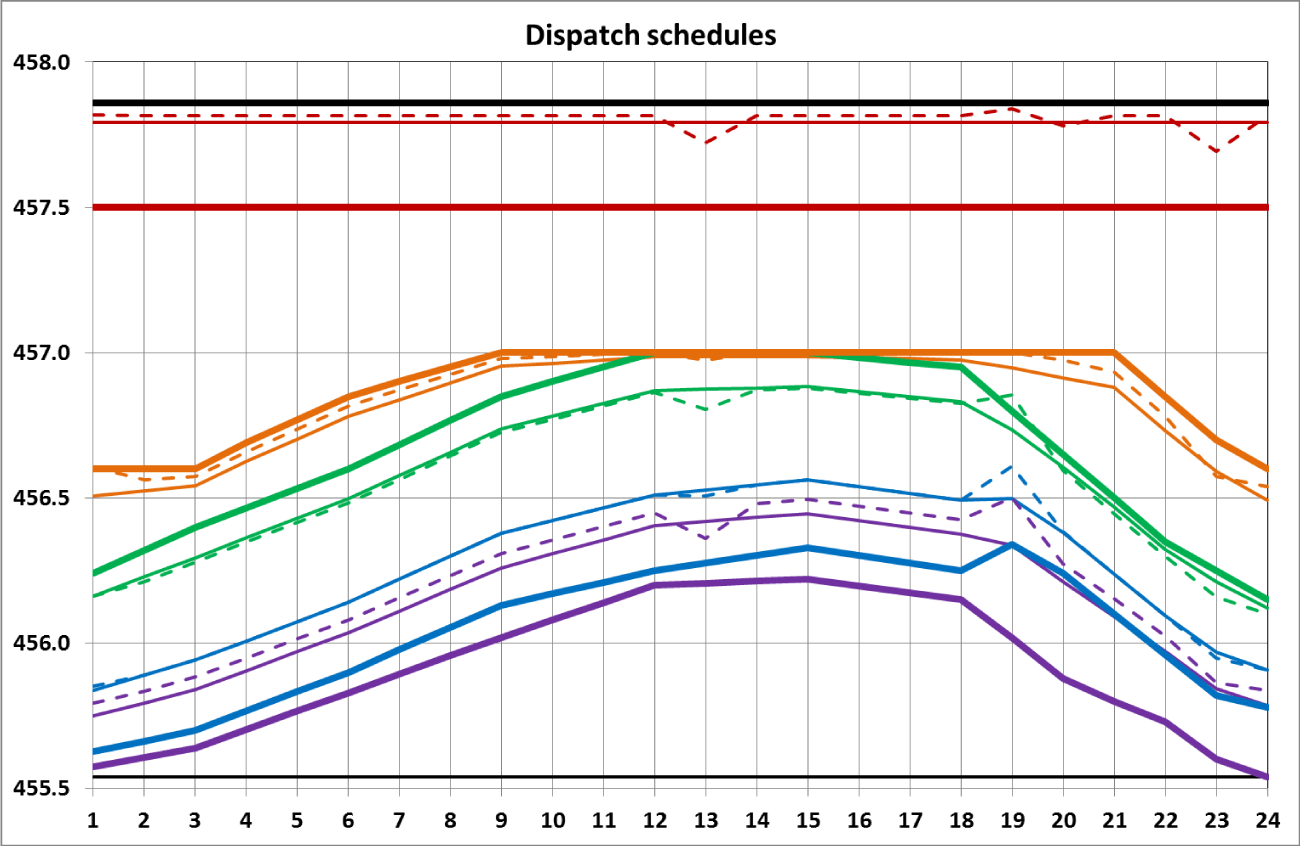
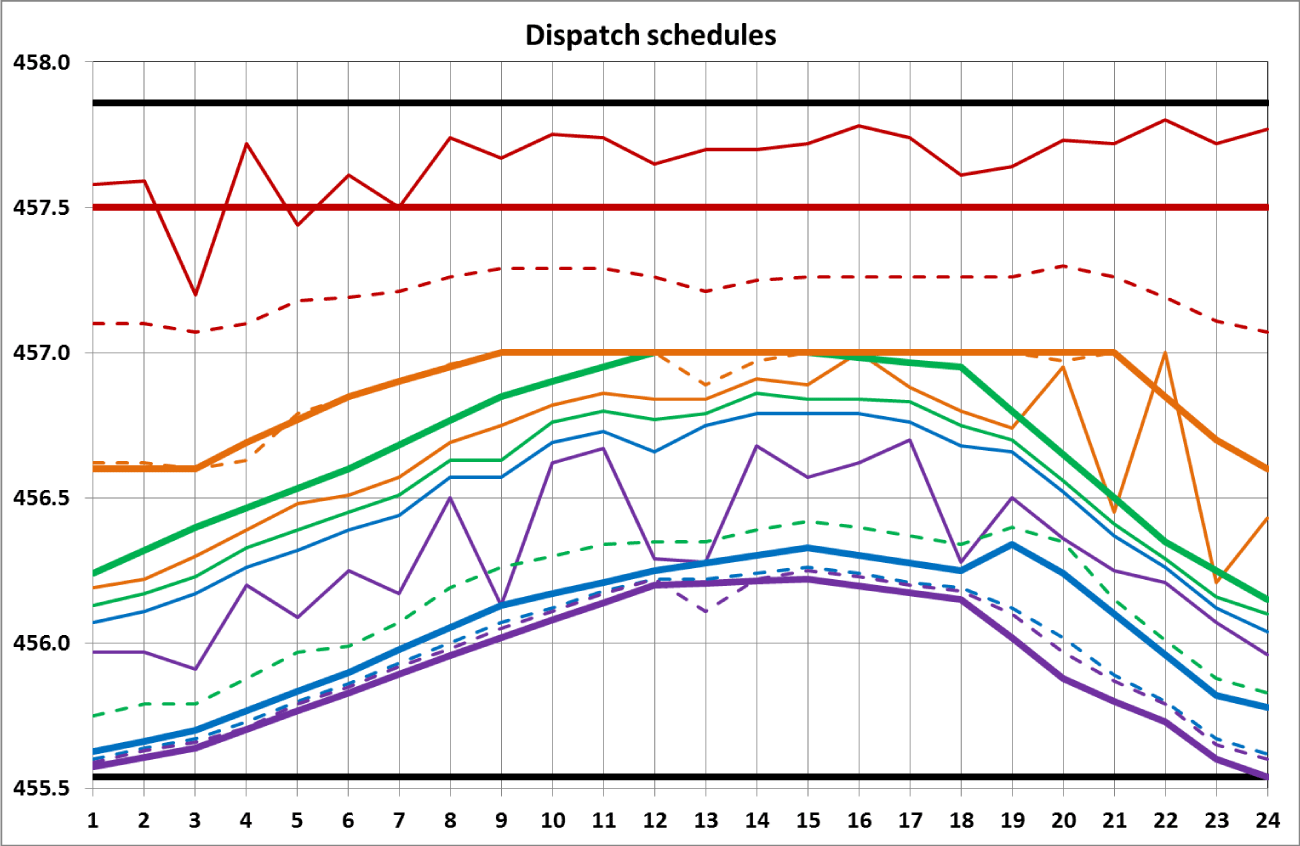
The calculations carried out show that the ecological requirement for the range of changes in Lake Baikal levels within 456 m and 457 m cannot be technically implemented. Therefore, it was necessary to change the decree of the Government of the Russian Federation No. 234 [4], which establishes the specified range, since it is impossible to fulfill it. The calculations carried out by the authors made it possible to substantiate the changes in the permissible range of fluctuations in Lake Baikal levels (455.54 m, 457.5 m) and fix them in the text of the annual temporary resolutions.
Figures 8 and 9 show a comparison of DS configurations for various calculation options.
Conclusion
The obtained results allow us to conclude that with the proposed method, it could be possible to obtain the various dispatch schedules for finding compromise solutions, taking into account the requirements of various water users in the case of water resources shortage.
Further, based on negotiations with stakeholders, using the methods of multi-criteria analysis, it is possible to choose the optimal compromise DS, including in favor of the environment, which, as a rule, is affected in regions with a lack of water resources.
- Methodological guidelines for the development of rules for the use of reservoirs (Order of the Ministry of Natural Resources of the Russian Federation of January 26, 2011.
- Castelletti A, Pianosi F, Soncini-Sessa R. Water reservoir control under economic, social and environmental constraints. Automatica. 2008; 44:1595–1607.
- Ilich N, Basistha A. Importance of multiple time step optimization in river basin planning and management: A case study of Damodar River basin in India. Hydrol Sci J. 2021; 66: 809-825,
- Decree of the Government of the Russian Federation, 26 March 2001 N 234: On the Limiting Values of the Water Level in Lake Baikal in the Implementation of Economic and Other Activities.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.


 Save to Mendeley
Save to Mendeley
