Fundamental aspects of isovolumetric contractility measurements of urinary bladder

Introduction

In 2004 Griffiths published: “Detrusor Contractility: Order Out of Chaos” [1]. It was a critical assessment of the many competing ways of assessing detrusor contractility in the urodynamic clinic. Different isovolumetric methods and pressure flow studies were considered.

In 1978 probably the first clinical contractility parameter, based on isovolumetric bladder, was introduced [2]. In that time the need for a contractility parameter was born to be able to observe damage on contractile tissue that might be caused by the clinical application of fast or stepwise cystometry to evaluate pressure relaxation and visco-elastic properties of the bladder [3]. Since the introduction of the concept of contractility many other contractility parameters and methods of determination for clinical evaluation of active bladder function have been developed. However, different fundamental aspects of contractility may contribute to the seen chaos in these clinical applications. In present consideration this is illustrated for the isovolumetric method.

Contraction is synonym for shortening of active muscular tissue. Shortening of circumference of the bladder wall is the requisite for the evacuation phase of the bladder. Rate of expulsion Q of bladder contents is determined by velocity of shortening of bladder wall. This velocity of shortening is reduced by bladder pressure, which can be built up by the resistance to flow of the urethra. The relation between velocity of shortening v and load of smooth muscle F for maximal stimulated bladder strips have been evaluated of pig bladders [4], using the normalized classic equation of Hill [5]:

(F/F0 + a/F0)(v/l+b/l) = (1+a/FO)b/l (1)

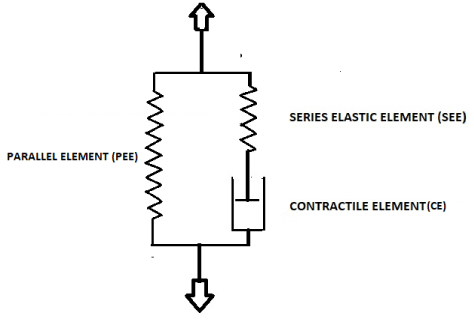
Here F is force across the strip and Fo is the isometric force, i.e. force exerted when velocity of shortening v of the stimulated strip with initial length l is reduced to zero. In this equation a and b are physiological constants. According to Hill’s equation velocity of shortening v of a stimulated strip decreases with increasing force F, following graphically a hyperbolic function. According to (1) the maximum velocity of shortening of a strip vmax /l at F = 0 is vmax /l = bFo/al. The biomechanical model of Hill’s equation is composed of two artificially separated mechanical components placed in series. One component represents distributed elasticity of bladder tissue lumped in a discrete element SEE and the other component represents distributed contractile tissue of the bladder lumped in an element CE. CE is supposed to be characterized by (1) and SEE is supposed to be characterized by a certain stress-strain relation. If we ascribe to CE a length lC and to SEE a length lE then l = lC+ lE. When a bladder strip is stimulated to contract then length of CE is shortening at a velocity v that depends on the force F generated by elongation of SEE. It is supposed that for a not stimulated strip CE is a freely movable element. Hence the series arrangement of CE and SEE cannot account for the stress-strain relation of static passive bladder tissue. Static passive stress-strain relation is represented by an extra elastic element PEE that is situated parallel to the series arrangement of CE and SEE. Hill’s mechanical model is shown in Figure 1.

Figure 1: Hill’s model [5].

Measurement of contractility based on Hill’s model

To characterize contractility of bladder tissue we look for parameters, preferably related to Hill’s equation, which can be derived from detrusor pressure p and volume V, variables which are easily recorded in a clinical setting. We consider a circumferential strip of bladder wall. Pressure p causes a force F on circumference so that F= πR2p, where R is the radius of a spherical bladder. If we ignore the contribution of the low static passive pressure, then in (1) for F/Fo we substitute F/Fo=p/po where pois the isovolumetric pressure. For velocity of shortening v we write: v/l = -(dR/dt) = -(1/4πR2)(dV/dt). For expulsion Q of the bladder holds: Q=dV/dt= -4πR2 v/l. Hence from simultaneously recording of bladder pressure p and flow Q we can derive the force-velocity relation of stimulated bladder tissue. Recording of pressure-flow relation is the base of certain category of methods for contractility measurements. For these methods we need to assume that stimulation of contractile tissue is maintained during flow at maximum level.

The original method [2] is based on determination of the relative rate of increase of pressure ((dp/dt)/p) during activation of the isovolumetric bladder, i.e. just before expulsion has started. However, isovolumetric pressure increase during stimulation of CE depends on the stress-strain relation of SEE. We relate stress S to pressure p by:

S = (3V/2Vt)p (2)

where Vt is volume of bladder tissue and is assumed to be constant. With (2) we can express for isovolumetric volume V variable (dp/dt)/p in stress:

(dp/dt)/p = (dS/dt)/S (3)

For an isovolumetric stimulated bladder the shortening of CE, -(dlC /dt) = vCE, is compensated by equal lengthening of SEE, (dlE /dt), so that: -(dlC /dt) = (dlE /dt). For known stress-strain relation of SEE we can derive velocity of shortening vCE from the increase of stress S. We need to note here that vCE is not the same as v in Hill’s equation.

Stress S generated by elasticity is commonly determined by relative elastic elongation ε = (l-l0)/l0 according to S = εE, where E is an elasticity parameter. Elastic properties of bladder tissue, studied by series of stepwise straining of tissue strips, show an exponential increase of elastic parameter E [6]. To describe this non-linear type of elasticity for large elongations it is appropriate to express strain relative to an actual reference length lo by natural strain defined by ε = ln l/lo. This natural strain is associated with a preload So which depends on chosen reference length lo. With these variables the experimentally found stress-strain relation of SEE with progressive elasticity modulus can be characterized by:

S= SOexp kε (4)

where k is a constant elastic stiffness parameter.

Then dS/dt=kS (dε/dt) =kS(dlE /dt) /lo, so that with (3) holds:

(dp/dt)/p = (dS/dt) /S = k(dlE /dt) /lo (5)

Because under isovolumetric condition (dlE/dt) = -(dlC /dt), we find by dividing these velocities by reference length l = lo as length of the actual circumference of the bladder as reference length:

k(dlE /dt) /lo = -k(dlC /dt)/l = k vCE/l= (dp/dt)/p (6)

with (6) we have related parameter vCE/l of a stimulated isovolumetric bladder to the relative rate of increase of bladder pressure (dp/dt)/p. From start of stimulation pressure rises till the level is reached for start of expulsion. This pressure recording is used to determine (dp/dt)/p along pressure increase p(t).

Gordon and Siegman found for taenia coli of length l that vmax/l roughly is a constant [7] and have taken vmax/l as a parameter for contractility. According to Hill’s equation (1) vmax/l equals velocity of shortening of the strip for F=0 only under the condition of maximum of activated state. This condition, however, is built up during rising bladder pressure. As an alternative vCEmax/l was looked for as a measure of contractility that is built up during activation of an isovolumetric bladder and related to parameter Max {(dp/dt) /p}. Theoretically for (dp/dt)>0 the value of Max {(dp/dt) /p} is infinite large for p =0. We are not interested in contractility at start of activation, but we look for Max {(dp/dt) /p} attained along the rising pressure for p>0.

In a pilot study on 11 human subjects referred to in [2] Max {(dp/dt) /p} was found in the first part of rising pressure. This maximum varied between 0.17-0.99 s-1 for bladder volume in the range of 150-650 ml. It is evident that vmax/l in Hill’s equation valid for p=0 for fully activated tissue is different to vCEmax/l that here is taken as a measure of velocity of shortening derived from Max {(dp/dt) /p} for p>0 attained at unknown level of activation. For two subjects Max {(dp/dt) /p} was determined in series of voluntarily interruption of micturition. The parameter of contractility derived from Max {(dp/dt) /p} clearly was not reproducible. Bad reproducible results of this method were particularly ascribed to variation in the characteristics of elasticity in SEE [8]. To exclude an effect of inhibition of the activation by voluntarily interruption the urethra was occluded during micturition by means of a balloon catheter, referred to as the stop test [9].

Quick release studies on stimulated pig bladder strips fixed at a low passive tension have revealed remarkable features of bladder elasticity that is represented by SEE [10]. The quick shortening needed to zero tension across a stimulated strip varied for different strips of equal initial length between 4.5-20.5% of initial length. Because of this considerable variation of elasticity it was concluded that elasticity of stimulated tissue cannot be described in terms of a discrete SEE, as was supposed in the original contractility measurements. Variation of elasticity during development of contraction has been ascribed to recruitment of cross bridges. However, no explanation has been given for the large variation of elasticity found for different strips. Another remarkable conclusion drawn from the quick release studies is that the quick shortenings needed to zero tension of a stimulated strip is independent of the attained force level at which release starts. The needed equal shortenings amount only 10% on the mean of the initial length of the strip. The quick release studies have invalidated the representation of elasticity by a SEE characterized by fixed elastic parameters, like assumed in (4) and consequently also the original isovolumetric method.

More observations have shown that the development of isovolumetric pressure during activation dp/dt is slower than assumed by Gordon and Siegman [7] and depends on different stimulation variables. It turned out that the first part of dp/dt increases almost exponentially with increasing p to a maximum and then decreases almost linearly with increasing p to maximum isovolumetric pressure p0 [11].

Despite these complications with the use of variable (dp/dt) /p to derive a parameter for contractility its use was re-introduced in 2017 by Fry, et al. [12] as a new parameter to determine bladder contractility. The authors even concluded that their method is preferable to other contractility parameters which were introduced since 1978 in clinical practice, like the watts factor and other methods evaluated by Griffiths [1].

Fry, et al. used the isovolumetric increase of detrusor pressure p of a voluntary bladder contraction before micturition to generate a plot of (dp/dt) /p versus p. Extrapolation of this plot according to a fitted hyperbolic function to the y-axis (p=0) and to the x-axis (vCE=0) is used as contractility parameter vCEmax and maximum isovolumetric pressure po respectively. Without foundation of their interpretation, the obtained fitted plot of (dp/dt) /p versus p is taken to be similar with velocity-force relation according to (1)[13]. The course of increasing pressure between 20%-80% of maximum of recorded detrusor pressure is used to fit the hyperbolic function needed for extrapolation. This maximum pressure is equal to opening pressure of urethra. Duration t20-t80 needed for the rise of pressure from 20%-80% of maximum is used for practical reasons as a contractility index DCP.

In a letter to editor Schaefer has given critical comments to this method [14] and has emphasized the clinical significance to relate detrusor strength to outflow. Here we criticize their method by referring to the fundamental problems discussed in relation the original similar method [2].

As has been explained before, the maximum of vCE derived from (dp/dt) /p by backwards extrapolation to p=0, is not equal to vmax in Hill’s equation (1). Because vmax depends on circumference l of the bladder, hence on V, it is expected that vCEmax also depends on V, which is pretended to be not the case. Hill’s equation is based on a maintained fully stimulated state. The considered isovolumetric pressure increase, however, concerns the process of development of the stimulated level of pressure. DCP and fitted extrapolated hyperbolic function is based on the measured maximum isovolumetric pressure that is reached before opening of the urethra. Maximum isovolumetric pressure po in Hill’s equation, however, is always higher than the opening pressure of urethra. Hence DCP depends on the opening pressure of the urethra, not on maximum isovolumetric pressure p0 of the bladder. To find po it would have been better to block the urethra before micturition. Backwards extrapolation to p=0 according to the fitted hyperbolic function of (dp/dt) /p derived from p between 20-80% of opening pressure of the urethra yields no right estimation of vCEmax. It is evident that the interpretation of DCP in terms of Hill’s equation is wrong. Most important complication is, what also is an explanation of failure of this method in 1978 [1], that pressure developed during contraction depends on the stress-strain relation of the tissue elasticity (SEE) that, however, has shown to be not a reproducible relation. We conclude that there are clinical and theoretical reasons not to recommend the method for determination of contractility as suggested by Fry, et al. [12].

Measurement of contractility based on an alternative model

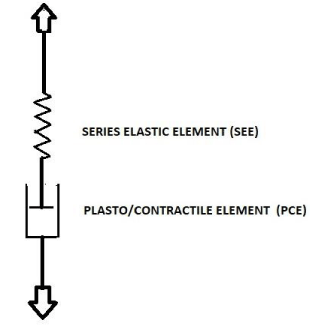
Now we come to another consideration of isovolumetric measurements. In Hill’s model the static passive properties of bladder tissue are represented by PEE. This model has been extended by elements to represent also the observed passive visco-elastic and plastic properties [4,6] of not activated bladder. Isovolumetric contractility measurements concern the transition of the bladder from passive state to fully activated state. In 1985 van Duyl published a model to describe both the passive and the active state of a bladder [15,16]. This model was particularly used to account for the observed distributed pattens of spontaneous activity which positioned a bladder at a bladder performance scale between the two extreme states of fully passive and fully active. This model would apply also to describe the transition of bladder state when it is activated. In Figure 2 this model is shown as it recently was used to describe the autonomous expulsion of the bladder by the combination of elasticity and spontaneous contraction activity [17]. In this model contractile element CE of Hill’s model has been replaced by a plasto/contractile element PCE. In contrast to element CE element PCE is not freely movable when tissue is not activated but resists to elongation by the property of plasticity of bladder tissue. The plastic elongated state of PCE is reduced by active contraction. In this model there is no need for a PEE to account for static pressure. In van Duyl’s model SEE represents all elasticity, inclusive the complicated not-reproducible elastic features found for activated tissue. The separated elements PCE and SEE correspond to virtually separated parts of bladder volume V. Element SEE corresponds to the elastic volume VE as that part of total volume V that needs to be withdrawn stepwise out of the bladder to attain zero pressure. The remaining part is rest volume VR which corresponds to the length of element PCE. Stimulated or spontaneously generated contractions reduce VR by shortening of PCE. As far during contraction activity the shortening of PCE is compensated by elongation of SEE, contraction activity is accompanied by change in pressure and change in elastic volume VE. Restauration of the contracted state of PCE is attained by bladder pressure via a process of passive relaxation till the threshold for further plastic elongation has been reached [15,16].

Figure 2:Van Duyl’s model [16].

The relation between elastic volume VE and pressure p is expressed by elastic compliance parameter CE : CE= (dVE/dp) [17]. This type of compliance differs from ICS-standard and from compliance that commonly is derived from a cystometrogram. In a study on not-stimulated pig bladders in vitro it was found that elastic volume VE, as part of different values of total volume V, and CE varies considerably [17]. For an accommodated bladder with volume between 100 and 300 ml the percentage that is ascribed to elastic volume varies in the range of 10-50% of total volume.

We referred above to the observation of large variation of elastic length for stimulated pig bladder strips of 4.5-20.5% of initial length [6]. When we translate this variation to variation of elastic volume VE of the activated bladder then we find a variation of approximately 13-50% of actual volume. This range of variation of elastic volume of a stimulated pig bladder is almost equal to the range of variation of elastic volume found for not stimulated bladder filled up to 300 ml. Further, in contrast to a not-stimulated bladder, the quick release studies have revealed that the elastic volume would be independent of the attained level of contractile state during stimulation. Hence from start to end of stimulation of an isovolumetric bladder the elastic volume would not change and hence seems to be equal to the elastic volume of the bladder in the passive state just before its stimulation. In other words during the isovolumetric increase of pressure of a stimulated bladder elastic volume and rest volume would not change and previous passive state is maintained. In this way the state of fully passive bladder, the state with spontaneous contraction and the state of fully activated bladder are functionally connected, as supposed by the model of Figure 2. This means that the pressure increase during activation can be ascribed to gradual decrease of elastic compliance CE [17]. Here we note that, though distributed patterns of localized (micro-) motions have been observed, no distributed localized shortenings of contractile tissue have been observed during isometric stimulated contractions which can be lumped in a net shortening of a discrete element (P)CE. Hence the conclusion that during stimulated isovolumetric contraction there is no change of elastic volume, sofar has not been falsified by observations of distributed contractions. This leads to the final statement that any method of evaluation of a parameter of contractility based on velocity of shortening v, as a parameter in Hill’s equation, derived from isovolumetric pressure recording is unreliable.

We try to benefit from the remarkable property of constant elastic volume during isovolumetric pressure increase during activation to characterize clinically the contractile state of the bladder. If CE is constant then Q= dV/dt= CEdp/dt. If we assume that at start of micturition CE has reached a minimum value during isovolumetric activation up to attained opening pressure of urethra and that this value of CE is constant for a small initial period, then we can derive this Min {CE} from initial flow Q(0) and initial dp(0)/dt by using equation: Min {CE}= (dV(0)/dt)/(dp(0)/dt). However, because of the observed, though still unexplained, large variation in elastic volume for passive and activated bladder we expect that parameter Min {CE} will also vary. Forced stops of flow during a micturition offer more opportunities to determine actual values of elastic compliance CE of a certain bladder. This proposed parameter Min {CE} and method of determination has not yet been clinically evaluated.

Conclusion

Although we may have contributed extra chaos in the many published methods of contractility measurements by referring to fundamental aspects of isovolumetric methods, the considered basic properties finally suggest an alternative clinical feasible method to evaluate actual contractilit y of the bladder.

1. Griffiths DJ (2004) Detrusor contractility: Order out of chaos. Scand J Urol Nephrol 215: 93-100. Link: https://bit.ly/3fAFZwT
2. Duyl van WA, Coolsaet BLRA, Mastrigt van R (1978) A new clinical parameter for the assessment of the contractility of the urinary bladder. Urol Int 33: 31-39. Link: https://bit.ly/2T698sc
3. Coolsaet BLRA, Duyl van WA, Mastrigt van R, Zwart van der R (1975) Urol Int 30: 16-26.
4. Griffiths DJ, Mastrigt van R, Duyl van WA, Coolsaet BLRA (1979) Active mechanical properties of the smooth muscle of the urinary bladder. Med Biol Eng Comp 17: 281-290. Link: https://bit.ly/33ZIjZ2
5. Hill AV (1938) The heat of shortening and the dynamic constants of muscle . Proc R Soc Ser B 126: 136-195. Link: https://bit.ly/2RzRcFZ
6. van Mastrigt R, Coolsaet BL, van Duyl WA (1978) Passive properties of the urinary bladder in the collection phase. Med Biol Eng Comput 16: 471-482. Link: https://bit.ly/3bEicuT
7. Gordon AR, Siegman MJ (1971) Mechanical properties of smooth muscle; Length-tension and force-velocity relations. Am J Phys 221: 1243-1254. Link: https://bit.ly/3fMkAkz
8. Mastrigt R van, Griffiths DJ (1979) Contractility of the urinary bladder. Urologia Intenationalis 34: 410-420. Link: https://bit.ly/3fAmS5U
9. Coolsaet BLRA (1980) Stop-Test: Une détermination qualitative de la contractilité du détrusor chez les patientes qui souffrent d’une incontinence d’effort. Journal d’Urologie 86: 187-191.
10. van Mastrigt R, Tauecchio EA (1982) Series-elastic properties of strips of smooth muscle from pig urinary bladder. Med Biol Eng Comput 20: 585-594. Link: https://bit.ly/3fvnlqe
11. van Mastrigt R, Glerum JJ (1985) Electrical stimulation of smooth muscle strips from the urinary bladder of the pig. J Biomed Eng 7: 2-8. Link: https://bit.ly/3f46Q5k
12. Fry CH, Gammie A, Drake MJ,Abrams P, Kitney DG, Vahabi B (2017) Estimation of bladder contractility from intravesical pressure-volume measurements. NeuroUrl Urodyn 36: 1009-1014. Link: https://bit.ly/3eZLqWW
13. Gammie A, Kitney D, Drake M, Abrams P, Fry C (2018) The calculation and comparison of the detrusor contractility parameter and watts factor. NeurUrol Urodyn 1-8. https://bit.ly/3fvmUfA
14. Fry CH, Gammie A¸ Drake MJ, Abrams P, Kitney DG, et al. (2017) Estimation of bladder contractility from intravesical pressure-volume measuments. NeuroUrol Urodyn 1-4.
15. van Duyl WA (1985) A model for both the passive and active properties of urinary bladder tissue related to bladder function. NeuroUrol Urodyn 4: 275-283. Link: https://bit.ly/2SVTwaw
16. van Duyl WA, Coolsaet BLRA (2021) Biomechanics of urinary bladder: spontaneous contraction activity and micromotions related to accommodation. Int Urol Nephrol. Link: https://bit.ly/2RymHjx
17. van Duyl WA, Coolsaet BLRA (2021) Biomechanics of urinary bladder: slow-filling and slow-emptying cystometry and accommodation. Int Urol Nephrol. Link: https://bit.ly/2RymHjx