Annals of Mathematics and Physics
The link between s and d components of electron boson coupling constants in one band d wave Eliashberg theory for high Tc superconductors
GA Ummarino*
2National Research Nuclear University MEPhI (Moscow Engineering Physics Institute), Kashira Hwy 31, Moskva 115409, Russia
Cite this as
Ummarino GA (2023) The link between s and d components of electron boson coupling constants in one band d wave Eliashberg theory for high Tc superconductors. Ann Math Phys 6(1): 048-051. DOI: 10.17352/amp.000077Copyright Licence
© 2023 Ummarino GA. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.The phenomenology of overdoped high Tc uperconductors can be described by a one band d wave Eliashberg theory where the mechanism of superconducting coupling is mediated by antiferromagnetic spin fluctuations and whose characteristic energy Ω0 scales with Tc according to the empirical law Ω0 = 5.8 kBTc. This model presents universal characteristics that are independent of the critical temperature such as the link between the s and d components of electron boson coupling constants and the invariance of the ratio 2∆/kBTc. This situation arises from the particular structure of Eliashberg's equations which, despite being non-linear equations, present solutions with these simple properties.
Introduction
Eliashberg's theory [1] was born as a generalization of the BCS theory to explain some anomalies in the experimental data concerning lead. Subsequently, it was seen that the theory can be successfully applied to explain the experimental data of practically almost all superconducting materials [2,3], first of all low Tc phononic superconductors [4], then magnesium diboride [5,6], graphite intercalated compound CaC6 [7], iron-based superconductors [8-12]. This theory can be applied to describe particular systems such as proximized systems [13] and field effect junctions [14-16]. For what concerns the high Tc superconductors [17-21], their properties strongly depend on their oxygen content. It is possible to identify three different regimes: under, optimal and overdoping. While the discussion is still open as regards the underdoping regime, it is almost certain that the fundamental mechanism in the optimal and over regime is due to antiferromagnetic spin fluctuations, and especially in the over regime, the experimental data can be described satisfactorily by one band d - wave Eliashbeg's theory [22,23]. Detailed studies are present in the literature on cuprates and precisely on tunneling spectra that can be reproduced by using the framework of d - wave Eliashbeg's theory [24-26]. In this paper, we provide an extensive investigation of the consequences of a different symmetry of coupling in the two components of self-energy: the renormalization function Z(iωn) (s-wave symmetry) and the gap function ∆(iωn) (d-wave symmetry) and if some link exists between them. We focus here on physical quantities which can be evaluated in the imaginary axis formalism. Furthermore, it has been experimentally determined that, in cuprates, a link [27] exists between magnetic resonance energy Ω0 and critical temperature. So we will study the properties of one band d-wave Eliashbeg's theory where a fundamental role will be played by the assumption that the representative energy Ω0 of these systems is related to the critical temperature by a universal relationship [27] Ω0 = 5.8 kBTc. This assumption represents a very strong constraint in correlating the values of the two-electron boson coupling constants λd and λs. For each value, λs we will look for the value λd which exactly reproduces the Tc superconductor and we will study which relation exists between the d and s components of the electron boson coupling constant. Finally, we will see that this model has the particular property that the relationship between the gap and the critical temperature ( ) is independent of the particular value of the critical temperature.
Model
The one-band d-wave Eliashberg equations [23,30-35] are two coupled equations: one for the gap ∆(iωn,φ) and one for the renormalization functions Z(iωn,φ). These equations, in the imaginary axis representation (here ωn denote the Matsubara frequencies), when the Migdal theorem holds [29], are:
where is the Heaviside function, ωc is cut-off energy and
We assume [2,23,30-35] that the electron boson spectral function and the Coulomb pseudopotential at the lowest order contain separated s and d -wave contributions,
as well as the self-energy functions:
We put the factor inside the definition ∆d(ωn) because, experimentally, the peak of the density of the state is, usually, identified ∆d(ωn=0) while, as we will see, Zd(ωn) is always zero. The spectral functions α2Fs,d(Ω) are normalized in the way that and of course, in this model the renormalization function is pure s-wave (Z(ωn,φ) = Zs((ωn)) while the gap function is pure d-wave ( ). We consider just solutions of the Eliashberg equations in pure d -waveform because this is the indication of the experimental data. This means that the s component of the gap function is zero and this situation happens because, usually [36], ). In the more general case, in principle, the gap function has d and s components. The renormalization function has just the s component because the equation Zd (ωn) is a homogeneous integral equation with just the solution Zd (ωn) = 0 [37]. For simplicity, we also assume that the spectral functions are the difference between two Lorentzian, i.e. where , C is the normalization constant necessary to obtain , Ω0 and γ are the peak energy and half-width, respectively. The half-width is =Ω0/2. This choice of the shape of the spectral function and the fact that , is a good approximation of the true spectral function [38] connected with antiferromagnetic spin fluctuations. The same thing also happens in the case of iron pnictides [39]. In any case, even making different choices for γ the link between λd and λs) remains the same but changes (very little) the coefficients of the linear fit. The cut-off energy is meV and the maximum quasiparticle energy is ωmax = 1100 meV. In the first approximation, we put (if the component of the gap is zero the value of is irrelevant). Now we fix the critical temperature and for any value, λs we seek the value λd that exactly reproduces the initial fixed critical temperature. After, via Padè approximants [40], we calculate the low-temperature value (T = Tc/10 K) of the gap because, in presence of a strong coupling interaction, the value ∆d(ωn=0) obtained by solving the imaginary-axis Eliashberg equations can be very different from the value ∆d obtained from the real-axis Eliashberg equations [31].
Results and discussions
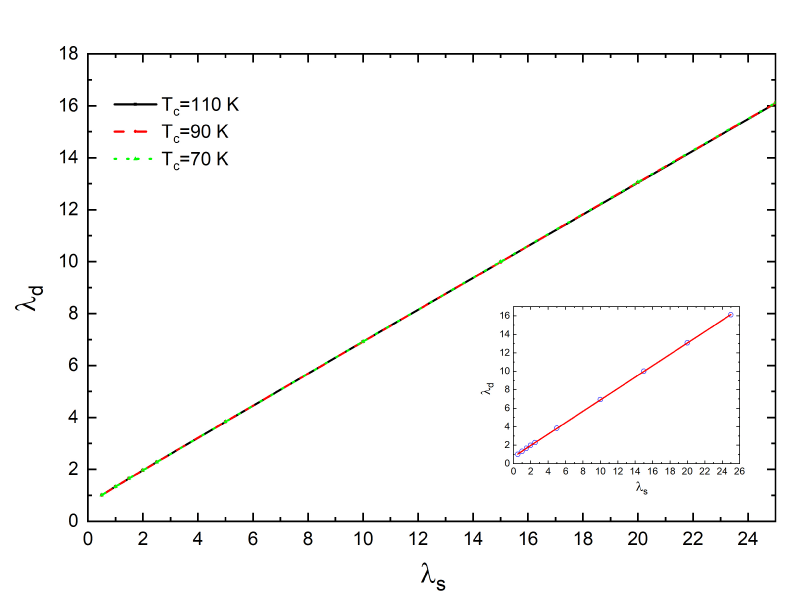
We fix three different critical temperatures (70 K, 90 K and 110 K) and for any particular critical temperature, we choose different values λs and determine which value λd exactly reproduces the chosen critical temperature by numerical solution of Eliashberg equations. In Figure 1 we can see that the three curves λd versus λs are coincident. The inset of Figure 1 it is shown the linear fit of these results. We obtain a linear link between λd and λs
These results are general and do not depend on the particular shape of the electron-boson spectral function. If we change the shape of the electron-boson spectral function and we choose, for example, we find that the linear link between λd and λs changes very little and becomes . Even the introduction of a Coulomb potential different from zero, as we have verified, does not involve a substantial modification of our results. In principle, it is possible to obtain this result (the linear link between λs and λd) in a more simple but less general way. In fact, a similar conclusion relative to the linear connection between λs and λd may also be derived from the analysis of the approximate MacMillan formula for [41] generalized to d-wave case [42]:
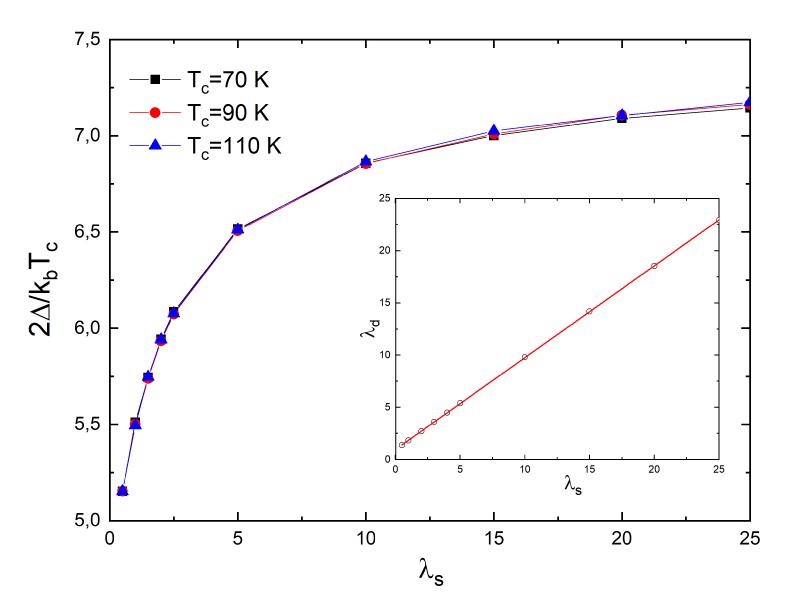
The problem is that the MacMillan equation works just in a weak coupling regime. Now we solve, for each couple of λd and λs values, the Eliashberg equations at T = Tc/10 and after, via Pade we calculate the value of superconductive gap (the energy of the density of states peak). In Figure 2 the rates are shown for three systems with different critical temperatures (70 K, 90 K and 110 K). The curves are exactly coincidental. We have also studied what happens when the ratio is equal to two as in the case of the heavy fermion [43] with Tc = 2 K which could represent an extreme situation. In this case, the link remains linear and becomes as it is possible to see in the inset of Figure 2. Finally, in the case of extremely strong coupling ( ) it is possible to demonstrate in an analytical way, following the calculus of ref 26, when , that λd ≈ λs i.e. the link remains linear.
Conclusion
In this article, it has been shown that one band d-wave Eliashbeg's theory presents universal aspects as the linear link between λd and λs or the values that are independent of the particular critical temperature. These universal aspects are related to the assumption that the typical bosonic energy is correlated to the critical temperature as shown by experimental data (Ω0= 5.8 kBTc). We here proved that in a fully numerical solution of the Eliashberg equation, such linear links hold with great accuracy. A generalization and development of our results can be obtained by explicitly considering the momentum dependence of the self-energy without average on the Fermi surface as was done by Kamila A. Szewczyk, et al. [44]. Obviously, we would include in the calculations, unlike them, as we have done now, the link, observed experimentally, between the critical temperature and the representative energy of the bosonic spectrum.
The author acknowledges support from the MEPhI Academic Excellence Project (Contract No. 02.a03.21.0005).
- Eliashberg GM. Sov Phys. JETP. 1963; 3:696.
- Ummarino GA. Eliashberg Theory. In: Emergent Phenomena in Correlated Matter, edited by E. Pavarini, E. Koch, and U. Schollwöck, Forschungszentrum Jülich GmbH and Institute for Advanced Simulations. 2013; 13.
- Marsiglio F. Eliashberg theory: A short review. Annals of Physics. 2020; 417: 168102.
- Carbotte JP. Properties of boson-exchange superconductors. Rev Mod Phys. 1990; 62: 1027.
- Daghero D, Gonnelli RS, Ummarino GA, Kazakov SM, Karpinski J, Stepanov VA, Jun J. Point-contact spectroscopy in MgB2 single crystals in magnetic field. Physica C Superconductivity. 2003; 385: 255-263.
- Daghero D, Calzolari A, Ummarino GA, Tortello M, Gonnelli RS, Stepanov VA, Tarantini C, Manfrinetti P, Lehmann E. Point-contact spectroscopy in neutron-irradiated Mg11 B2. Phys Rev B. 2006; 74: 174519.
- Sanna A, Pittalis S, Dewhurst JK, Monni M, Sharma S, Ummarino G, Massidda S, Gross EKU. Phononic self-energy effects and superconductivity in CaC6. Phys Rev B. 2012; 85: 184514.
- Torsello D, Ummarino GA, Gozzelino L, Tamegai T, Ghigo G. Comprehensive Eliashberg analysis of microwave conductivity and penetration depth of K-, Co-, and P-substituted BaFe2 As2. Phys Rev B. 2019; 99: 134518.
- Torsello D, Ummarino GA, Bekaert J, Gozzelino L, Gerbaldo R, Tanatar MA, Canfield PC, Prozorov R, Ghigo G. Tuning the Intrinsic Anisotropy with Disorder in the CaKFe4As4 Superconductor. Phys Rev Appl. 2020; 13: 064046.
- Ghigo G, Ummarino GA, L. Gozzelino, and T. Tamegai. Phys. Rev. B 96, 014501 (2017).
- Torsello D, Cho K, Joshi KR, Ghimire S, Ummarino GA, Nusran NM, Tanatar MA, Meier WR, Xu M, Budko SL, Canfield PC, Ghigo G, Prozorov R. Tuning the Intrinsic Anisotropy with Disorder in the CaKFe4As4 Superconductor. Phys Rev B . 2019;100: 094513.
- Ummarino GA. Mathematical and Physical Properties of Three-Band s± Eliashberg Theory for Iron Pnictides. Magnetochemistry. 2023;9: 28.
- Ummarino GA. Superconductive critical temperature of Pb/Ag heterostructures. Physica C. 2020; 568:1353566.
- Ummarino GA, Piatti E, Daghero D, Gonnelli RS, Sklyadneva YI, Chulkov EV, Heid R. Proximity Eliashberg theory of electrostatic field-effect doping in superconducting films. Physical Review B. 2017; 96: 064509.
- Ummarino GA, Romanin D. Theoretical Explanation of Electric Field-Induced Superconductive Critical Temperature Shifts in Indium Thin Films. Phys Status Solidi B. 2020; 2020;1900651.
- Ummarino GA, Romanin D. Proximity two bands Eliashberg theory of electrostatic field-effect doping in a superconducting film of MgB2. J Phys. Condens Matter. 2019; 31: 024001.
- Gonnelli RS, A. Calzolari, D. Daghero, L. Natale, G.A. Ummarino, V.A. Stepanov, M. Ferretti, European Physical Journal B. 2001; 22: 41.
- Alikhanzadeh-Arani S, Salavati-Niasari M, Almasi-Kashi M. Influence of the utilized precursors on the morphology and properties of YBa2Cu3O7−y superconducting nanostructures. Physica C Superconductivity. 2013; 488: 30.
- Alikhanzadeh-Arani S, Salavati-Niasari M, Almasi-Kashi M. Growth of the Dysprosium–Barium–Copper Oxide Superconductor Nanoclusters in Biopolymer Gels. Journal of Inorganic and Organometallic Polymers and Materials. 2012; 22: 1081..
- Alikhanzadeh-Arani S, Kargar M, Salavati-Niasari M. Biopolymer-protected GdBa2Cu3O7−x nanoparticles: Morphology, structure and superconducting properties. Journal of Alloys and Compounds. 2014; 614: 35.
- Kargar M, Alikhanzadeh-Arani S, Pezeshki-Nejad Z, Salavati-Niasari M. Improvement of the Superconducting Properties of Ho123 Nanoparticles via a Polymer Mediated Sol-Gel Method. Journal of Superconductivity and Novel Magnetism. 2015; 28: 13.
- Ummarino GA. Standard Behaviour of Bi2Sr2CaCu2O8+δ Overdoped. Condens Matter. 2021; 6: 13.
- Rieck CT, Fay D, Tewordt L. Energy gap, Tc and density of states in high-temperature superconductors for retarded s- and d-wave interactions. Phys Rev B. 1989; 41: 7289.
- Jiang C, Carbotte JP, Dynes RC. Boson structure in the quasiparticle density of states of superconductors with nodes in the gap. Phys Rev B. 1993; 47: 5325.
- Zasadzinski JF, Coffey L, Romano P, Yusof Z. Tunneling spectroscopy of Bi2Sr2CaCu2O8+δ: Eliashberg analysis of the spectral dip feature. Phys Rev B. 2003; 68: 180504(R).
- Ahmadi O, Coffey L, Zasadzinski JF, Miyakawa N, Ozyuzer L. Eliashberg Analysis of Tunneling Experiments: Support for the Pairing Glue Hypothesis in Cuprate Superconductors. Phys Rev Lett. 2011; 106: 167005.
- Yu G, Li Y, Motoyama EM, Greven M. A universal relationship between magnetic resonance and superconducting gap in unconventional superconductors. Nature Physics. 2009; 5: 873.
- Ghigo G, Ummarino GA, Gozzelino L, Gerbaldo R, Laviano F, Torsello D, Tamegai T. Effects of disorder induced by heavy-ion irradiation on (Ba1−x Kx )Fe2As2 single crystals, within the three-band Eliashberg s± wave model. Sci Rep 2017; 7: 13029.
- Ummarino GA, Gonnelli RS. Breakdown of Migdal’s theorem and intensity of electron-phonon coupling in high-Tc superconductors. Phys Rev B. 1997; 56: 14279.
- Ummarino GA, Gonnelli RS. Real-axis direct solution of the d-wave Eliashberg equations and the tunneling density of states in optimally doped Bi2Sr2CaCu2O8+x. Physica C Superconductivity. 1999; 328: 189.
- Ummarino GA, Gonnelli RS. Two-band Eliashberg equations and the experimental Tc of the diboride Mg1−xAlxB2. Physica C Superconductivity. 2000; 295: 341-348.
- Ummarino GA, Gonnelli RS, Daghero D. Tunneling conductance of SIN junctions with different gap symmetries and non-magnetic impurities by direct solution of real-axis Eliashberg equations. Physica C Superconductivity. 2002; 377: 292.
- Cappelluti E, Ummarino GA. Strong-coupling properties of unbalanced Eliashberg superconductors. Phys Rev B. 2007; 76: 104522.
- Jutier F, Ummarino GA, Griveau JC, Wastin F, Colineau E, Rebizant J, Magnani N, Caciuffo R. Possible mechanism of superconductivity in PuCoGa5 probed by self-irradiation damage. Phys Rev B. 2008; 77: 024521.
- Ummarino GA, Caciuffo R, Chudo H, Kambe S. Energy scale of the electron-boson spectral function and superconductivity in NpPd5Al2. Phys Rev B. 2010; 82: 104510.
- Varelogiannis G. Solid State Communications. 1998; 107: 427.
- Musaelian KA, Betouras J, Chubukov AV, Joynt R. Mixed-symmetry superconductivity in two-dimensional Fermi liquids. Phys Rev B. 1996; 53: 3598.
- Bok JM, Bae JJ, Choi HY, Varma CM, Zhang W, He J, Zhang Y, Yu L, Zhou XJ. Quantitative determination of pairing interactions for high-temperature superconductivity in cuprates. Sci Adv. 2016; 2: 1501329.
- Ummarino GA. Multiband s± Eliashberg theory and temperature-dependent spin-resonance energy in iron pnictide superconductors. Phys Rev B. 2011; 83: 092508.
- Vidberg H, Serene J. Solving the Eliashberg equations by means ofN-point Padé approximants. J Low Temp Phys. 1977; 29: 179.
- McMillan WL. Transition Temperature of Strong-Coupled Superconductors. Phys Rev. 1968; 167: 331.
- Hwang J, Schachinger E, Carbotte JP, Gao F, Tanner DB, Timusk T. Bosonic Spectral Density of Epitaxial Thin-Film La1.83Sr0.17CuO4 Superconductors from Infrared Conductivity Measurements. Phys Rev Lett. 2008; 100:137005.
- Sato NK, Aso N, Miyake K, Shiina R, Thalmeier P, Varelogiannis G, Geibel C, Steglich F, Fulde P, Komatsubara T. Strong coupling between local moments and superconducting ‘heavy’ electrons in UPd2Al3. Nature. 2001; 410: 340.
- Szewczyk KA, Szczesniak R, Szczesniak D. Annalen der Physik. 2018; 530: 1800139.
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?

PTZ: We're glad you're here. Please click "create a new query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."


 Save to Mendeley
Save to Mendeley