Surface energy for nanowire

The theory of surface phenomena in the production of micro-and nanocylinder for important cases is considered. Analytical solution to Gibbs–Tolman–Koenig–Buff equation for nanowire surface is given. Analytical solutions to equations for case the cylindrical surface for the linear and nonlinear Van der Waals theory are analyzed. But for a nonlinear theory, this correspondence is absent.

Introduction

In this article, the surface tension in nanowires production by the Taylor–Ulitovsky method is studied. Surface tension is a fundamental thermodynamic parameter that significantly influences the creation of nanowires.

The chemical and physical properties of interphase boundaries in nanowires, as well as for nanoparticles, have been studied in a huge number of publications (see [1], fundamental monographs [2-5], and literature [6-21], and also my researches [22-28]. We can single out the following theoretical approaches: Gibbs–Tolman–Koenig–Buff equation method ends the linear and nonlinear Van der Waals theory.

The study aims at derivation and detailed analysis of expressions for the surface tension for the microwire in thermodynamic equilibrium on the Gibbs–Tolman–Koenig–Buff equation method and on the Van der Waals theory.

The given theory can find application in microwire production technology Figures 1,2.

Figure 1: Process of casting glass-coated amorphous magnetic micro- and nanowires.
1. Cylindrical zone. 2. Cone zone.

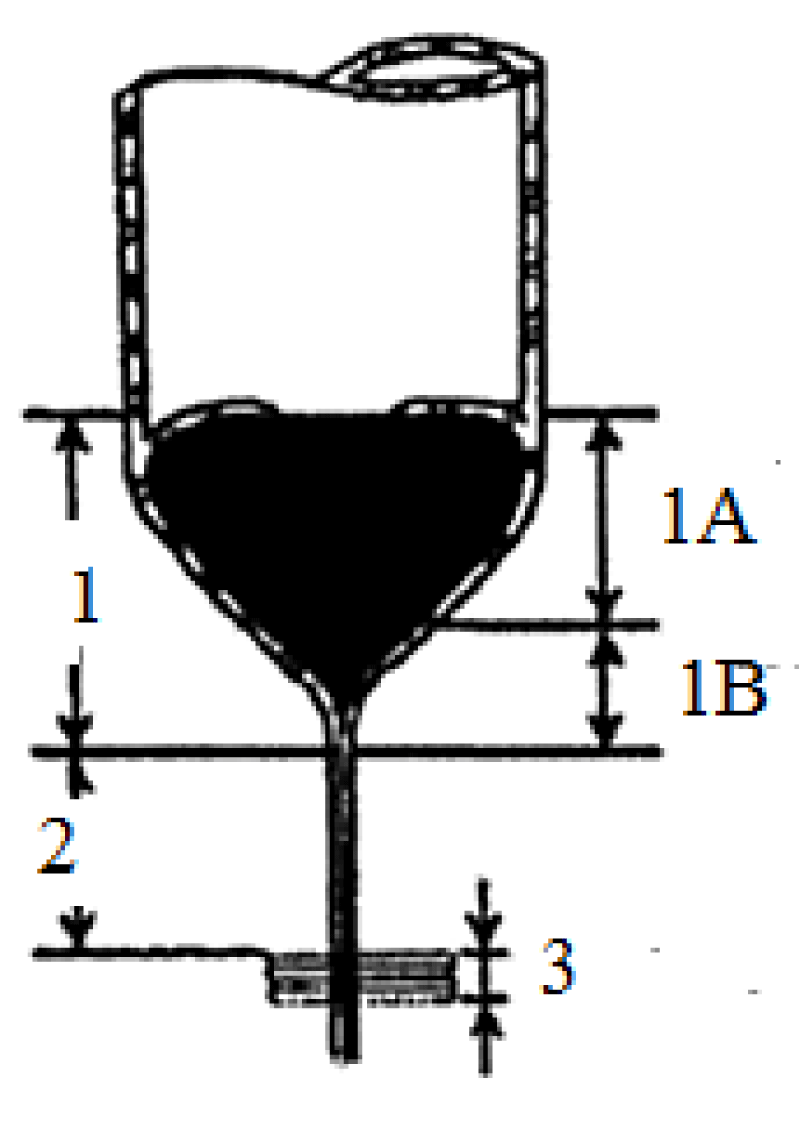
Figure 2: Drawing of micro- and nanowire fabrication process by the Taylor–Ulitovsky method.
1. Microbath: 1A). Primary cone of microbath. 1B). Secondary cone of microbath. 2. Extension zone. 3. Crystallizer.

As you can see from the figures, we must study cylindrical and conical surfaces.

Modeling of surface energy for microwires in Gibbs–Tolman– Konig–Buff`s theory

We will use the Gibbs – Tolman – Koenig – Buff differential equation [2-6] (for a cylinder) to describe the surface tensions, σ_i, of nanowires [1]:

$\frac{d\ln {\sigma }_i}{d\ln R_i}=\frac{\frac{2{\delta }_i}{R_i}+{\left(\frac{{\delta }_i}{R_i}\right)}^2}{2+\frac{2{\delta }_i}{R_i}+{\left(\frac{{\delta }_i}{R_i}\right)}^2}\text{ (1)}$

Where R_i is the radii of micro-and nanowires (the radius of its metallic kernel, R_m, or the total radius of glass, R_g).

Non-negative parameters (Tolman length), δ_i, characterize the thickness of the interfacial layer (for example, between glass and glass-metal).

In surface thermodynamics, the Tolman length is used as a parameter that is equal to the distance between the surface of tension and the equimolar surface. The numerical values of parameter the analog

"Tolman length" for micro and nanowire is in the range from 0.1 to 1 µm.

The integral in (1) (if δ_i =const.) can be exactly taken. The final result has the form [7,10]:

$\sigma /{\sigma }^{(\infty )}=\frac{R}{\delta }\sqrt{\frac{2}{2{(R/\delta )}^2+2R/\delta +1}}\exp \left(-\text{arctg}\left(\frac{1}{1+2R/\delta }\right)\right)\text{ (2)}$

The well-known Tolman formula (for cylinder) is a special case $R>>\delta$ for this formula (2)

$\sigma /{\sigma }^{(\infty )}~\frac{1}{1+\frac{\delta }{R}}\text{ (3a)}$

In case $R<<\delta$ :

$\sigma /{\sigma }^{(\infty )}~0.645(R/\delta )\text{ (3b)}$

We represent the Rusanov linear formula [5,11] for the cylindrical surface Figure 3.

Figure 3: Functions graphs of solutions (3) (dashed line), and of solutions (10 -14) (bold line) are presented. Experimental data for the surface tension of metal-glass are presented depending on the radius of the metallic kernel, Rm.

Modeling of surface energy for Micro- and Nanowires in linear Van der Waals theory

The basic equation of the linear Van der Waals theory of an inhomogeneous medium (see [1-3] for details) can be written in the form:

$n^{″}+\frac{n^{\prime }}{r}-\frac{1}{{\delta }^2}(n-n_{1,2})=0\text{ (4)}$

Where n (x) is the function when proportional to the volume density N(x) (x = r/δ, n_o=const.), $\delta$ is the radial variable measured from the center of a nanoparticle, is the Tolman length [1-3].

The general solution to Eq. (4) has the form

$n(r)=n_{1,2}+A{I}_0(r/\delta )+B{K}_0(r/\delta )\text{ (5)}$

Where $I_0(r/\delta ),K_0(r/\delta )$ is a modification to Bessel and Hankel functions?

$n(0)=n(R)=n_1,n(+\infty )=n_2\text{ (6)}$

We will accept the volume density function, N(r/δ). We get:

$N(r/\delta )\to n(0)\equiv n(R)=1,N\left(+\infty \right)\to n(+\infty )=0\text{ (7)}$

Substituting solution (5) into expression (7) and integrating, we obtain:

$N(r/\delta )=\{\begin{array}{l}1,r\le R,\\ \frac{K_0(r/\delta )}{K_0(R/\delta )},r>R,\end{array}\text{ (8)}$

Solution (8) can be used for calculating adsorption, which is defined as the excess number of atoms or molecules in the surface layer of the nanoparticle per unit area:

$\Gamma \to \delta \text{}\frac{K_1(x)}{K_0(x_0)}\text{ (9)}$

(x = r/δ, x0 = R/δ).

Taking into account adsorption (9), we obtain the differential equation

$\frac{d\ln \sigma }{d\ln x}=\frac{1}{x\{K_0(x)/K_1(x_0)\}+1}\text{ (10)}$

if х >> 1

$\frac{K_0\left(x\right)}{K_1\left(x_0^{}\right)}\to 1\text{ (11)}$

We obtain

$\frac{d\ln \sigma }{d\ln x}=\frac{1}{x+1}\text{ (12)}$

(see formula (2) and (3a));

and if x << 1

$\frac{K_0\left(x\right)}{K_1\left(x\right)}\approx x\ln \frac{2}{\gamma x}\text{ (13)}$

Where γ = 1,781 is Euler constant, we obtain

$\frac{d\ln \sigma }{d\ln x}=\frac{1}{x\ln \frac{2}{\gamma x}+1}\text{ (14)}$

This equation is integrated numerically.

Modeling of surface energy for Micro-and Nanowires in nonlinear theory

The nonlinear equation can be written in the form

${\text{n}}_1{}^{″}+\frac{1}{r}{\text{n}}_1{}^{\prime }+\frac{1}{{\delta }_1{}^2}\exp \{-{\text{n}}_1\}=0\text{ (15)}$

The simple volume density function, N, may be determined:

$N_1=1+2\ln [1-X_1{}^2]\text{ (16)}$

$X_1=\text{r}/\text{(2}\sqrt{2}{\delta }_1)\text{ (17)}$

The results obtained have a physical meaning only as long as the function N1 is positive.

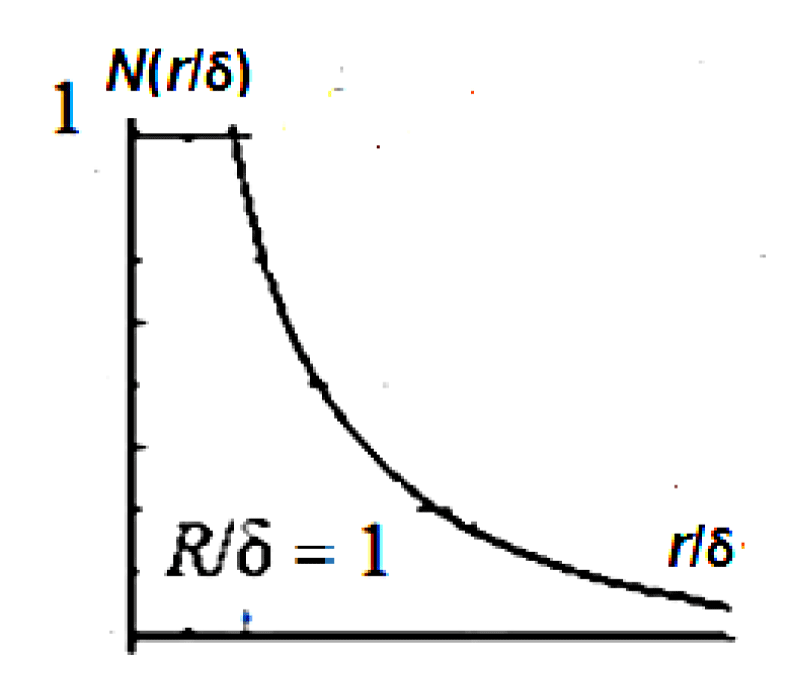
The resulting density profile (see Figure 4 and (16), (17)) is very different from the results of the linear theory (see Figure 5 and (8)), and therefore the GTKB theory (see (2), (3a), (3b)).

Figure 4: Function graph of solution (16) is presented.

Figure 5: Function graph of volume density function, N(r/δ) is presented.

Micro and nanowire will only be produced for a limited metallic kernel, R_m.

The density profiles in [13] (see Figure 6) are very different too from the results in Figure 4.

Figure 6: Qualitative density profiles of volume density function, N(r/δ) presented in [13].

Modeling of surface energy for Micro-and Nanowires in the pure case theory

The equation can be written (in the pure case theory) in the form:

${\text{n}}_2{}^{″}+\frac{1}{r}{\text{n}}_2{}^{\prime }=0\text{ (18)}$

A particular solution for equation (18) can have the form:

$n_2=c\ln (\text{R}/\delta )\text{ (19)}$

We will accept the initial values

${\text{N}}_{2,}{}_0=1\text{ (20)}$

and get

$N_2=1+\ln (\text{R}/\delta )\text{ (20a)}$

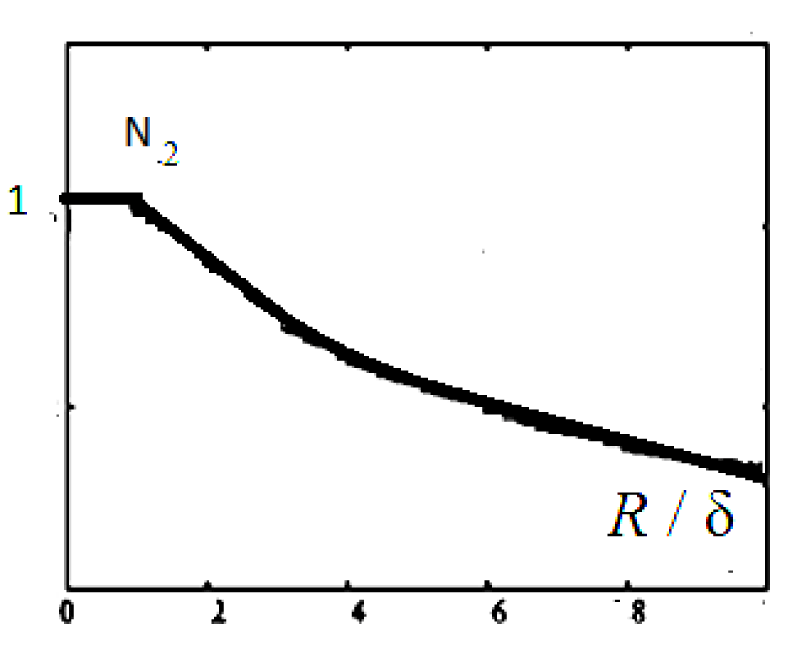
Function graph N₂ is shown in Figure 7.

Figure 7: Function graph of solution (20-20a) is presented.

Conclusion

A feature of micro-and nanowires is that these objects consist of an amorphous alloy core (metal conductor) with a diameter of (0.1...50) µm, covered with a Pyrex-like coating with a thickness of (0.5...20) µm. Therefore, the main technological parameter for the production of glass micro-and nanowires is the surface tension of the surfaces of micro-and nanowires.

According to the previous analysis [1], the most significant effect on the geometry of such microwires comes from the glass properties. The microwire radius R_g (the outer radius of the glass shell) is estimated as follows [1]:

$R_g~\frac{{\text{η}}^{2-k}}{V_d^k{\text{σ}}_s^{1-k}}\text{ (21)}$

Where k is the parameter, which is dependent on a casting rate (0 < k < 1); V_d is the casting rate; σ_s is the surface tension.

The metallic radius, Rm, is possible to estimate approximately:

$R_m~\frac{{\sigma }_{sm}^{}}{V_d^{2-k_m}}\text{ (22)}$

σ_sm is the surface tension of metal – glass (0 < k_m< 1).

We thus confirm that surface tension, defined as excess free energy per unit surface area, determines the radius of micro-and nanowires.

1. Baranov SA, Larin VS, Torcunov AV. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals. 7: 136.
2. Ono S, Kondo S. Molecular Theory of Surface Tension in Liquids, in Structure of Liquids, series Encyclopedia of Physics, Springer, Berlin, Heidelberg. 1960; 3/10: 134–280.
3. Rowlinson JS, Widom B. Molecular Theory of Capillarity, Oxford University Press, Oxford, 1989.
4. Jaycock MJ, Parfitt GD. Chemistry of Interfaces, Halstead Press, John Wiley & Sons, New York, 1981.
5. Rusanov AI, Prokhorov VA. Interfacial Tensiometry, Elsevier. Amsterdam. 1996.
6. Tolman RCJ. The Effect of Droplet Size on Surface Tension. Chem Phys. 1949; 17 (3): 333.
7. Rekhviashvili SSh, Kishtikova EV. Tech Phys. 2011; 56(1): 143.
8. Rekhviashvili SSh. Colloid J. (2020); 82(3): 342.
9. Sokurov AA, Vestnik Kraunc, Ser. Fiz.-Mat. Nauk. 2018; 23(3): 140.
10. Rekhviashvili SSh, Sokurov AA. Turk J Phys. 2018; 42: 699.
11. Rekhviashvili SSh. Razmernye iavlenia v fizike kondensirovannogo  sostoianiia I nanotehnologiah. Nalchik 2014; 250.
12. Bykov TV, Zeng XC. J Chem Phys. 2001; 105 (47): 11586.
13. Bykov TV, Shchekin AK. Inorg Mater. (Transl of Neorg Mater). 1999; 35: 641.
14. Hadjiagapiou IA. J Phys: Condens Matter. 1995; 7: 547.
15. Kalikmanov VI. J Chem Phys. 2004; 121: 8916.
16. Schmelzer JWP, Ropke G, Priezzhev VB. Nucleation Theory and Applications, JINR Publishing House, Dubna. 1999.
17. Schmelzer JWP, Baidakov VG, Boltachev GSh. J Chem Phys. 2003;119: 6166.
18. Baidakov VG, Boltachev GSh. Phys Rev 1997; E 59(1): 5648.
19. Baidakov VG, Boltachev GSh. Phys Rev E.  1999; 59: 469.
20. Baidakov VG, Protsenko SP, Chernykh GG, Boltachev GSh. Phys Rev E.  2002; 65: 047601.
21. Vov PEL, Svetukhin VV. Phys Stat Sol. 2015; 57: 1213.
22. Baranov SA. In Handbook of Nanoelectrochemistry: Electrochemical Synthesis Methods, Properties and Characterization Techniques, Springer, International Publishing, Switzerland. 2015; 1057–1069.
23. Baranov SA, Rekhviashvili SSh, Sokurov AA. Surf Eng Appl Electrochem.  2019; 55(3): 286.
24. Baranov SA. Surf Eng Appl Electrochem. 53(2): 124.
25. Baranov SA.  Mold J Phys Sci. 2020; 19(1–2): 182.
26. Baranov SA. Mold J Phys Sci. 2021; 20(1–2):44.
27. Baranov SA. J Anal Tech Res. 2021; 3(2): 28.
28. Baranov SA.  J Anal Tech Res. 2021; 3(2): 39.