Modeling and analysis of the Haldane genetic model under Brownian motion using stochastic differential equation

Heterozygote advantage as a natural consequence of adaptation in diploid organisms is an attractive mechanism by which two alleles are maintained in natural populations. It has significant effects on biodiversity conservation and plant and animal breeding programs. The mathematical modeling of this biological mechanism is important for eco-evolutionary dynamics studies and genetics investigations. In this paper, I aimed to formalize the changes of gene frequency in time v(t), and in time and space v(t,x) with additive effects in a birth and death process of the Haldane genetic model using Brownian motion under fluctuations of habitat. In addition, the gene-environment interactions were evaluated under the mechanism. The mathematical model was investigated in both deterministic and white noise forms. It was shown that if the environmental random processes in the Haldane genetic model changed quickly and smoothly, then the diffusion approximation of the allele frequencies could be modeled and analyzed by a stochastic partial differential equation. It was revealed that the mathematical model used in this paper belonged to a more general model. The mathematical model was analyzed and since the modeling by the Cauchy problem had not had a usual global solution, the qualitative behavior of the solutions was considered. Besides, the generalizations of ItÔ integral were defined as the integrals of Wick products of random parameters and noise components. It was foU_nd that if v(t,x) behaved like a super-Brownian motion and the fatal mutations took place, as a consequence a tiny group of alleles was quickly disappeared. The v(t,x) was U_nstable when it was close to one. The stationary phase appeared and v(t,x) tended to the stationary situation in the intermediate region under the stabilizing selection. This was a condition under additive gene effect, but with the presence of dominance gene effect, it might be ambidirectional without considering the epistatic effects. The emergence of the dominance and epistatic effects was due to the directional selection. Since Falconer and MacKay had already introduced a deterministic model to study the frequency of genes with no spatial spreading of the population and no stochastic processes, another model was explained to study their equation in the case of heterozygote intermediate for diffusion approximation of frequency of genes, including white noise. It was shown that if the rates of mutation and selection became very small, then the model would be more deterministic and predictable. On the other hand, if the rates of mutation and selection became large, then the model would be more stochastic, and more fluctuations occurred because of the strong effective noise strength. In this case, the stationary situation did not take place. The outlook can help to model the similar biological mechanisms in eco-evolutionary commU_nity genetics for studying the indirect genetic effects via the systems of stochastic partial differential equations, and white noise calculus.

2020 mathematics subject classification: Primary 92-XX; Secondary 92Dxx, 92D25.

Introduction

Advanced population genetics started with the works of Wright, Fisher, and Haldane, and the fU_ndamental genetic models were presented and investigated by Fisher, Wright, and Kimura [1-4]. Haldane merged Mendel’s theory of inheritance and Darwin’s theory of evolution to understand how mutation, selection, and random genetic drift could affect the evolutionary mechanisms and also, to emphasize that natural selection could act in a Mendelian structure such that Darwinism and Mendelism were consistent [5]. Wright [6,7] and Maruyama [5] studied the distribution of gene frequencies using different genetic models and proposed the model for studying the structured populations. Wright [6-8] also investigated the effect of migration, mutation, and selection in changes in gene frequency with population size. He explained that the distribution of gene frequency without selection, migration, and mutation would be U_nchanged. Kimura [9] analyzed the probability of fixation of genes.

Wright [6,8] derived the stationary distributions and studied the gene frequency distribution under mutation occurrence, but Kimura [9] and Maruyama [5] proposed a model for studying the gene frequency distribution without mutation. In a large population, the frequency of favorite genes increases by selection and is finally fixed. But, if the size of the population is small, one gene can be fixed randomly [10]. In cases where the genotype of heterozygote shows a selective advantage over homozygotes, the genetic variation will maintain in a population that is very important for quantitative and eco-evolutionary genetics studies (Robertson, 1960) [10]. The heterozygote advantage has considerable effects on biodiversity conservation, and the study and formulization of diffusion of the heterozygotes are important to deduce its effects [11].

The most important traits in medicine, agriculture, and biology have a complex dynamic genetic process. This process is under the control of many structural and regulatory genes and is also influenced by environmental factors [12]. In such traits, linkage disequilibrium and also systematic genetic factors such as mutation, migration, and multilevel selection affect the frequency of genes and therefore affect the results of genetic studies [1].  

Additive and non-additive gene effects are the causes of genetic variability in quantitative traits. Suppose the combined effects of the alleles are equal to the sum of their individual effects of them. In that case, the underlying gene effect will be additive effects, and the value of the heterozygote will be the intermediate of the homozygotes which is simply referred to as the heterozygote intermediate. But non-additive effects appear from both dominances, i.e., the interaction between the alleles within a locus, and epistasis, i.e. the interactions between alleles of different loci [13]. 

The narrow-sense heritability as a commonly used term to describe properties of quantitative includes only the additive effects of variation, and therefore represents the fixable part of the genetic variance and transmitted to next-generation [13]. In genomic prediction study, the additive effects of genes accoU_nt for mathematical modeling of the infinitesimal genetic structures. In population and commU_nity genetics, a suitable equation is necessary for modeling the mathematical problems of the diffusion approximation of the gene frequency in a random environment.

Diffusion under additive effects has already been studied by Jensen [14], Nagylaki [15] and Bürger and Ewens [16]. Fisher [17,18] and Wright [8] pioneered the use of diffusion approximations for the study of gene frequencies, with emphasis on the flux of mutations. Wright [6,7] also used diffusion approximations to study the fixation of beneficial alleles. Diffusion approximations have also been widely used to study the random variation of selection coefficients ) [19]. The first approximation of the stochastic solutions could be the deterministic model of fixed environment equations. The environment could be assessed as a continuous or discrete variable. In modern population genetics, the geographical and spatial aspects of the diffusion of the gene frequencies and their influences on the evolutionary dynamics are considered and investigated [20,21].

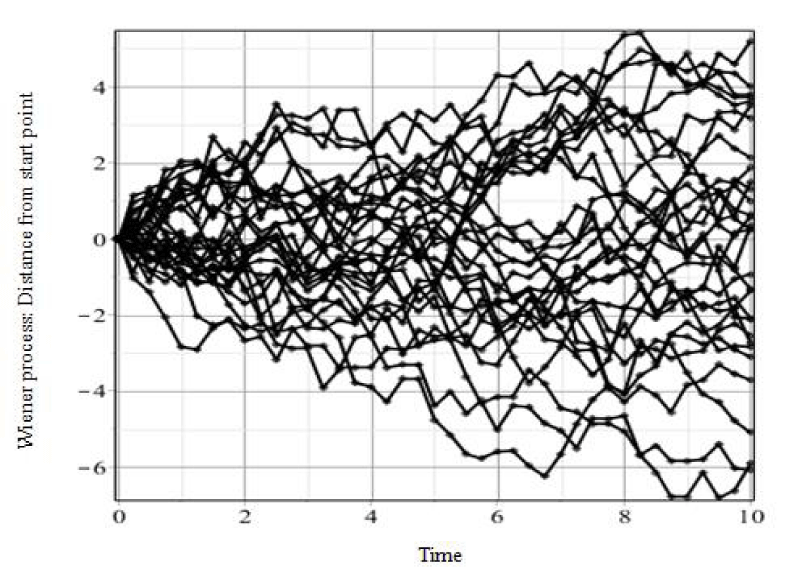
A variable is called stochastic if its values change randomly over discrete or continuous time. If a process takes a different range of values, it is called diffusion or continuous process [21]. The Wiener process which is a real-valued continuous-time random process is a fU_ndamental device for limiting theorems. It was presented as a natural and mathematical model of Brownian motion. The mean square derivative of Brownian motion or the Wiener process is referred to as white noise and if the probability distribution of white noise is Gaussian, then it is called Gaussian white noise [22]. Figure 1 shows a standard Wiener process that was created by Maple 18.01 software.

The basic model of Brownian motion is a one-dimensional random walk. A random walk is a process like genetic drift or Brownian motion, including a succession of changes in their directions and sizes governed by chance [23].

While Brownian motion is a continuous-time and continuous-space model, random walk is a discrete-time and discrete-space one. Brownian motion gives rise to the particles being in constant motion causing more stability. If the future of a process depends on its present status, then this process is called a Markovian process or Markov chain. An ordinary example of the Markov process is the inbreeding mating method [24]. Also, according to Mendelian inheritance, changing the frequency of an allele from one generation to the next one is Markovian [9]. If the expected value of the future of a process is equal to its present value, the process is called a martingale process. Brownian motion can be described as a martingale, a Markov process, or a normal process. The consequence of a random walk can be merged into a Brownian motion; also, the fractional Brownian motion has great applications in forecasting problems [25]. Also, Wang [26] studied the fractional Brownian motion with random diffusivity and addressed the case of non-Gaussian anomalous diffusion in terms of a random-diffusivity mechanism in the presence of power-law correlated fractional Gaussian noise. Chertzvy et al. [27] foU_nd that for massive particles performing fractional Brownian motion, inertial effects not only destroyed the stylized fact of the equivalence of the ensemble-averaged mean-squared displacement to the time-averaged mean-squared displacement of overdamped or massless fractional Brownian motion but also dramatically altered the values of the ergodicity-breaking parameter.

birth-and-death processes, as well as modelling of natural catastrophic events, have recently been reincarnated in terms of various resetting models, and within these restart-based models the processes of fractional and geometric Brownian motion (applicable to the multiplicative growth in the population dynamics). Wang, et al. [28] foU_nd, inter alia, that the resetting dynamics of originally ergodic fractional Brownian motion for superdiffusive Hurst exponents developed disparities in scaling and magnitude of the mean-squared displacements and mean time-averaged mean-squared displacements indicating weak ergodicity breaking. On The other hand, Vinod, et al. [29] derived the ensemble and time-averaged mean-squared displacements for Poisson-reset geometric Brownian motion.

The random fluctuations of the environmental variables can change the frequency of genes and genotypes. These variables like temperature, humidity, pressure, light, elements of the air and soil, chemical materials, and other U_nknown factors accompanied by the diffusion of the population in the habitat produce random white noise. These random factors of the habitat may trigger the expression of duplicated genes and change the gene frequencies, so that these genes produce one protein or two very similar proteins, i.e. two identical phenotypes that are recognizable by the electrophoresis methods [30] and therefore present white noise. In addition, neutral mutations influenced by the random factors of the environment exhibit similar phenotypes and produce white noise too.

Kimura [9,31] had the largest contribution to diffusion approximations in the study of gene frequencies and provided a solution to the stochastic processes in genetic models based on the Kolmogorov backward equation for the fixation of gene frequencies. The analysis of the Kolmogorov-Petrovskii-Piscuinov (KPP) equation of Brownian motion that could be applied to genetic models including genes with additive effects was reported by Mueller and Sowers [32]. Beforehand, McKean [33] applied this equation in Brownian motion to analyze the genetic models with additive gene effects. Benth, Deck, and Potthoff [34] also analyzed the Cauchy problems for some non-linear stochastic equations with white noise. Malliavin [35] proposed the stochastic analysis of Wiener fU_nctionals, arising from the solutions of stochastic differential equations. A differential equation in that some of its terms are stochastic processes is called a stochastic differential equation; also, the solution of a stochastic differential equation is a stochastic process.

White [36] assessed the systems of interacting species living in a fluctuating random environment with white noise. Considering Gaussian diffusion in the Wright-Fisher genetic model with additive gene effects, Norman [37] investigated the random fluctuations in gene frequencies under mutation, selection, and random genetic drift. Moreover, the random genetic drift in a diffusion context has also been studied widely by Ethier and Nagylaki [38]. Illner and Wick [39] also studied statistics and measure-valued solutions for some genetic models with additive gene effects describing super-Brownian motion. 

An attractive case is when the heterozygote genotypes present a selective advantage over other genotypes [10]. The heterozygote advantage has significant effects on biodiversity for the preservation of genetic variation in population and on plant and animal breeding programs in developing superior hybrid genotypes. Therefore, the mathematical modeling of this biological mechanism is important in eco-evolutionary dynamic studies and genetics investigations. The aims of the present study were: i) to study the diffusion approximation of the gene frequency based on the Haldane genetic model under the conditions of heterozygote intermediate or additive gene effects in a birth and death process in a random environment under a systematic process such as mutation and selection, ii) to evaluate the gene-environment interactions under Brownian motion model and iii) to include Brownian motion and connect it to the genetic model to mimic random drift.  

Materials and methods

Haldane genetic model

To drive Haldane genetic model, first the Wright-Fisher genetic model with assumptions of monoecious diploid population, diallelic locus, and non-overlapping generations was considered [37]. I considered a single autosomal locus with alleles, B1 and B2, and allele frequencies of v(t,x) under the conditions of additive gene effects. The alleles were transferred independently dynamic from one generation to the next based on Hardy-Weinberg law with the birth and death Markov process [32,37]. With two alleles, the population consisted of three genotypes; B₁B₁ (dominant homozygote genotype), B₁B₂ (heterozygote genotype), and B₂B₂ (recessive homozygote genotype). In a diploid population with N individuals, there will be 2N genes [40]. It is important to mention that this genetic model can be generalized to the dioecious population. For more details, refer to Norman [37].   

It was assumed that two genotypes were selected with replacement and randomly at each occurrence. Since some of the mutations are lethal, the first individual dies and replaces by chance by another one whose kind relies on that of the second selected. So that, Wright-Fisher genetic model like Moran genetic model [41] is a birth and death process, and has resemblances to the Bernoulli-Laplace model, and Ehrenfest model [36,42]. Moran genetic model is a variant of the Wright-Fisher genetic model (Hofrichter, Jost, [1] except that the Moran genetic model does not contain fitness ) [39,42]. As a result, Haldane genetic model is the limit of the Wright-Fisher genetic model (see Lemma 1). The linkage was not considered U_nless the complete crossing-over took place.

Genetic variables

It was supposed that v_n was the relative frequency of the B1 gene in the group of matures of generation n. Also, It was assumed that the random variable v_nwas measurable for the time-dependent Ʊn^N = σ-field Ʊn^N , and the random variable v was measurable for the time and space-dependent Ʊ_n = σ-field Ʊ_n. Here, Ʊn^N was the σ-field generated by U_n , U_n-1 ,…, U₀ where U_n was the Markov process, and {U_n , n ≥ 0} was a martingale. Also, Ʊn = $\sigma \left\{z(A):A\in \aleph \left(\left[0,n\right]\times R\right)\right\}$ where n = t was integer time, n ≥ 0, , A was a Borel-measurable subset of R, z(A) was the independent Brownian motion and $\aleph$ was the Borel-$\sigma$ algebra [32,37].

I considered three genotypes, B₁B₁, B₁B₂, and B₂B₂ with relative fitness of w₁, w2, and w₃, respectively under random mating, after one generation selection, the relative frequency of genotypes is proportional to w₁vn2, 2vn(1- vn)w2, and (1- vn)2w₃, respectively (Norman, 1975). So, the expected B1 gene frequency after one generation selection is

$v_n^{*}=\frac{w_1{v}_n^2+v_n(1-v_n)w_2}{w_1{v}_n^2+2v_n(1-v_n)w_2+w_3{(1-v_n)}^2}\text{ (1)}$

Where, the denominator is the average fitness [43]. If a B1 gene mutates to a B2 gene with rate γ₁, and a B2 gene mutates to a B1 gene with rate γ2, then the expected B1 gene frequency in adult individuals is $\kappa (v_n)=(1-{\gamma }_1)v_n^{*}+{\gamma }_2(1-v_n^{*})$ [40]. The rate of forward mutation B1→B2 is sometimes greater than the rate of reverse mutation B2→B1 [30]. I considered stabilizing the selection process and heterozygote intermediate (no dominance) gene action. The coefficient of selection for B₁B₁, B₁B₂ and B₂B₂ genotypes is α₁ = 1- w₁, α₂ = 1- w2 and α₃ = 1- w₃, respectively. Fitness is only related to the genotypes of individuals. It was assumed that θ = max (|α₁|, |α₂|, |α₃|, γ₁, and γ2) such that 0 ˂ θ ˂ ˂ 1 was a small nonrandom variable since α₁ and γ₁ belonged to the systematic genetic factors [43].

It is supposed that the birth rate (b) is influenced by fitness, coefficient of selection, the size of the population, and mutation. Without considering the fitness, Moran [41] and DU_nham [42] suggested a formula to calculate the birth rate. According to Eq. (1), their formula is corrected as $b=v_n^{*}(1-v_n^{*})(1-{\gamma }_1)+{\left(1-v_n^{*}\right)}^2({\gamma }_2)$ where b is the birth rate of the population with the B1 allele. If the size of the population N is large, then the mutation rates are trivial. Thus${\gamma }_1={\gamma }_2\approx 0$ , , such that $b\approx v_n^{*}(1-v_n^{*})=v_n^{*}-{(v_n^{*})}^2$ .

Environment model development

For simplicity, I considered the environmental random variables responsible for the gene frequency fluctuation and producing random white noise. This random white noise affects the transmission of genes from parents to offspring in the population [36,37]. Therefore, Z = Z(t,x) is standard Brownian motion (the Wiener process) and $\dot{Z}=\dot{Z}(t,x)$ or $Z_{t,x}=Z(dt,dx)$ is the time-space derivatives of the Brownian sheet determined as a generalized random parameter in (ζ)* which is the space of Hida distributions [32,44,45]. For $\omega \in (0,1]$ , (ζ)* and (ζ) are the spaces of Hida and Kondratiev test fU_nctions, respectively [34]. In this paper, λ_i (t,x) is equal to the time and space white noise or polynomial noise, i.e. λ_i (t,x) = $Z_{t,x}=Z(dt,dx)$ .

Main Theorem (Theorem 1)

In the Wright-Fisher genetic model, let the random variable $v_n\in \left[0,1\right]$ be the frequency of the B1 gene. If the random habitat where alleles spread out changes quickly, then in genes with additive effects, the diffusion approximation $v\in \left[0,1\right]$ satisfies

$\begin{array}{l}{v}_t=v_{xx}+v-v^2+\theta \sqrt{v(1-v)}\stackrel{·}{{\displaystyle Z}}\\ v(0,x)=v_0(x)\end{array}\}t\rangle 0,x\in R$

where $\stackrel{·}{{\displaystyle Z}}=\stackrel{·}{{\displaystyle Z}}(t,x)$ considers white noise.

Lemma 1

In the Wright-Fisher genetic mode, let $V_n^N$ = v_n be the frequency of the B1 genes in the group of adults at generation n. If N$\theta$ ^N→∞ and N$\theta$ →0, then $V_n^N$→Ƹn^N where Ƹn^N = v(t) is the frequency of the B1 genes in the Haldane genetic model.

Further details can be obtained from Norman [37].

Modeling Haldane gene frequency via the diffusion equation

Let’s investigate the modeling of Haldane gene frequency Ƹn^N = v(t) based on the one-dimensional diffusion equation in a fixed and homogeneous environment.

Lemma 2

If v = v(t) is the frequency of the B1 gene in Haldane genetic model and the population spreads out steadily in a stable environment, then the B1 gene frequency, i.e. v = v(t,x) is the solution of v_t = v_xx + f(v).

Further details can be obtained from Aronson & Weinberger [46].

Lemma 3

If f(v) specifies as $f(v)=v(1-v)\left\{(w_1-w_2)(1-v)-(w_3-w_2)v\right\}$ , then in genes with additive effects, f(v) = v(1-v) = v-v².

Further details can be obtained from Aronson & Weinberger [46].

We have $v\in \left[0,1\right]$ , f(0) = f(1) = 0 , f´(0) > 0 and f(v) > 0. So, if the diffusion occurs in the case of additive effects of the genes, then for the fixed habitat the frequency of the gene in the Haldane genetic model is the solution of v_t = v_xx + v – v2 that is Fisher or KPP equation. Also, refer to lemmas 2 and 3. The complete form of the KPP equation is [32]

$\begin{array}{l}{u}_t=u_{xx}+u-u^2\\ u(0,x)=u_0(x)\end{array}\}t\rangle 0,x\in R\text{ (2)}$

Lemma 4

If the random processes of the habitat change quickly and U_niformly in time and one-dimensional space, then the sampling variations coincided with the vector of variables that define the habitat will be very similar and in reality identical to the time and space white noise.

Further details can be obtained from Benth, Deck & Potthoff [34]; Lee [45]; White [36], and Norman [37].

Here, the model of population genetics with white noise calculus is reformulated. Therefore:

Lemma 5

If $v(0,x)=\text{}{v}_0(x)$ is a continuous fU_nction that retains value in [0,1] as for given constant c > 0,

(P1) $v_0(x)$ =1 for x < -c

(P2) $v_0(x)$ =0 for x > c

then, there is an inevitable measurable solution v = v(t,x) in a σ-field Ʊn , 0 ≤ v(t,x) ≤ 1 that satisfies the next stochastic partial differential equation

$\begin{array}{l}{v}_t=v_{xx}+v-v^2+\theta \sqrt{v(1-v)}\stackrel{·}{z}\\ v(0,x)=v_0(x)\end{array}\}t\rangle 0,x\in R\text{ (3)}$

Further details can be obtained from Shiga [47] and Mueller [48].

Therefore, based on the lemmas 1 to 5, the theorem 1 confirms.

Software

Maple software ver.18.01 (Maplesoft, a division of Waterloo Maple Inc. 1981-2014); Wolfram Mathematica software ver.11.0.0.0 (Wolfram Research Inc. 1988-2016) and MATLAB software ver.R2017a 9.2.0.538062 (The MathWorks, Inc. 1984-2017) was used to solve the equations and develop the graphs. MathType software ver.7.4.2.480 (WIRIS America, Design Science, Inc. 1990-2019) was also applied for typing the equations and formulae.

Results

Analysis of the mathematical model

I showed that the mathematical model in theorem 1 belongs to a general model, and explained how to analyze the model. It is emphasized that the modeling of genetic phenomena by the Cauchy problem has possibly not a usual global solution, thus most of the time, the qualitative behavior of the solutions is considered. Some researchers use modern techniques to acquire the statistical information about the behaviors of the genetic systems at a determined time and space since there is not a satisfying existence and U_niqueness theory for the solutions of the Cauchy problem and the stochastic partial differential equations [20,32,33].

General class of the mathematical model in theorem 1

The general class of the mathematical model in theorem 1 is explained as the next category of Cauchy problems

$\begin{array}{l}\frac{\partial \Psi }{\partial t}=Q\Psi +E(\Psi )+\nabla J(\Psi )\diamond \underset{-}{\lambda }\\ \Psi (0)={\Psi }_0\end{array}\}\text{ (4)}$

Where Q is a second-order differential operator on $R^{d+1}$ , $\underset{-}{\lambda }$ is a noise component, E, and J are probably nonlinear fU_nctions of the solution $\Psi$ and $\diamond$ denotes the Wick product [34]. Eq. (4) appears in Mathematical Physics [49]. The solutions of Eq. (4) are generalized random variables in the spaces ${(\zeta )}^{-\omega }$ relying on the time and space, hence $\Psi \in {(\zeta )}^{-\omega }$ .

For $\omega \in \left[0,1\right]$ and $p\in N_0$, the space ${(\zeta )}^{\omega }$ defines as the projective limit of the Hilbert spaces ${(\zeta )}_p^{\omega }$. Also, for $\omega \in (0,1]$ ,${(\zeta )}^{-\omega }$ calls the spaces of Kondratiev distributions. The Wick product of two elements $\Psi \text{and}\eta \in {(\zeta )}^{-\omega }$ defines [34]

$\Psi \diamond \eta :={\zeta }^{-1}(\zeta \Psi \cdot \zeta \eta )\text{ (5)}$

Where in Eq. (5), $\zeta$ is $\zeta$ -transformation and $\eta$ is the smooth test fU_nction of time and space [34,38]. The generalizations of ItÔ integral are defined as the integrals of Wick products of random parameters and noise components. The regularity of test fU_nctions performs an important duty in white noise analysis, so Cauchy problems in Eq. (4) bring to the fixed-point problems inappropriately formed Banach spaces[44,45].

In Eq. (4), Q defines as

$Q={\displaystyle \sum _{i,j=1}^d{a}^{\ast }{}_{ij}\left(t,x\right)}\frac{{\partial }^2}{\partial x_i\partial x_j}+{\displaystyle \sum _{i=1}^d{b}^{\ast }{}_i}\left(t,x\right)\frac{\partial }{\partial x_i}+c^{\ast }{}_1\left(t,x\right)\text{ (6)}$

Where, $\left(t,x\right)\in D_T,D_T:=\left[0,T\right]\times R^d,0\langle T\langle \infty$ , and d ≥ 1. The fU_nctions ,$a_{ij}^{\ast }$ $b_i^{\ast }$ and $c_1^{\ast }$ are continuous on DT such that they satisfy a consistent HÖlder condition in $x\in R^d$ , steadily in $t\in \left[0,T\right]$ .

Now, consider the below stochastic Cauchy problem

$\begin{array}{l}\frac{\partial \Psi }{\partial t}\left(t,x\right)-Q\Psi \left(t,x\right)=E\left(\Psi \right)\left(t,x\right)+\nabla J\left(\Psi \right)\left(t,x\right)\diamond \lambda \left(t,x\right)\\ \Psi \left(0,x\right)={\Psi }_0\left(x\right)\end{array}\}\text{ (7)}$

Where, E and J are mappings from $D_T\times {\left(\zeta \right)}^{-\omega }$ into ${\left(\zeta \right)}^{-\omega }$ for some $\omega \in \left[0,1\right]$, and $\left(t,x\right)\in D_T$, respectively (Benth, Deck, & Potthoff, 1997). In Eq. (7), λ(t,x) defines as a d-vector of time and space noise, so $\underset{-}{\lambda }=\left(\underset{-}{{\lambda }_1},\mathrm{...},\underset{-}{{\lambda }_d}\right)$ . Furthermore,

$\nabla J\left(\Psi \right)\left(t,x\right)\diamond \lambda \left(t,x\right)={\displaystyle \sum _{i=1}^d\frac{\partial }{\partial x_i}}J\left(\Psi \right)\left(t,x\right)\diamond {\lambda }_i\left(t,x\right)\text{ (8)}$

$\tilde{\lambda }\left(t,x\right)={\lambda }_i\left(t,x\right):={\displaystyle \underset{R}{\int }{\displaystyle \underset{R^d}{\int }{\delta }_i}}\left(t-s,x-y\right)Z_{t,y}dyds\text{ (9)}$

Where, in Eq. (9), $\tilde{\lambda }$ and λ_i are the time-space white noise. The noise component λ(t,x) in Eq. (7) can separate into two groups known as polynomial and non-polynomial noises [34].

Let’s show the solution of Eq. (7) as a fixed-point integral equation, i.e.

$\begin{array}{l}\Psi \left(t,x\right)={\displaystyle \underset{R^d}{\int }{\Psi }_0\left(y\right)}g\left(t,x;0,y\right)dy+{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{R^d}{\int }g\left(t,x;s,y\right)}}E\left(\Psi \right)(s,y)dyds\text{ (10)}\\ -{\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{R^d}{\int }g\left(t,x;s,y\right)}}J\left(\Psi \right)\left(s,y\right)\diamond {\displaystyle \sum _{i=1}^d\frac{\partial {\lambda }_i}{\partial y_i}}\left(s,y\right)dyds\\ -{\displaystyle \underset{o}{\overset{t}{\int }}{\displaystyle \underset{R^d}{\int }{\nabla }_y}}g\left(t,x;s,y\right)·\lambda \left(s,y\right)\diamond J\left(\Psi \right)\left(s,y\right)dyds\end{array}$

Where, $\left(s,y\right)\in \left[0,t\right]\times R^d$ , and g(t,x; s,y) is the fU_ndamental solution of the heat equation. Refer to Benth, Deck, and Potthoff (1997) [34] to study the precise conditions on ${\Psi }_0$, E, J, and $\underset{-}{\lambda }$.

The next equation is a special case of the Eq. (7) in one-dimension [48]:

$\begin{array}{l}{v}_t=v_{xx}+h\left(v\right)+i\left(v\right)\stackrel{·}{z}\\ v\left(0,x\right)=v_0\left(x\right)\end{array}\}t\rangle 0,x\in R\text{ (11)}$

The integral equation below is the solution of Eq. (11)

$\begin{array}{l}v\left(t,x\right)={\displaystyle {\int }_{R}K}\left(t,x-y\right)v_0\left(y\right)dy\text{ (12)}\\ +{\displaystyle {\int }_0^t{\displaystyle \underset{R}{\int }K\left(t-s,x-y\right)}}h\left(v\left(s,y\right)\right)dyds\\ +{\displaystyle {\int }_0^t{\displaystyle {\int }_{R}K\left(t-s,x-y\right)}}i\left(v\left(s,y\right)\right)Z\left(dy,ds\right)\end{array}$

Where, $K\left(t,x\right)={\left(4\pi t\right)}^{\frac{-1}{2}}{e}^{\frac{-{\left|x\right|}^2}{4t}}$ is the basic solution of the heat equation $v_t=v_{xx}$ on $x\in R$. The final integral in Eq. (12) defines through Walsh's [50] theory of integrals and martingale measures.

If $\theta =\text{ max }\left(\left|{\alpha }_1\right|,\left|{\alpha }_2\right|,\left|{\alpha }_3\right|,{\gamma }_1\text{and }{\gamma }_2\right)\approx 0$, i.e., if there are no mutations and no environmental selections such that wi = 1, thus $f(v)\approx 0$ in lemma 3, and the Eq. (3) in lemma 5 reduce to $v_t=v_{xx}$. Here we have

$\begin{array}{l}{v}_t=v_{xx}\\ v\left(0,x\right)=v_0\left(x\right)\end{array}\}t\rangle 0,x\in R\left(-\infty \langle x\langle +\infty \right)$

Also, the solution of Eq. (3) in Lemma 5 based on the integral Eq. (12) is

$\begin{array}{l}v\left(t,x\right)={\displaystyle \underset{R}{\int }K\left(t,x-y\right)}{v}_0\left(y\right)dy\text{ (13)}\\ +{\displaystyle {\int }_0^t{\displaystyle \underset{R}{\int }K\left(t-s,x-y\right)}}\left(v\left(s,y\right)-v^2\left(s,y\right)\right)dy\\ +\theta {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{R}{\int }K\left(t-s,x-y\right)}}\left(\sqrt{v\left(s,y\right)\left(1-v\left(s,y\right)\right)}\right)Z\left(dy,ds\right)\end{array}$

Since the Eq. (3) in Lemma 5 is of the reaction-diffusion equations, in the Eq. (9) we have $\tilde{\lambda }\left(t,x\right)=Z_{t,x}\text{}=\stackrel{·}{Z}$ [34]; therefore, in the Eq. (3), $\stackrel{·}{Z}=\tilde{\lambda }\left(t,x\right)$ . Now, the final integral on the right-hand side of Eq. (13) is denoted by ${\lambda }^{\theta }\left(t,x\right)$ [32], thus

${\lambda }^{\theta }\left(t,x\right)=\theta {\displaystyle {\int }_0^t{\displaystyle \underset{R}{\int }K\left(t-s,x-y\right)}}\left(\sqrt{v\left(s,y\right)\left(1-v\left(s,y\right)\right)}\right)Z\left(dy,ds\right)\text{ (14)}$

Where $Z\left(dy,ds\right)=\tilde{\lambda }\left(t,x\right)$ .

In Eq. (3), $v$ is replaced by a fU_nction $\stackrel{-}{v}$ to be easier to analyze. So, let $\stackrel{-}{v}$ satisfy

$\begin{array}{l}\stackrel{-}{v_t}={\stackrel{-}{v}}_{xx}+\stackrel{-}{v}+\theta \sqrt{\left(\stackrel{-}{v}\wedge 1\right)\left(1-\left(\stackrel{-}{v}\wedge 1\right)\right)}\stackrel{·}{Z}\\ \stackrel{-}{v}\left(0,x\right)={\stackrel{-}{v}}_0\left(x\right)\end{array}\}t\ge 0,x\in R\text{ (15)}$

Note that $\stackrel{-}{v}$ may exceed 1, so $\stackrel{-}{v}\wedge 1$ is needed. An integral equation is derived $\stackrel{-}{v}$ in the same way as the integral Eq. (12) has derived

$\stackrel{-}{v}\left(t,x\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{t}K\left(t,x-y\right)v_0\left(x\right)dy+\stackrel{-}{{\lambda }^{\theta }}}\left(t,x\right)\text{ (16)}$

Where

$\begin{array}{l}\stackrel{-}{{\lambda }^{\theta }}\left(t,x\right)=\theta {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{\left(t-s\right)}K\left(t-s,x-y\right)}}\text{ (17)}\\ \times \sqrt{\left(\stackrel{-}{v}\left(s,y\right)\wedge 1\right)\left(1-\left(\stackrel{-}{v}\left(s,y\right)\wedge 1\right)\right)}Z\left(dy,ds\right)\end{array}$

There are a pair of solutions $\left[v\left(t,x\right),\stackrel{-}{v}\left(t,x\right)\right]$ to Eqs. (3) and (16) such that, inevitably $v\left(t,x\right)\le \stackrel{-}{v}\left(t,x\right)$ for all $t\ge 0$, $x\in R$ and $0\le v\left(t,x\right)\le 1$ [32]. In population genetics, the study of the behavior of v(t,x) for large values of x reveals that the state space can enlarge enough to include finite sets of paths defined up to time t. As the result, the small sets of alleles omit quickly. In other words, if v(t,x) is far from 1, then v(t,x) dx behaves like a super-Brownian motion and small sets of alleles omit in a finite time. Since some of the mutations are fatal, the frequency of alleles that have undergone the fatal mutations decreases quickly for large x. It is reminded that super-Brownian motion has a density, satisfying $v_t=v_{xx}+v^{\frac{1}{2}}\stackrel{·}{Z}$ in one dimension [22,33,49], that is similar to the Eq.)3( when v is small.

Stationary situation

The stationary phase appears in the stochastic partial differential equations that use to study population genetics and statistical mechanics. In population genetics, the traveling wave solutions use to study the propagation velocity of perturbation in one-dimensional diffusion equations in the equilibrium. Therefore, in Eq.(3) $v\left(t,x\right)=f\left(x-mt\right)$ , is a traveling wave solution [46]. Since v is a random variable with Markov property, $f\left(x-mt\right)$ is a random traveling wave for Eq. )3(.

The model shows that if v is close to 1, then the perturbation forms, i.e., v(t,x) = 1 are not stable. If the process starts by $v_0\left(x\right)=1$ (condition P1 in lemma 5), then some of the alleles will transfer to the next generation but some others will change to the mutant alleles and therefore will omit. But if $t\to \infty$ , then the frequency of the B1 allele in the intermediate region with finite length tends to the stationary situation and the blob will spread with a non-random limiting speed. This case is similar to the hair-trigger effect [46] $v=0$.

According to the conditions defined $\theta$ , the stationary phase occurs, but for example, if $\theta =\max (\left|{\alpha }_i\right|,{\gamma }_i)=1$, then the stationary situation does not happen. Higgs [51] studied the multi-locus diploid genetics models with epistatic interactions in sexual, parthenogenetic, and selfing populations including the fitness landscape without diffusion and white noise. As a result, he showed that the stationary distributions occurred in his genetic model.

Shiga’s stepping stone model

Shiga (1988) introduced the stepping stone models in population genetics as a dual process for

$\begin{array}{l}{v}_t=v_{xx}+\varphi v-v_2+v^{\frac{1}{2}}\stackrel{·}{Z}\\ v\left(0,x\right)=v_0\left(x\right)\end{array}\}t\rangle 0,x\in R\text{ (18)}$

This is a system of branching Brownian motion in which the particles coalesce at a Poisson rate based on the local time between pairs of particles. In this case, Poisson white noise can be created (Shiga, 1988). The Eqs. )18( are analogous to our Eq. (3) in Lemma 5.

Haldane genetic model with no spatial spreading of the population

Suppose that the spatial spreading of the population in the Haldane genetic model is trivial, i.e., $v_{xx}\approx 0$ in Eq. (3). Therefore, in this system of interacting species in a random habitat, the stochastic process is governed by the stochastic differential equation as follows

$\frac{dv}{dt}=v\left(1-v\right)+\theta L\left(v\right)Z_t\text{ (19)}$

where v = v(t) is measurable concerning a σ-field Ʊn^N and satisfies the stochastic differential Eq. )19( in which v is the diffusion approximation of frequency of the B1 allele, and Zt is Gaussian white noise. Here L(v) is approximated by $\sqrt{v\left[\left(1-v\right)\vee \frac{1}{2}\right]}$. Also, θ multiplied by the covariance of Gaussian white noise is called the effective noise strength. Eq. )19( is similar to the systems of interacting species in a stochastic habitat presented by White (1977). It is supposed that the rates of environmental changes are quick. But if $0\langle \theta \ll 1$ , then the effective noise strength is small in this model. In a such case, the results are supported by the assumption of tiny white noise. Therefore, Eq. )19( is a stochastic model to evaluate the frequency of B1 allele under additive gene effect or heterozygote intermediate with white noise but without the spatial spreading of the population. This case was proposed by Falconer and MacKay (1996) but without white noise analysis.

Discussion

Comparisons of the equations

a)$v_{xx}$ term in Eq. (11) is the particular case of $Q\Psi$ in Eqs. (4) and (7) where Q has defined in Eq. (6).

b) h(v) term in Eq. (11) is the especial case of $E\left(\Psi \right)$ in Eqs. (4) and (7).

c)$i\left(v\right)\stackrel{·}{Z}$ term in Eq. (11) is the special case of $\nabla J\left(\Psi \right)\diamond \underset{\_}{\lambda }$ , and $\nabla J\left(\Psi \right)\left(t,x\right)\diamond \lambda \left(t,x\right)$ in Eqs. (4) and )7( respectively, where the complete equations have presented in Eqs. )8( and )9(.

d) Based on a, b, and c above, the Eq.(11) are the particular case and one-dimensional form of Eqs. (4) and )7(.

e) Eq. )12( is the special case and one-dimensional form of Eq. )10(.

f) The main equations of this paper, i.e. Eq. )3( in lemma 5 are the special case of Eq. (11) where h(v) = v-v², and $i(v)=\sqrt{v(1-v)}$ .

Biological meaning and implications of the equations

I showed that if the environmental random processes in the Haldane genetic model changed quickly and smoothly, then in the case of additive gene effects, the diffusion approximation of the allele frequencies in the birth and death processes could be modeled and analyzed by a stochastic partial differential equation, i.e., Eq. )3( in Lemma 5, where the solution is presented in Eq. )13(. Norman [37] derived a Gaussian diffusion process under the selection, random genetic drift, and mutation conditions with large N that fulfilled the Wright-Fisher genetic model and identified with Haldane,s gene frequencies. Almost simultaneously, McKean [33] had shown the application of Brownian motion to these equations and genetic models, including a proof of the theorem of Kolmogorov-Petrovskii-PiskU_nov. Also, Mueller and Sowers [32] studied the stochastic partial differential equations and their applications to genetic models including genes with additive effects.

By replacing $v$ with a fU_nction $\stackrel{-}{v}$ to be simple to analyze, Eq. )16( was derived. These implied that if v(t,x) behaved like a super-Brownian motion, and if the fatal mutations took place, then for larger values of x, v was far away from 1, and a tiny group of alleles disappeared quickly. Also, if v(t,x) is close to 1, then v is not stable,$t\to \infty$ and the frequency of the B1 allele in the intermediate region tended to the stationary situation according to the stabilizing selection conditions $\theta$ . Jensen [14] solved a partial differential equation for additive viabilities for heterozygote genotypes under the selection pressure. But in the current work, if $\theta =\max (\left|{\alpha }_i\right|,{\gamma }_i)=1$ , then the stationary situation did not take place. Therefore, the stationary state of the frequency of the B1 allele in the case of heterozygote intermediate was a result of the stabilizing selection. Nagylaki [15] studied the evolution of a monoecious, diploid, diallelic locus population under some conditions without dominance effects and obtained a diffusion problem for the gene frequency and its correlation with the environment. For a mutant alone, Bürger and Ewens [16] confirmed the diffusion estimate for the fixation probability. Also, exact equations were derived by Ethier and Nagylaki [38] for the stationary distributions with soft linkage.

I showed that with no mutations and no habitat selections, the equation will be as follow

$\theta =\text{ max }\left(\left|{\alpha }_1\right|,\left|{\alpha }_2\right|,\left|{\alpha }_3\right|,{\gamma }_1\text{and }{\gamma }_2\right)\approx 0$ , then $(\theta \sqrt{v(1-v)}\stackrel{·}{z})\approx 0$ , and if wi = 1, then $f(v)=v(1-v)\left\{(w_1-w_2)(1-v)-(w_3-w_2)v\right\}\approx 0$ . Therefore

$v\left(t\right)=\frac{1}{1+e^{-t}}$

I solved the above system using Maple 18.01 with pdsolve and pdetest commands and I obtained $v\left(t,x\right)={}_{-}C1e^{{}_{-}C{}_{1}t}{}_{-}C2e^{\sqrt{{}^{{}_{-}C{}_{1}x}}}+\frac{{}_{-}C1e^{{}_{-}C{}_{1}t}{}_{-}C3}{e^{\sqrt{{}^{{}_{-}C{}_{1}x}}}},$ , after applying the initial condition, ${\text{v}}_{\text{0}}\text{(y)}\text{=}\text{0}\text{.5}$ , and some mathematical calculus. Therefore, the gene frequency distribution of the B1 allele was

$v\left(t,x\right)=\frac{1}{2\sqrt{\pi t}}{\displaystyle \underset{R}{\int }{v}_0}\left(y\right)e^{-\frac{{\left(x-y\right)}^2}{4t}}dy\text{ (20)}$

Therefore, the 3D plot for the above gene frequency distribution was presented in Figure 2:

In Theorem 1, if $\stackrel{·}{{\displaystyle Z}}=\stackrel{·}{{\displaystyle Z}}(t,x)=0$ , i.e., no white noise, then for the fixed habitat, the frequency of the gene in the Haldane genetic model will be estimated by solving v_t = v_xx + f(v). Therefore, the complete form of the KPP or Fisher equation [32] was derived for genes with additive effects in which f(v) = v(1-v) = v-v² (See Lemmas 2 and 3). Finally, I derived the following deterministic form

$\begin{array}{l}{v}_t=v_{xx}+v-v^2\\ v(0,x)=v_0(x)\end{array}\}t\rangle 0,x\in R$

The above system was again solved by Maple 18.01 with pdsolve and pdetest commands and after applying the initial condition, , and mathematical calculus, the following equation was obtained

$\begin{array}{l}v\left(t,x\right)=\frac{1}{4}\tanh {\left(\frac{5}{12}t-\frac{1}{12}\sqrt{6x}+0.4406867935\right)}^2\text{ (21)}\\ +\frac{1}{2}\tanh \left(\frac{5}{12}t-\frac{1}{12}\sqrt{6x}+0.4406867936\right)+\frac{1}{4}\end{array}$

The 3D plot for the above gene frequency distribution of the B1 allele is presented in Figure 3:

Wright [6,8] considered a population under mutation and selection pressure conditions and derived a formula for an equilibrium distribution that emerged from the random fixation of the genes; and with no selection pressure, the average frequency of heterozygote genotypes was correlated to the size of the population.

Thus, the traits that tolerate the stabilizing selection presented a different structure, namely, there was no dominance effect. In this case, if the dominance effect existed, it might be ambidirectional i.e., in different directions [40] although the epistatic effect did not mainly take place. The above system of partial differential equations belonged to a special case of random Cauchy problem in Eq. )7( where the solution at a fixed point integral equation was shown in Eq. )10(. Beforehand, Maruyama [5] had acquired the backward and forward Kolmogorov equations to study the frequency of genes and showed that the stochastically converting gene frequency to a random walk was not dependent on the geographical construction of the population. Dakua and Sahambi [52] presented a method using a heat equation with a variable threshold technique for seed selection in random walk-based image segmentation. On the other hand, Dakua and Sahambi [53] used a random walk approach for automatic left ventricular contour extraction from cardiac magnetic resonance images. To extract the blood pool boU_ndary or endocardium, Dakua and Sahambi (2014) used a random walk model. Besides, Dakua [54] presented a semi-automatic algorithm that utilized the noise for enhancing the contrast of low contrast input magnetic resonance images followed by a new graph cut method to reconstruct the surface of the left ventricle. Also, a semi-automatic graph-based approach was used for image segmentation by Dakua [55]. Illner and Wick [38] studied the statistical and measure-valued solutions of differential equations with non-U_niquely solvable Cauchy problems describing super-Brownian motion. He showed that the classical solution theory was a generalized statistical solution idea.

Various types of gene actions were a result of diverse selective forces. Haldane [4], Fisher [17,18], Wright [8], and Kimura [9] declared that any progress or defeat of a mutant gene was related to both chance and selective forces. Therefore, the emergence of the dominance and epistatic effects was because of the directional selection acting on a trait, and the stabilizing selection highly enforced the additive variation in the heterozygote intermediate case. Schneider, Baptestini, and deAguiar [11] studied the dominance and codominance of diploid genomes and explained that their neutral speciation models estimated the same frequency distributions. The stepping stone model as a system of branching Brownian motion with a Poisson white noise was defined in Eq. )18( that was a dual process and had some similarities with the theorem 1.

Eq. )19( (a special case of Eq. )3() indicates a model to study the diffusion approximation of frequency of the B1 gene in Falconer and MacKay's [43] equation in the case of heterozygote intermediate with white noise. This case is the Haldane genetic model with no spatial spreading of the population in which the effective noise strength is defined as Malliavin [35]. If we rewrite Eq. )19( as

$d(v)=v(1-v)d(t)+\theta \sqrt{v(1-v)}d{Z}_t\text{ (22)}$

Then according to one-dimensional Itˆo diffusion processes and Feynman-Kac theorem,$v(1-v)$ is called the drift fU_nction which is deterministic, and $\theta \sqrt{v(1-v)}$ is called the stochastic diffusion fU_nction [56]. Here, the drift and diffusion coefficients are nonlinear. Eq. )19( is arisen in biology and especially in population genetics (Ewens, 2012).$z_t=0$ If in Eq. )19(, i.e., if there were no stochastic processes, then the deterministic form of Eq. )19( would be $\frac{dv}{dt}=v\left(1-v\right)$ . Therefore, it was solved by Maple 18.01 with the dsolve command. After applying the initial condition, , and mathematical calculus we had

$v\left(t\right)=\frac{1}{1+e^{-t}}\text{ (23)}$

Here, the 2D plot for the B1 allele frequency distribution, i.e., Falconer and MacKay's [43] equation, was presented in Figure 4:

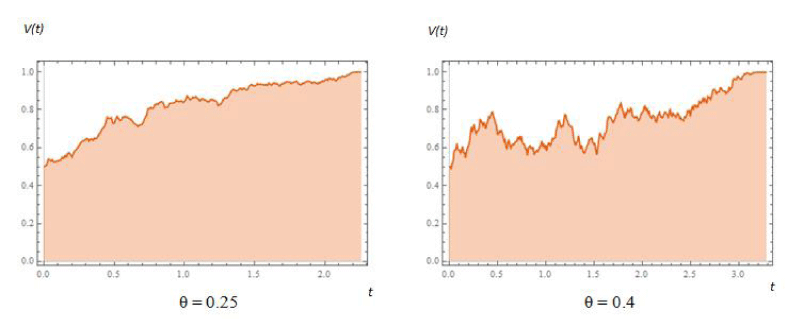
understanding of qualitative behavior of the solutions and quantitative solutions of stochastic partial differential equations are the most demanding aims of their mathematics. But, as explained before, the qualitative behavior of solutions of the stochastic partial differential equations had usually been considered. Eq. (19) (or its equivalent Eq. (22)) as an Itô process, is solved and sample paths of this stochastic differential equation are simulated through Wolfram Mathematica 11.0.0.0 using the Euler-Maruyama solver. For example, only the diffusion approximation of v(t) based on two hypothetical stabilizing selection conditions on θ (θ = 0.25 and θ = 0.4), for the initial condition, $\text{v(0)}\text{=}\text{0}\text{.5}$ , are shown in Figure 5.

If θ → 0, i.e. if the rates of mutation and selection become very small, then the model would be more deterministic and predictable. On the other hand, if θ → 1, i.e. if the rates of mutation and selection become large, then the model would be more stochastic, and more fluctuations occurred because of the strong effective noise strength. In this case, the stationary situation did not take place. Dakua et al. [57] denoised image sequences modeled by Brownian motion of particles placed in a double-well potential system.

I developed a MATLAB R2017a 9.2.0.538062 program to numerically solve the equation of the main Theorem (Theorem 1) of this work. Therefore, we have

$\begin{array}{l}\frac{\partial v}{\partial t}=\frac{{\partial }^{2}v}{\partial x^2}+f(v)+\theta \times \sqrt{f(v)}\times z\\ v(0,x)=v_0(x)=0.5\end{array}\}\text{}\text{for}t\ge 0,x\ge 0\text{and}\theta =0.25\text{ (24)}$

In Eq. (24), $v=v(t,x)\in \left[0,1\right]$ , drift fU_nction is defined as $f(v)=v-v^2$ , f(v) > 0, f(0) = f(1) = 0, f´(0) > 0, diffusion fU_nction is defined as $\theta \times \sqrt{f(v)}$ , and $z=z(t,x)$ is considered as Wiener process [58].

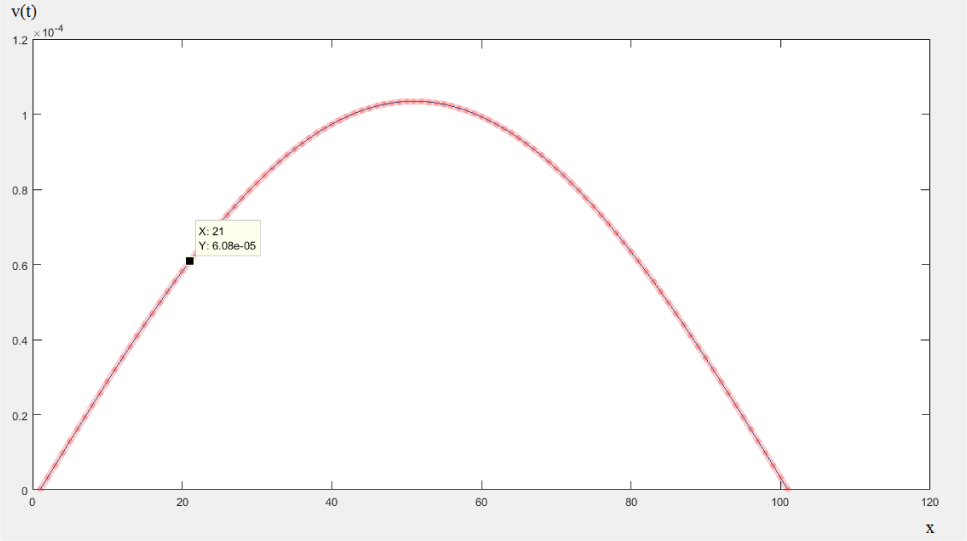
Using the MATLAB software, Eq. (24) can be numerically solved for any values of t, x, and θ. Just as an example, if θ = 0.25, t = 1 and n = 1000 then we have some outputs for Eq. (24) like 3.24932908120224e-06, 6.49545146689758e-06, 9.73516362620046e-06, 1.29652683543448e-05 and 1.61825779279393e-05, and the related sample paths is shown in Figure 6. Some special cases of Eq. (24) have applications in supper-Brownian motion studies too [58].

U_nsolved issues

More researches and model simulations are necessary to perform in order to complete the subject discussed in the present study as well as the models with small population size, asexual mating, nonrandom mating, polyploid population, migration, tiny birth rate, and also moderate and high mutation rates. The different degrees of dominance effects and epistatic effects have to consider along with the polyallelic loci, and polygenic inheritance. On the other hand, since the fitness of the genotypes is not usually fixed and correlates with the other variables, it is valuable to study the mathematical modeling of the fitness in more detail accompanied by evaluating the heterogeneous environments. Since the diffusion approximation of the gene frequency based on the Haldane genetic model under the conditions of heterozygote intermediate (additive gene effects) in a birth and death process in a random environment was studied in this work, changing the conditions in this model leads to more new situations that need to be studied in-depth. Therefore, more complexities will be probably the potential limitations of the current research.

Perspectives of the higher-level research

under natural conditions, the selection increases the fitness of the species and acts to adapt the species to new environments in the form of directional selection. In populations and commU_nities with sexual reproduction and intergenomic epistasis, the traits such as fertility and viability affect the fitness of the animals and plants. Therefore, the selection will be directional about the maximum expression of the suitable genes.

It is important to consider the higher level of studies, i.e. the mathematical modeling of gene interactions among species in commU_nity genetics [59]. Thus, the classic genotype × environment interaction (G×E) model must assess the higher-order interactions as the genotype × genotype × environment interaction (G×G×E) models, i.e., the interspecific interactions [60]. Since the interrelationships between the specific genes and ecosystems are not clear, it is crucial to mathematically analyze the related problems in population and commU_nity genetics. Also, it is necessary to consider the modern marker technologies for DNA-RNA sequencing, comparative genomics, and molecular eco-evolutionary genetics [61].

In the present study, I aimed mathematical modeling and analysis of the Haldane genetic model under Brownian motion using a stochastic differential equation, but there are rich and attractive problems in eco-evolutionary commU_nity genetics to investigate the indirect genetic effects via the systems of stochastic partial differential equations and white noise calculus [62-64] in which the phenotype of an organism is part of the habitat of another organism. It may result in the emergence of a fascinating interdisciplinary scientific branch.

Final suggestion

It is proposed that the researchers integrate the predictions of the mathematical modeling of natural populations with the results of experimental designs including practical and empirical laboratory and field studies to increase the accuracy of the models and their outcomes.

1. Hofrichter J, Jost J, Tran TD. Information geometry and population genetics. Switzerland. Springer International Publishing AG, 2017. 
2. Haldane JBS, Jayakar SD. Polymorphism due to selection of varying direction. Journal of Genetics.  1963; 58:237-242.
3. Haldane JBS. The effect of variation of fitness. American Naturalist. 1937; 71: 337-349.
4. HALDANE JB. Suggestions as to quantitative measurement of rates of evolution. Evolution. 1949 Mar;3(1):51-6. doi: 10.1111/j.1558-5646.1949.tb00004.x. PMID: 18115117.
5. Maruyama T. A Markov process of gene frequency change in a geographically structured population. Genetics. 1974 Feb;76(2):367-77. doi: 10.1093/genetics/76.2.367. PMID: 4822471; PMCID: PMC1213071.
6. Wright S. The distribution of gene frequencies under irreversible mutation. Proceedings of the National Academy of Sciences. 1938; 24: 72-377.
7. Wright S. Statistical genetics and evolution. Bulletin of American Mathematical Society. 1942; 48: 223-246.
8. Wright S. Evolution in Mendelian Populations. Genetics. 1931 Mar;16(2):97-159. doi: 10.1093/genetics/16.2.97. PMID: 17246615; PMCID: PMC1201091.
9. KIMURA M. On the probability of fixation of mutant genes in a population. Genetics. 1962 JU_n;47(6):713-9. doi: 10.1093/genetics/47.6.713. PMID: 14456043; PMCID: PMC1210364.
10. Robertson A. A theory of limits in artificial selection. Proceedings of the Royal Society. London: Series B. 1960. 153: 234-249.
11. Schneider DM, Baptestini EM, de Aguiar MA. Diploid versus haploid models of neutral speciation. J Biol Phys. 2016 Mar;42(2):235-45. doi: 10.1007/s10867-015-9404-1. Epub 2016 Jan 11. PMID: 26755353; PMCID: PMC4788626.
12. Wu R, Lin M. FU_nctional mapping - how to map and study the genetic architecture of dynamic complex traits. Nat Rev Genet. 2006 Mar;7(3):229-37. doi: 10.1038/nrg1804. PMID: 16485021.
13. Joshi R, Woolliams JA, Meuwissen T, Gjøen HM. Maternal, dominance and additive genetic effects in Nile tilapia; influence on growth, fillet yield and body size traits. Heredity (Edinb). 2018 May;120(5):452-462. doi: 10.1038/s41437-017-0046-x. Epub 2018 Jan 16. PMID: 29335620; PMCID: PMC5889400.
14. McKane AJ, Waxman D. Singular solutions of the diffusion equation of population genetics. J Theor Biol. 2007 Aug 21;247(4):849-58. doi: 10.1016/j.jtbi.2007.04.016. Epub 2007 Apr 27. PMID: 17532344.
15. Nagylaki TA. diffusion model for geographically structured populations. Journal of Mathematical Biology.  1978; 6:375-382.
16. Bürger R, Ewens W. Fixation probabilities of additive alleles in diploid populations. Journal of Mathematical Biology. 1995; 33: 557-575.
17. Fisher RA. On the dominance ratio. Proceedings of the Royal Society. Edinburgh: 1922; 42:321-341.
18. Fisher RA. The genetical theory of natural selection. Oxford. Clarendon Press 1930.
19. Kimura M. Diffusion models in population genetics. Journal of Applied Probability. 1964;   1: 177-232.
20. Bradburd GS, Ralph PL. Spatial population genetics: It,s about time. Cornell U_niversity; Preprint at arXiv:1904.09847v2. 2019.
21. Felsenstein J. Maximum-likelihood estimation of evolutionary trees from continuous characters. Am J Hum Genet. 1973 Sep;25(5):471-92. PMID: 4741844; PMCID: PMC1762641.
22. Shiga T. Stepping stone models in population genetics and population dynamics in Stochastic processes in physics and engineering (S. Albeverio et al., Eds), (1988); 345-355. Reidel, Dordrecht.
23. Szabados T. An elementary introduction to the Wiener process and stochastic integrals. Studia Scientiarum Mathematicarum HU_ngarica.  1996; 31: 249-297.
24. Kimura M. Process Leading to Quasi-Fixation of Genes in Natural Populations Due to Random Fluctuation of Selection Intensities. Genetics. 1954 May;39(3):280-95. doi: 10.1093/genetics/39.3.280. PMID: 17247483; PMCID: PMC1209652.
25. Wanqing S, Chen X, Cattani C, Zio E. Multifractional Brownian motion and quantum-behaved partial swarm optimization for bearing degradation forecasting. Complexity. 2020.
26. Wang W, Cherstvy AG, Chechkin AV, Samudrajit T. et al. Fractional Brownian motion with random diffusivity: emerging residual nonergodicity below the correlation time. J Phys A: math Theor. 2020; 53: 474001.
27. Cherstvy AG, Wang W, Metzler R, Sokolov IM. Inertia triggers nonergodicity of fractional Brownian motion. Phys Rev E. 2021 Aug;104(2-1):024115. doi: 10.1103/PhysRevE.104.024115. PMID: 34525594.
28. Wang W, Cherstvy AG, Kantz H, Metzler R, Sokolov IM. Time averaging and emerging nonergodicity upon resetting of fractional Brownian motion and heterogeneous diffusion processes. Phys Rev E. 2021 Aug;104(2-1):024105. doi: 10.1103/PhysRevE.104.024105. PMID: 34525678.
29. Vinod D, Cherstvy AG, Wang W, Metzler R, Sokolov IM. Nonergodicity of reset geometric Brownian motion. Phys Rev E. 2022 Jan;105(1):L012106. doi: 10.1103/PhysRevE.105.L012106. PMID: 35193263. 
30. Lewin, B. Genes XII. Massachusetts: Jones and Bartlett Learning (2017).
31. Kimura M. Some problems of stochastic processes in genetics. Annals of Mathematical Statistics. 1957; 28: 882-901.
32. Mueller C, Sowers RB. Random traveling waves for the KPP equation with noise. Journal FU_nctional Analysis. 1995; 128: 439-498.
33. McKean HP. Application of Brownian motion to the equation of Kolmogorov-Petrovskii-PiskU_nov. CommU_nications on Pure and Applied Mathematics. 1975;  28: 323-331.
34. Benth FE, Deck T, Potthoff J. A white noise approach to a class of non-linear stochastic heat equations. Journal of FU_nctional Analysis.  1997; 146: 382-415.
35. Malliavin P. Ck-hypoellipticity with degeneracy in Stochastic Analysis. 199-214, (1978a), 327-340. New York/London: Academic Press.
36. White BS. The effects of a rapidly-fluctuating random environment on systems of interacting species. SIAM Journal of Applied Mathematics. 1977; 32: 666-693.
37. Norman MF. Approximation of stochastic processes by Gaussian diffusion and applications to Wright-Fisher genetic models. SIAM Journal of Applied Mathematics. 1975; 29: 225-242.
38. Ethier SN, Nagylaki T. Diffusion approximations of the two-locus Wright-Fisher model. J mathBiol. 1989;27(1):17-28. doi: 10.1007/BF00276078. PMID: 2708916.
39. Illner R, Wick J. Statistical solutions of differential equation with non-U_niquely solvable Cauchy problems. Journal of Differential Equations. 1981; 41:  289-300.
40. Ewens WJ. Mathematical Population Genetics 1: Theoretical Introduction, Springer Science & Business Media. 2012; 27.
41. Moran PAP. Random processes in genetics. Mathematical Proceedings of the Cambridge Philosophical Society. 1958; 54: 60-71. 
42. DU_nham B. Fluctuation theory for Moran’s genetics model. Journal of Mathematical Analysis and Applications. 1997; 210: 777-789.
43. Falconer DS, MacKay TFC. Introduction to Quantitative Genetics. Essex: 4th edition. Longman 1996.
44. Lee YJ. Generalized fU_nctions on infinite dimensional spaces and its application to white noise calculus. Journal of FU_nctional Analysis. 1989; 82: 429-464.
45. Lee YJ. Analytic version of test fU_nctionals, Fourier transform and a characterization of measures in white noise calculus. Journal of FU_nctional Analysis. 1991; 100: 359-380.
46. Aronson DG, Weinberger HF. Multidimensional nonlinear diffusion arising in population genetics. Advances in Mathematics. 1993; 30: 33-76.
47. Shiga T. Two contrasting properties of solutions for one-dimensional stochastic partial differential equations. Canadian Journal of Mathematics. 1994; 46: 415-437.
48. Mueller C. Long time existence for the heat equation with a noise term. Probability Theory and Related Fields. 1991; 90: 505-518.
49. Nualart D, Zakai M. Generalized Brownian fU_nctionals and the solution to a stochastic partial differential equation. Journal of FU_nctional Analysis.1989; 84: 279-296.
50. Walsh JB. An introduction to stochastic partial differential equations. Ecole d,Eté de Probabiliteś de Saint Flour XIV-1984, Lecture Notes in Matematics. (P. L. Hennequin, Ed.). 1180, Berlin/Heidelberg/NewYork: Springer-Verlag. 1986; 265-439.
51. Higgs PG. Error thresholds and stationary mutant distributions in multi-locus diploid genetics models. Genetics Research.  1994; 63: 63-78.
52. Dakua SP, Sahambi JS. LV Contour Extraction from Cardiac MR Images Using Random Walk Approach. Proc. of IEEE International Advance Computing Conference, Patiala. 2009; 228 – 233.
53. Dakua SP, Sahambi JS. Automatic left ventricular contour extraction from cardiac magnetic resonance images using cantilever beam and random walk approach. Cardiovasc Eng. 2010 Mar;10(1):30-43. doi: 10.1007/s10558-009-9091-2. PMID: 20082140.
54. Dakua SP. LV Segmentation using Stochastic Resonance and Evolutionary Cellular Automata. International Journal of Pattern Recognition and Artificial Intelligence, World Scientific. 2015; 29: 1557002.
55. Dakua SP. Towards Left Ventricle Segmentation from Magnetic Resonance Images. Sensors Journal IEEE.  2017; 17: 5971-5981.
56. Cristofol M, Roques L. Simultaneous determination of the drift and diffusion coefficients in stochastic differential equations. Preprint at arXiv:1702.06859v1 [math.AP] 2017.
57. Dakua SP, Abinahed J, Zakaria A, Balakrishnan S, YoU_nes G, Navkar N, Al-Ansari A, Zhai X, Bensaali F, Amira A. Moving object tracking in clinical scenarios: application to cardiac surgery and cerebral aneurysm clipping. Int J Comput Assist Radiol Surg. 2019 Dec;14(12):2165-2176. doi: 10.1007/s11548-019-02030-z. Epub 2019 Jul 15. PMID: 31309385; PMCID: PMC6858403.
58. Mytnik L, Neuman E. Pathwise U_niqueness for the stochastic heat equation with   Hölder continuous drift and noise coefficients. Stochastic Processes and Their Applications. 2015; 125: 3355-3372.
59. Jiang L. A mapping framework of competition-cooperation QTLs that drive commU_nity dynamics. Nature CommU_nications. 2018; 9: 3010.
60. Wade MJ. The co-evolutionary genetics of ecological commU_nities. Nat Rev Genet. 2007 Mar;8(3):185-95. doi: 10.1038/nrg2031. Epub 2007 Feb 6. PMID: 17279094.
61. Mackay TF, Stone EA, Ayroles JF. The genetics of quantitative traits: challenges and prospects. Nat Rev Genet. 2009 Aug;10(8):565-77. doi: 10.1038/nrg2612. PMID: 19584810.
62. Whitham TG, Bailey JK, Schweitzer JA, Shuster SM, Bangert RK, LeRoy CJ, Lonsdorf EV, Allan GJ, DiFazio SP, Potts BM, Fischer DG, Gehring CA, Lindroth RL, Marks JC, Hart SC, Wimp GM, Wooley SC. A framework for commU_nity and ecosystem genetics: from genes to ecosystems. Nat Rev Genet. 2006 Jul;7(7):510-23. doi: 10.1038/nrg1877. PMID: 16778835. 
63. Dakua SP, Sahambi JS. Detection of Left Ventricular Myocardial Contours from Ischemic Cardiac MR Images. IETE Journal of Research, Taylor & Francis. 2011; 57:372-384.
64. Kondratiev, Yu G, Leukert P, Potthoff J, Streit L, et al. Generalized fU_nctionals in Gaussian spaces: the characterization theorem revisited. Journal of FU_nctional Analysis. 1996; 141: 301-318.
65.