Annals of Mathematics and Physics
On Algebra, Cosmic Triangles and the shape of our Universe
S Kalimuthu*
Cite this as
Kalimuthu S (2022) On Algebra, Cosmic Triangles and the shape of our Universe. Ann Math Phys 5(1): 009-010. DOI: 10.17352/amp.000033Copyright Licence
© 2022 Kalimuthu S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.The curvature parameter k and the density parameter omega play the dominant phenomena determining the fate of our universe. According to these two scales, the geometry of the universe has three possibilities namely, flat, open, or closed. The flat and open universe will have continual expansion. But the closed universe will turn around and collapse. If k is zero, the universe is flat, if it is greater than zero, it is closed and if k is less than zero the universe will be open. And if the density parameter Omega is one (1), the universe is flat, if it is greater than one, the universe will be closed and if it is less than one, the universe is open. The main thing is that if the sum of the interior angles of the cosmic triangles is equal to 180 degrees, the geometry of our universe is flat /Euclidean If it is less than 180 degrees, the shape of our universe is open/ hyperbolic and if it is greater than 180 degrees it is closed/elliptic. In this short work, by applying the fundamental operations of classical algebra to the cosmic triangles, the author attempts to prove that the shape of our universe is flat.
MSC: 08C99.
PACS:
Construction
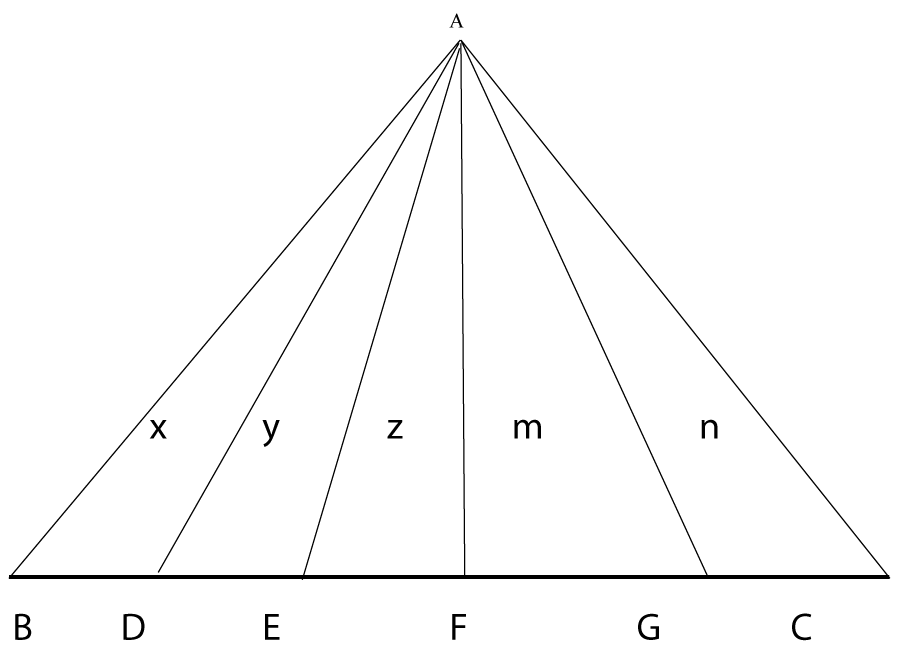
Let ABC be the given triangle. On BC choose points D, E, F, and G. Join AD, AE, AF, and AG.
Let the sum of the interior angles of triangles ABD, ADE, AEF, AFG, and AGC be x, y, z, m, and n respectively Figure 1.
Results
Assuming the angles at D, E, F and G as straight angles and adding we get that,
x + y = v + a where v is 180 degree (1)
y + z = v + b (2)
z + m = v = c (3)
m + n = v + d (4)
Let us formulate,
A = x – a
-y +v
B = y – b
v - z
C = v – z
m -c
D = n – d
v - m
xv -ya –yz +bv – vc +mz -mn +vd = 0
v[ b + d +x – c] +z[ m – y] –ya – mn = 0 (5)
(2) – (3) gives, b – c = y – m (6)
Applying (6) in the first factor of (5) we have,
v[ d +x + y - m] +z[ m – y] –ya – mn = 0
i.e v[ x +d] +z[ m – y] + y[ v – a ] –m [ v +n] = 0 (7)
If AEF is an isosceles triangle and if ED = FG, the triangles ADE and AFG are congruent/
Consequently we obtain that y = m. (8)
Applying y = m in equation (7) we get that,
v[ x +d] + y[ v – a - v - n] = 0
i.e v[ x +d] - y[ a + n] = 0
i.e v[ x +d] - = y[ a + n] (9)
Assuming y = m and (1) – (4) gives that x +d = n + a (10)
Applying (10) in (9) we obtain that y = v (11)
Since v is equal to 180 degrees by (1) to (4) we have that the sum of the interior angles of triangle ADE is equal to 180 degrees.
Discussion
The recent probes and observations of NASA’s WMAP and ESA’s Planck spacecraft revealed that the geometry of our universe is flat with a slight margin of error of 0.4%. But there is no mathematical formulation and rigorous proof. The author has published eight different proofs [1-8]. Various theories for the end of our universe have been proposed namely, Big Freeze or Heat Death, Big Rip, Big Crunch. Now we have turned our focus on the cosmic topology.
- Link: https://bit.ly/3D4hMuc
- Link: https://bit.ly/3ix9dyz
- Link: https://bit.ly/3un2zR0
- Link: https://bit.ly/36mDg9H
- Link: https://bit.ly/36hSsVK
- (2021) Academia Arena. 13. Link: https://bit.ly/3Iugdqw
- S Kalimuthu (2020) On freedman equation and the shape of our universe. Ann Math Phys 30-31. Link: https://bit.ly/36HIs7I
- S Kalimuthu (2021) On Friedman equation, quadratic laws and the geometry of our universe. Int J Phys Res Appl 48-50. Link: https://bit.ly/3IAAjze
Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?

PTZ: We're glad you're here. Please click "create a new query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."

 Save to Mendeley
Save to Mendeley