Time series analysis of Holt model and the ARIMA Model facing Covid-19

Background: Since the first appearance of the novel coronavirus in Wuhan in December 2019, it has quickly swept the world and become a major security incident facing humanity today. While the novel coronavirus threatens people’s lives and safety, the economies of various countries have also been severely damaged. Due to the epidemic, a large number of enterprises have faced closures, employment has become more difficult, and people’s lives have been greatly affected. Therefore, to establish a time series model for Hubei Province, where the novel coronavirus first broke out, and the United States, where the epidemic is most severe, to analyze the spreading trend and short-term forecast of the new coronavirus, which will help countries better understand the development trend of the epidemic and make more adequate preparation and timely intervention and treatment to prevent the further spread of the virus.

Methods: For the data collected from Hubei Province, including cumulative diagnoses, cumulative deaths, and cumulative cures, we use SPSS to establish the time series model. Since there is no problem of missing data values, we define days as the time variable, remove outliers, and set the width of the confidence interval to 95% for prediction, then use SPSS’s expert modeler to find the best-fit model for each sequence. ACF, PACF graphs of the residuals, and Q-tests are used to determine whether the residuals are white noise sequences and to check whether the model is a suitable model. Holt model is used for the cumulative number of diagnoses, and ARIMA (1,2,0) model is used for cumulative cures and deaths. Similarly, we also collect data for the US, including the cumulative number of diagnoses, cumulative deaths, and cumulative cures. For the three groups mentioned above, ARIMA (2,2,6) model, ARIMA (0,2,0) model, and ARIMA (0,2,1) model are used respectively.

Findings: From our modeling of the data, the time series diagrams of the real the fitted data almost overlap, so the fitting effect of the Holt model and the ARIMA model we use is very suitable. We compare the predicted values with the real values of the same period and find that the epidemic situation in Hubei Province has basically ended after May, but the epidemic situation in the United States has become more severe after May, so the Holt model and the ARIMA model are also very appropriate in predicting the epidemic situation in short-term.

Interpretation: Because the Chinese government has always put the safety of people ’s lives in the first place, when the epidemic broke out, it decisively closed the city of Hubei Province. One side is in trouble, all sides support, they concentrate all resources of whole country to save Hubei Province at the expense of the economy only in order to save more people. Now we can clearly see that the epidemic has been controlled in China and the whole country is developing in a good direction. The situation in the United States, on the other hand, is also influenced by the social environment.

Introduction

Since December 2019, many cases of cough, dyspnea, fatigue and fever have been reported in Wuhan, China, in a short period of time. Unexplained cases of pneumonia with major symptoms. The Chinese health authorities and the Centre for Disease Control and Prevention (CDC) promptly identified the causative agent of these cases as a novel coronavirus, and the World Health Organization (WHO) in November 2009 identified the virus as the main cause of pneumonia. On January 10, 2020, it was named COVID-19. on January 22, 2020, the People’s Republic of China the State Council Information Office held a press conference on pneumonia to prevent and control neo-coronavirus infections. On the same day, the Center for Disease Control and Prevention of the People’s Republic of China released a plan for the prevention and control of neo-coronavirus infection of pneumonia. Includes COVID-19 epidemiological study, specimen collection and testing, follow-up and management of close contacts and information, education and training. Risk communication with the public.

And now in May in our country is almost under control, but in the meantime the novel coronavirus has brought the life of the people and the development of the national economy. Coronaviruses are a large family of viruses that are known to cause influenza as well as Middle East Respiratory Syndrome (MERS) and Severe Acute Respiratory Syndrome (SARS). Coronaviruses are a large family of viruses known to cause influenza, as well as Middle East Respiratory Syndrome (MERS) and Severe Acute Respiratory Syndrome (SARS). More Serious diseases such as respiratory syndrome (SARS). Novel coronaviruses are new strains of coronaviruses that have never been found in humans before. Common signs of coronavirus infection in humans include respiratory symptoms, fever, cough, shortness of breath, and difficulty breathing. In more severe cases, the infection can lead to pneumonia, severe acute respiratory syndrome, kidney failure, and even death. Not only that, but in later cases we also found a proportion of asymptomatic infections, which is defined as the absence of relevant clinical symptoms (e.g., self-perceived or clinically recognizable symptoms and signs such as fever, cough, sore throat, etc.), respiratory and other specimens of coronavirus etiology (usually referred to as a nucleic acid test) or a positive serum-specific Immunoglobulin M (IgM) antibody test. An asymptomatic infected person is not a confirmed case and therefore is not counted as a newly infected patient. announced by the NCHS on March 4, 2020. This provision was not changed in the seventh edition. Asymptomatic infected persons actually comprise two segments of the population: the first is those who are insidiously infected, with no or very mild symptoms. The other part of the population is in a latent phase after infection and may develop symptoms in the future.

Asymptomatic infections can be divided into two scenarios: first, an infected person tests positive for nucleic acid, and after a 14-day incubation period, none of them have any Self-perceptible or clinically recognizable signs and symptoms, always in an asymptomatic state of infection; secondly, positive nucleic acid tests in infected persons. The absence of any self-perceived or clinically recognizable signs and symptoms at the time of sampling, but the subsequent appearance of some clinical manifestation, i.e., latent “Asymptomatic infection” status. Unfortunately, there is currently no specific treatment for diseases caused by novel coronaviruses. However, many of the symptoms can be managed and therefore need to be treated according to the patient’s clinical condition. In addition, supportive care for infected patients may be very effective.

By establishing COVID-19 spread models between China and the United States, we can clearly see the different results of different policies and measures on the control of the epidemic. This is also the significance of our model. Through accurate data and rational analysis, we can provide the future development trend and control strategy research for the world in the fight against the epidemic [1,2].

Methods

Data

The data of Hubei Province is derived from the Health Commission of Hubei Province on its official platform from 20 January, 2020. The Hubei Province data collected in this paper includes cumulative deaths, cumulative cures and cumulative diagnoses from 20 January, 2020 to 28 April, 2020 [3].

The data of the United States comes from the domestic data platform, the Real-time Big Data Report of the Epidemic. The data collected in this paper includes cumulative deaths, cumulative cures and cumulative number of diagnoses from 29 February, 2020 to 28 April, 2020 [4].

The model

Through the collected data, we conduct a time series analysis of the novel coronavirus [5-7]. Because there is no data missing, we import the data into SPSS, define the day as the time variable, remove the outliers, and make time series graphs. The most suitable fitting models are automatically found by the expert modeler, which include the cumulative deaths, cumulative cures and cumulative diagnoses. The explanation of abbreviations used in time series analysis are listed below.

As the Table 1 shows, the ACF and the PACF are used to check whether the model is fitted. The ACF is the autocorrelation coefficient and does not control for other variables. The partial autocorrelation coefficient PACF, on the other hand, is the autocorrelation coefficient calculated after controlling for other variables, since it hacks out the effects of other variables. ACF is mainly used for MA model, and PACF is mainly used for AR model. The Table 2 listed below illustrates the meaning of ACF and PACF plots in AR model, MA model, ARMA model.

TS Model-based method for estimation in hubei province

Based on the given data of cumulative number of diagnoses in Hubei Province, we use the expert modeler to process the data and obtain the Holt model [8,9], to describe it. The corresponding equation set shown below.

$$\left\{\begin{array}{l}{S}_t=\alpha X_{t+}(1-\alpha )(S_{t-1}+T_{t-1}\\ T_t=\beta (S_t-S_{t-1})+(1-\beta )T_{t-1}\\ \stackrel{⌢}{\text{X}}{\text{(m)=S}}_{\text{t}}{\text{+mT}}_{\text{t}}\end{array}\right\}$$

The related mathematical symbols used above are listed in the following Table 3.

Table 3: Mathematical symbols used in equation set .
Symbols	Meanings for each symbol
t	Current period
Xt	Actual observations in period t
St	Estimated level at period t
Tt	Predicted trend at period t
	Estimated value before period m
	Horizontal smoothing parameter
	Trend smoothing parameter
m	The number of periods ahead of the forecast, i.e., the forecast step size

Finally, we find that α=1, β=0.1.

In order to determine that the selected Holt model can correctly describe the cumulative number of diagnoses, we use white noise [10], for residual test.

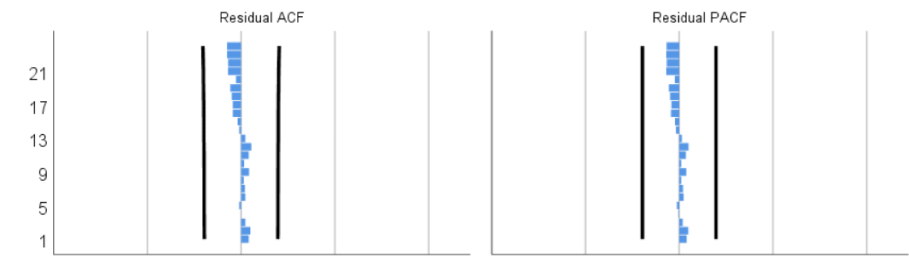
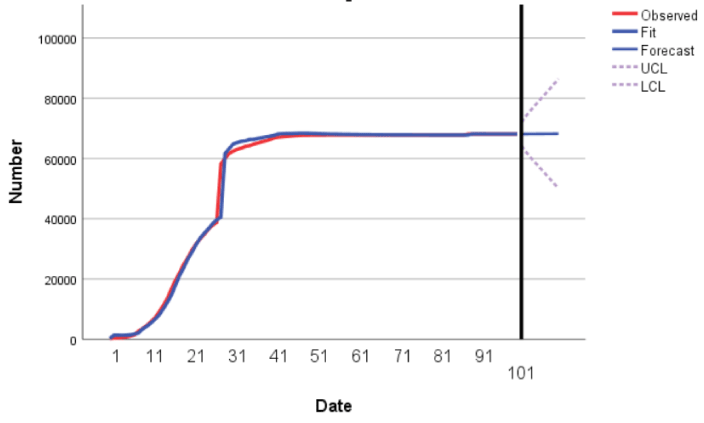
From Figure 1, the ACF and PACF graphs of the residuals can be seen that the autocorrelation coefficients and partial correlation coefficients of all lag orders are not significantly different from 0.From Figure 2, it can also be seen that the P value obtained by the Q test is 1, that is, we cannot reject the null hypothesis and think that the residual is a white noise sequence, so the Holt model can describe the cumulative number of diagnoses well.

Figure 1: The ACF and PACF graphs of the residuals in cumulative number of diagnoses in Hubei Province case.

Figure 2: The Q test on the residual of the case of cumulative number of diagnoses in Hubei Province case.

From the analysis above, we can conclude that the Holt model can describe the cumulative number of diagnoses well.

Similarly, the expert modeler evaluates that the cumulative number of cures conforms the ARIMA (1, 2, 0) model [11]. The related equations are demonstrated followed.

$$(1-{\displaystyle {\sum }_{i=1}^p}{\alpha }_i{L}^i){(1-L)}^d{y}_t={\alpha }_0+(1+{\displaystyle {\sum }_{i=1}^q}{\beta }_i{L}^i){\epsilon }_t$$

The related mathematical symbols used above are listed in the following Table 4.

Table 4: Mathematical symbols used in equations ,.
Symbols	Meanings for each symbol
p	Number of autoregressive items
q	Moving average number of items
d	The number of differential steps made to become a smooth sequence
L	Lag operator
	AR(p) model
	MA(q) model
	2nd order difference
	Number of people on day t
	Coefficients of the i-th order lagged term in the AR(p) model
	Coefficients of the i-th order lagged term in the MA(q) model

The lag operator used in equation , indicates the difference. The Table 5 below shows the specific functions of lag operator.

Table 5: Functions of lag operator.
Functions	Corresponding equations
d-order differential
Seasonal difference (m for period)

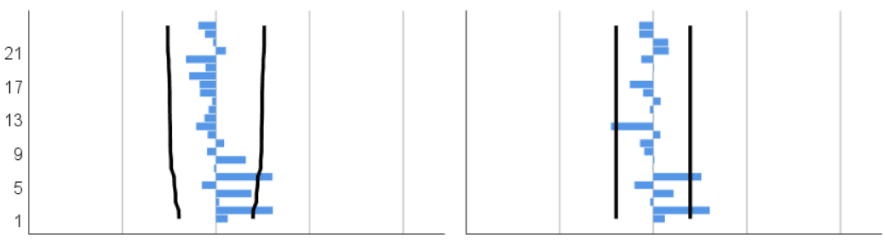
We also use white noise to test this model for residuals. As Figure 3 below shows, the ACF and PACF graphs of the residuals can be seen that the autocorrelation coefficients and partial correlation coefficients of all lag orders are not significantly different from 0. Therefore, the ARIMA (1, 2, 0) model can well describe the cumulative number of cured people.

Figure 3: The ACF and PACF graphs of the residuals in cumulative number of cures in Hubei Province case.

Similar to the cumulative number of people cured in Hubei Province, the cumulative number of deaths in Hubei Province also conforms to the ARIMA (1, 2, 0) model. The corresponding equation and the related symbol meanings are the same as equation .

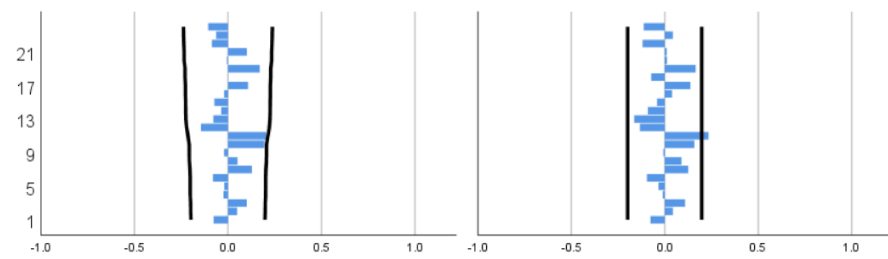
Next, we use white noise for the residual test. From Figure 4, the ACF and PACF graphs of the residuals can be seen that the autocorrelation coefficients and partial correlation coefficients of all lag orders are not significantly different from 0. we can find that the ARIMA (1, 2, 0) model can also describe the cumulative death toll well.

Figure 4: The ACF and PACF graphs of the residuals in cumulative number of deaths in Hubei.

TS Model-based method for estimation in the united states

Based on the given data of America, we use the expert modeler to process the data and we find that all of the cumulative number of diagnoses, deaths and cures conform the ARIMA model. However, the parameters setting of each group of them are not identical.

After processing, it is found that the cumulative diagnoses in the United States applies the ARIMA (2, 2, 6) model. The corresponding equation is the same with equation.

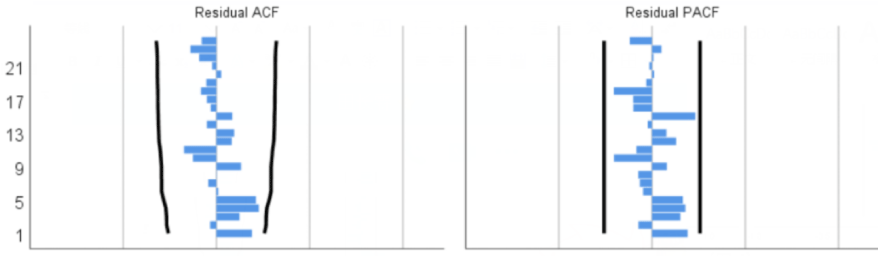
Next, we performed a residual test on the model based on white noise. As can be seen from Figure 5, the ACF and PACF graphs of the residuals, the autocorrelation coefficients and partial correlation coefficients of all lag orders are not significantly different from 0. From Figure 6, it can also be seen that the P value obtained from the Q test of the residual is 0.304, that is, we cannot reject the null hypothesis, and think that the residual is a white noise sequence.

Figure 5: The ACF and PACF graphs of the residuals in cumulative number of diagnoses in U.S. case.

Figure 6: The Q test on the residual of the case of cumulative number of diagnoses in U.S. case.

Therefore, the ARIMA (2,2,6) model can well describe the cumulative number of diagnoses.

The cumulative number of cures conforms ARIMA (0, 2, 0) model, which is equal to 2nd order difference equation. The related equation set is similar to the equation .

As usual, we should use white noise to perform a residual test. As the Figure 7 shows below, the ACF and PACF graphs of the residuals can be seen that the autocorrelation coefficients and partial correlation coefficients of all lag orders are not significantly different from 0.

Figure 7: The ACF and PACF graphs of the residuals in cumulative number of cures in U.S. case.

At last, we use expert modeler to process the data of cumulative deaths in U.S., then it is found that it conforms the ARIMA (0, 2, 1) model. The related equation set still conforms with the equation .

Then we perform a white noise residual test. As can be seen from Figure 8, the ACF and PACF graphs of the residuals, the autocorrelation coefficients and partial correlation coefficients of all lag orders are not significantly different from 0.

Figure 8: The ACF and PACF graphs of the residuals in cumulative number of deaths in U.S. case.

Results

The TS Model-based method results in hubei province

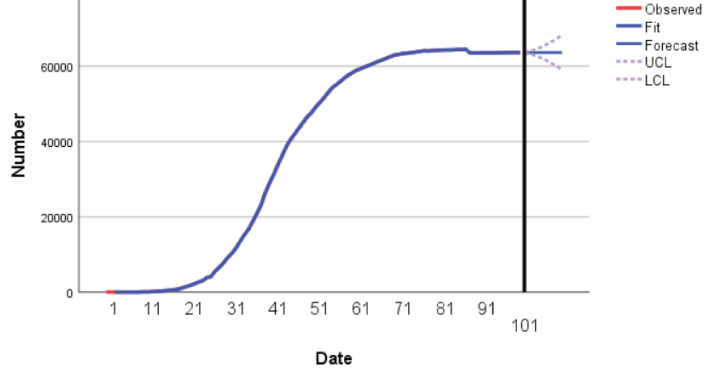
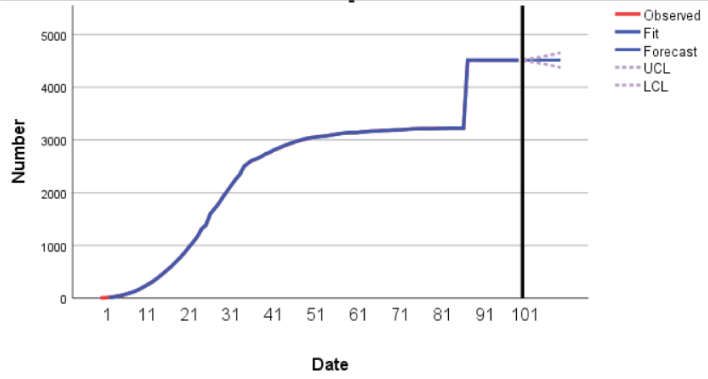
We set the width of the confidence interval to 95%, then use the Holt model and ARIMA model to fit and predict the cumulative number of people diagnosed, cumulatively cured and cumulatively died in Hubei Province respectively. The obtained results shown in the following figures.

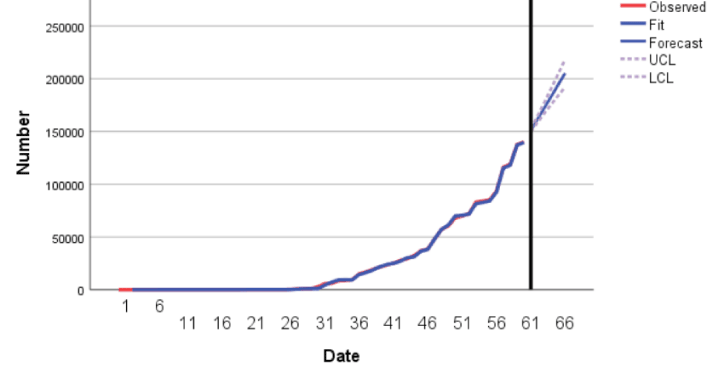
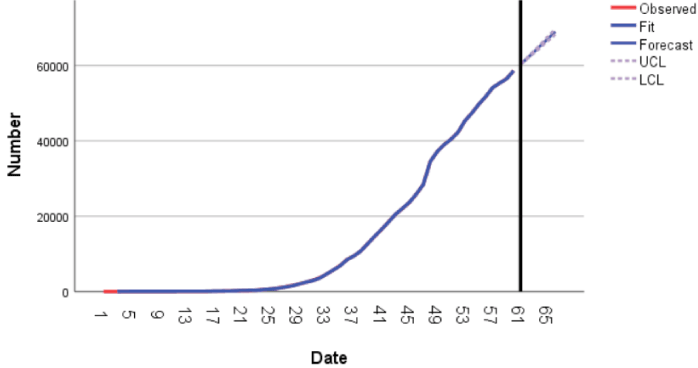
As can be seen in the Figure 9-11, the time series plots of the real and fitted data almost overlap, and the Holt and ARIMA models fit the original data well.

At the same time, after 28 April, the epidemic situation in Hubei Province has been controlled, and the cumulative number of diagnoses will basically not increase dramatically. The Holt model and ARIMA model can also well predict the cumulative diagnoses, cumulative cures and cumulative deaths. The Table 6 listed below contains the predicted values of cumulative number of diagnoses, cures and deaths in Day 101 to 105 by using the equationand the Figure 9-11.

Figure 9: The cumulative number of diagnoses in Hubei Province.

Figure 10: The cumulative number of cures in Hubei Province.

Figure 11: The cumulative number of deaths in Hubei Province.

The TS Model-based method results in the united states

Our analysis of the U.S. epidemic situation also set the width of the confidence interval to 95%. The results obtained by fitting and predicting the number of cumulative diagnoses, cumulative cures and cumulative deaths using the ARIMA model are shown in the following figures.

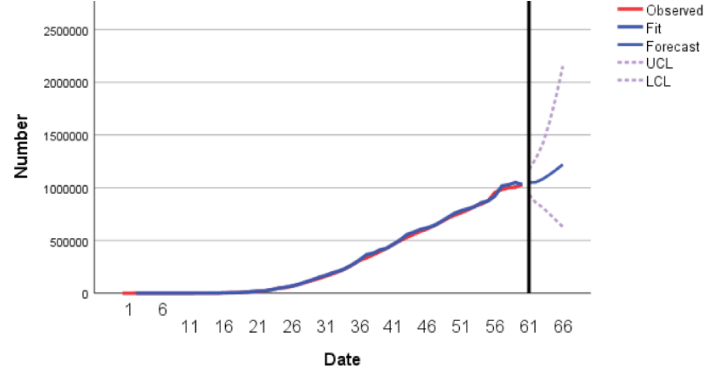
It can be seen from Figures 12-14, the time series plots of the real and fitted data almost overlap, and the Holt and ARIMA models fit the original data well.

Figure 12: The cumulative number of diagnoses in U.S.

Figure 13: The cumulative number of cures in U.S.

Figure 14: The cumulative number of deaths in U.S.

At the same time, after 28 April, the cumulative number of diagnoses, cumulative deaths and cumulative cures will continue to increase substantially in the short term, which is related to the policies adopted by the US government to combat the epidemic. This shows that the ARIMA model can also predict the cumulative diagnoses, cumulative deaths and cumulative cures.

The specific predicted values of cumulative number of diagnoses, cures and deaths in Day 61 to 65 are listed in the Table 7 below.

Discussion

At the time of the virus outbreak, everyone is living in panic, fearing for their lives and the lives of their families and the safety of the country.

We use SPSS [12], to accurately get the models we need, such as Holt model and ARIMA model, and then use these models to fit the sequences, and estimate the model parameters based on the sequence values. Finally, we perform residual tests on the models with white noise to check whether the model is applicable.

Time series analysis of COVID-19 gives the course, direction and trend of the epidemic and predicts the likely development of future epidemics to what state. This will give us some guidance in our lives, such as in the response to the epidemic what measures should be taken to intervene in the development of the epidemic, to save more lives.

We can see from the results that not only the epidemic situation of China and the United States selected period is different, but also in epidemic development after 60 days or so. It can be seen that outbreak in the United States will continue to present an exponential growth, but the epidemic situation of Hubei province is basically controlled, probably around 100 days in Hubei province in May outbreak was completely under control. The outcome of the epidemic is different, which is largely related to the measures taken by the country to combat the epidemic, as can be seen from the attitude of China and the United States towards the epidemic [13]. That’s why it’s important to have the right understanding in the face of an epidemic, and not to be blindly arrogant and underestimate the seriousness and potential dangers of an epidemic.

Time series can not only be used in the analysis of infectious diseases, but also in many social disciplines such as measurement [14] and economy [15]. The data order and size in time series contain the information of the objective world and its changes, and represent the dynamic process. Therefore, the main purpose of time series analysis is to understand the considered dynamic system, predict future events, and control future events through intervention [16,17].

Limitations

When establishing the model, we regard the data with large fluctuations as outliers. In fact, there are many more complex models that can catch these outliers. At the same time, when we make predictions, the ARIMA model is only suitable for short-term prediction. Over a certain period of time, the predicted value will not change any more, due to the theory of the model. So when solving this problem, we can assume the predicted values as the observed values, thus the long-term prediction would be possible, but the difference between the truly observed data might be larger and larger.

Since the epidemic is only predicted in the short term, it can be seen from the analysis chart of epidemic situation in the United States that the cumulative number of people who are cured, died and diagnosed, cases are all moving in an increasing direction. However, in practice, the number of people in these categories should reach a stable value in the end.

This work was supported by the Philosophical and Social Sciences Research Project of Hubei Education Department (19Y049), and the Staring Research Foundation for the Ph.D. of Hubei University of Technology (BSQD2019054), Hubei Province, China.

1. Link: https://bit.ly/3dWhpU5
2. Link: https://bit.ly/2NPHda8
3. Link: https://bit.ly/3dPv13K
4. Link: https://bit.ly/2ZAiXyi
5. Xuan Z (2019) Epidemiological characteristics and time series analysis of hand, foot and mouth disease in Wuzhou City from 2014 to 2018. Nanning:Guangxi Medical Universit.
6. Xiaonan H, Xiaohui S, Xin Z (2019) Prediction of hand-foot-mouth disease incidence in Luoyang based on ARIMA model[J]. Modern Preventive Medicine.
7. Xiaodi Y (2019) Epidemiological characteristics and time series analysis of hemorrhagic fever in nephrotic syndrome in Jilin province[D]. Changchun:Jilin University. (in Chinese)
8. Wenli S, Liting Z, Shichao L, et al.  (2018) Dynamic prediction of oil well production based on Holt exponential smoothing model[J]. Automation and Instrumentation 033: 68-70.
9. Link: https://bit.ly/38jbkjD
10. Link: https://bit.ly/3eUqtdz
11. Link: https://bit.ly/2BmA66x
12. Link: https://bit.ly/31BmMFV
13. Link: https://bit.ly/3ghfET3
14. Tonghe S (2013) Application of time series analysis in the field of measurement. Mapping and Spatial Geographic Information. 036: 12-13.
15. Lan G (1994) The application of time series analysis to the economy. Beijing: China Statistics Press.
16. Yongdao Z (2015) Time series analysis and applications. Beijing: Higher Education Press.
17. Shuyuan H (2007) Applied time series analysis [M]. Beijing: Peking University Press. (in Chinese).