Dynamic model of infectious diseases on the coronavirus disease 2019

Under the general trend of globalization, historically and newly discovered infectious diseases are seriously threatening people’s health and lives, including: Avian influenza H7N9, AIDS HIV, Influenza A H1N1, etc., a new type of corona that is currently spreading in many countries around the world Viral pneumonia (C0VID-19), there is currently no good therapeutic drug, which seriously affects human survival and development. The rapid spread of the new coronavirus in Hong Kong, while starting the epidemic prevention work, uses mathematical modeling methods to construct the propagation model, and then calculates the inflection point for better prevention and control of the spread of epidemic work. The spread of Hong Kong was analyzed, and the quantitative relationship between the growth rate of the number of new coronavirus infections and time was explored.

In order to find out and predict the impact on the spread of infectious diseases, we established a class of kinetic models, gave formulas for calculating numbers, analyzed inflection points and predicted the development trend of new coronaviruses, and used C0VID-19 as an example for numerical simulation .

Background: In December 2019, China’s first unexplained pneumonia patient was admitted to Wuhan Jinyintan Hospital, Hubei, China. Since then, COVID-19 has expanded rapidly in Wuhan, Hubei, China. Within a few months, COVID-19 soon It spread to 34 provincial administrative regions and neighboring countries across China, and Hubei Province immediately became the hardest hit by the new coronavirus.

New coronavirus pneumonia (COVID-19) As of April 17, 2020, the cumulative number of confirmed cases in China was 83,824, the cumulative number of deaths was 3352, the cumulative number of foreign diagnoses was 2,090000, and the cumulative deaths were 141,601. The outbreak and spread of COVID-19 have seriously affected people’s Good health has caused huge economic losses in our country. It is of far-reaching significance to explore effective prevention and control of infectious diseases and minimize the harm caused by infectious diseases.

In an emergency situation, we strive to establish an accurate infectious disease dynamic model to predict the development and spread of COVID-19, and make some effective short-term predictions on this basis. The construction of this model is relevant to all aspects of mainland China. It is helpful for the department to carry out the prevention and monitoring of the new coronavirus. It also strives for more time for the clinical trials of Chinese researchers and the research of vaccines against the virus to eliminate the new coronavirus as soon as possible.

Methods: Collect and compare and integrate the spread of COVID-19 in Hong Kong, record the spread of the virus in the population and the protest measures of relevant government departments, and establish a dynamic model of infectious diseases based on the original data changes.

Interpretation: In the early stage of the epidemic, due to inadequate anti-epidemic measures, the epidemic in Hong Kong quickly spread. However, with the gradual understanding of COVID-19, the epidemic began to be gradually controlled, and then the growth was blocked.

Introduction

After the outbreak of COVID-19 in China, COVID-19 also broke out in Hong Kong [1,2]. The spread of new coronary pneumonia and various measures have had an inestimable impact on people’s daily lives and the normal functioning of society.

In fact, there are some urgent problems to be solved about the spread of COVID-19. Can existing interventions effectively control COVID-19? Can you elaborate on the changes and development characteristics of each epidemic situation? Can we combine the conclusions found in the comparison of Hong Kong’s actual population, medical level, traffic conditions, geographical location, customs and culture, and anti-epidemic measures? What mathematical model can we build to solve the problem?

COVID-19 is a new coronavirus discovered in December 2019. The epidemic data is not sufficient, and clinical methods such as clinical trials are still in the exploration stage. So far, the epidemic situation data is difficult to apply directly to the existing mathematical model. The problems to be solved are: how effective the existing emergency response is, how to invest medical resources more scientifically in the future, etc. On this basis, this article aims to study the shortcomings of this part [3-10].

Methods

Data

The epidemiological data we obtained comes from the Microsoft Bing website, and the data is official and reliable.

The model

According to the collected epidemic data, we try to find out the transmission law of COVID-19 and put forward effective prevention and control methods.

There are generally three methods for systematically studying the spread of infectious diseases. One is to establish a dynamic model of infectious diseases. The second is statistical modeling using statistical methods such as random processes and time series analysis. The third is to use data mining technology to obtain information in the data and discover the epidemic law of infectious diseases. Using the collected data on infection of new coronary pneumonia in Hong Kong, China [11,12], this article mainly uses the first and second methods.

In this paper, the SIR prediction model for the spread of COVID-19 is established, and the prediction effect of the mathematical model for the spread of COVID-19 epidemic is compared Figure 1.

Figure 1: SIR model.

Dynamic equation

ds(t)=-βi(t)s(t)

di(t)/dt=βi(t)-γi(t)

dr(t)/dt=γi(t)

Based Logistic estimated square law

The traditional Logistic model can not describe the different developments of the epidemic well. After analyzing the actual situation and the existing data, we have established a more effective SIR infectious disease transmission model. According to the actual situation of the epidemic, our relevant data indicators in Hong Kong, China (cumulatively confirmed cases, cumulative deaths, newly diagnosed cases per day, cumulative number of cured cases, existing confirmed cases) are analyzed to adapt to the current situation of the new coronary pneumonia epidemic in various parts of the world propagation Table 1.

Because there are suspected cases, it is reasonable for the susceptible population that the infected person can reach without taking the total number of Hong Kong as unknown [13-18].

In addition, the number of daily stays in the hospital is defined as the number of infected persons, and the cumulative number of discharges and deaths is defined as the number of people who are moved out.

as follows:

It= number of daily hospitalization = cumulative confirmed number-cumulative discharge number-cumulative discharge and number of death Rt=Cumulative discharges and deaths

From the data, we can know that the cumulative death toll in Hong Kong, China over time is a nonlinear process, considering The dynamic model of infectious diseases, here we use SIR prediction model to fit.

Here we use SIR prediction model to fit the dynamic model of infectious diseases.

Simulation

Because COVID-19 has been developing in Hong Kong, China for a long time, and the cumulative number of confirmed cases is more convincing, so here we use the cumulative number of confirmed cases in Hong Kong, China to turn this nonlinear model into a linear model, And use matlab for fitting linear regression analysis [19,20].

Objective function code of genetic algorithm Figure 2:

Figure 2: Brief process of using settings in the genetic code toolbox.

Function ra=optSIR (X)

% beta=0.00002;

% gamma=1/20;

Beta=X (1) / 1e6;

Gamma=X (2) / 1e2;

S0 ≤ X (3) * 1e4;

X0 = [S0, 25, 2];

Ts=0:1:300;

[t, x] = ode45 (@ (t, x) SIRModel (t, x, beta, gamma), ts, x0);

I = [7621 5768 4696 3747 2857 2364 2042 1721 1458 578 526 502 440 227 169 41 28 27 25];

R = [730 616 446 362 358 275 219 184 132 120 92 70 55 31 21 17 14 02];

T = [35 34 33 32 31 30 29 28 27 26 25 24 23 20 19 17 16 150];

IntensifiedPoint=15;

IP=intensifiedPoint;

Omega= [iP 1 1 1];

Eps_I=0;eps_R=0;

For i=1:length (T)

Eps_I=eps_I+omega (i) * (x (T (i) + 1, 2)-I (i)) ^ 2 ≤ I (i) ^ 2;

Eps_R=eps_R+omega (i) * (x (T (i) + 1, 3)-R (i)) ^ 2 ≤ R (i) ^ 2;

% eps_I=eps_I+omega (i) * (x (T (i) + 1, 2)-I (i)) ^ 2;

% eps_R=eps_R+omega (i) * (x (T (i) + 1, 3)-R (i)) ^ 2;

End

OmegaI=1e0;

Ra= (omegaI*sqrt (eps_I) + sqrt (eps_R)) / length (T);

IsPlot=0;

If IsPlot==1

Plot (t, x (:, 1),’k, t, x (:, 2),’r, t, x (:, 3),’b ‘); hold on

Xlabel (‘time / day’);

Ylabel (‘number of people’);

Legend (‘S, I, R’);

Plot (T, I, o ‘); hold on)

Plot (T, R, Bo ‘); hold off)

End

End

Function y=SIRModel (t, x, beta, gamma)

Y = [- beta*x (1) * x (2), beta*x (1) * x (2)-gamma*x (2), gamma*x (2)]’;

End

Drawing code

Clear

IsPlot=1;

Ra= [24.77762843006681 0.01910894953088675 0.7805747296079624];

Beta=ra (1) * 1e ≤ 6;

Gamma=ra (2) * 1e ≤ 2;

S0=ra (3) * 1e4;

X0 = [S0, 25, 2];

Ts=0:1:300;

[t, x] = ode45 (@ (t, x) SIRModel (t, x, beta, gamma), ts, x0);

I = [7621 5768 4696 3747 2857 2364 2042 1721 1458 578 526 502 440 227 169 41 28 27 25];

R = [730 616 446 362 358 275 219 184 132 120 92 70 55 31 21 17 14 02];

I ≤ S _ 0 / R / S _ 0;

T = [35 34 33 32 31 30 29 28 27 26 25 24 23 20 19 17 16 150];

% The data is from Wuhan city only. The data source cannot be revealed because it is related to sensitive word (Wuhan Wei Jian Wei and Hubei WJW).

If IsPlot==1

Figure

X / x / S _ 0;

Plot (t, x (:, 1),’k, t, x (:, 2),’r, t, x (:, 3),’b ‘); hold on

Xlabel (‘time / day’);

Ylabel (‘proportion’);

Plot (T, I, o ‘); hold on)

Plot (T, R, Bo ‘); hold off)

Legend (‘Susceptible crowd’, ‘Predicted value of infected people’, ‘Predicted value of rehabilitation population’, ‘The actual value of infected people’, ‘Actual value of rehabilitation population’);

Axis ([0300,01])

End

Function y=SIRModel (t, x, beta, gamma)

Y = [- beta*x (1) * x (2), beta*x (1) * x (2)-gamma*x (2), gamma*x (2)]’;

End

Results

SIR model estimates

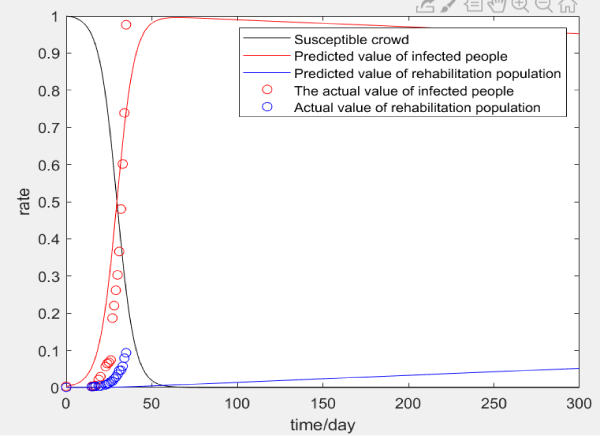
Based on the cumulative number of confirmed cases in Hong Kong, China, we used Matlab to establish the SIR prediction model and performed linear regression analysis. Using the above processing, we can get the predicted cumulative number of confirmed cases in Hong Kong, China as shown in Figure 3.

As shown in Figure 3, we can conclude that when the amount of data is large, it can be seen that the effect of fitting is not particularly good.

Figure 3: Simulation of infected people and recovered people.

Discussion

In the early stages of the transmission of COVID-19, it is difficult to establish a SIR model and parameter estimation and obtain a fairly accurate simulation result, but the initial estimated parameters such as the growth rate of the confirmed cases and the possible cumulative maximum confirmed cases can be obtained through existing data. It is helpful to solve important parameters such as infection rate and recovery rate, which will help us to grasp the transmission trend of COVID-19 more accurately. On the other hand, the statistical model of the spread of the new coronavirus in the population analyzed by the SIR model is something that can be done immediately after obtaining the latest data every day. Although this method usually requires enough data to support it, in the early stages of epidemic transmission, this method can still be used to predict the indicators of epidemic transmission, thus providing control departments and policy implementation in the population at various stages provides a short-term Emergency prevention plan [21-25].

Limitations

1. Promotion of the model: A logistic model based on 2019-nCoV can be established. The logistic model is superior to the SIR model in accuracy, but because the SIR parameters need to consider more parameters, the calculation error is greater than the logistic model.

2. A dynamic growth rate model based on 2019-nCoV can be established. The dynamic growth rate model has a good fitting effect, but has a certain error.

3. You can also optimize on the value of S0, you can optimize on the calculation method of I, R, and update the data in real time.

4. When the amount of data is large, due to the large number of parameters to be considered, the error is large.

Conflict of interest

We have no conflict of interests to disclose and the manuscript has been read and approved by all named authors.

This work was supported by the Philosophical and Social Sciences Research Project of Hubei Education Department (19Y049), and the Staring Research Foundation for the Ph.D. of Hubei University of Technology (BSQD2019054), Hubei Province, China.

1. National Health Commission of the People’s Republic of China. Link: https://bit.ly/3hdSQ87
2. National Health Commission of the People’s Republic of China. Link: https://bit.ly/2AVd6L4
3. Dye C, Gay N (2020) Modeling the SARS epidemic. Science 300: 1884-1885. Link: https://bit.ly/2YilTio
4. Riley S, Fraser C, Donnelly CA (2020) Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science 300: 1961-1966. Link: https://bit.ly/3dREhFb
5. de Oliveira E M, Oliveira FLC (2020) Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy14: 776-788. Link: https://bit.ly/2MI2QIM
6. Chen P, Yuan H, Shu X (2020) Forecasting crime using the arima mode. 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery. IEEE 18: 627-630. Link: https://bit.ly/2UtZxJz
7. Li X (2020) Comparison and analysis between holt exponential smoothing and brown exponential smoothing used for freight turnover forecasts. IEEE 15: 453-456. Link: https://bit.ly/2UsynCX
8. Hansun S (2016) A New Approach of Brown’s Double Exponential Smoothing Method in Time Series Analysis. Balkan Journal of Electrical and Computer Engineering 4: 75-78. Link: https://bit.ly/3fcZs54
9. Chadsuthi S, Modchang C, Lenbury Y (2020) Modeling seasonal leptospirosis transmission and its association with rainfall and temperature in Thailand using time–series and ARIMAX analyses. Asian Pacific journal of tropical medicine 5: 75-78.
10. Ming W, Huang J, Zhang CJP (2020) Breaking down of healthcare system: Mathematical modelling for controlling the novel coronavirus (COVID-19) outbreak in Wuhan, China. bioRxiv 12: 627-630. Link: https://bit.ly/3dSX17s
11. Chowell G, Castillo-Chavez C, Fenimore PW (2020) Model parameters and outbreak control for SARS. Emerg Infect Dis 9: 75-8.
12. Luo H, Ye F, Sun T, Yue L, Peng S, et al. (2020) In vitro biochemical and thermodynamic characterization of nucleocapsid protein of SARS[J]. Biophysical chemistry 6: 76-78.
13. Colizza V, Barrat A, Barthélemy M  (2020) Predictability and epidemic pathways in global outbreaks of infectious diseases: the SARS case study. BMC Med  8: 95-101.
14. Tsui W H K, Balli H O, Gower H (2020) Forecasting airport passenger traffic: the case of Hong Kong International Airport. 6: 75-78.
15. National Health Commission of the People’s Republic of China. Link: https://bit.ly/37sNulb
16. World Health Organization (WHO). Coronavirus. Link: https://bit.ly/2Yp5xUW
17. National Health Commission of the People’s Republic of China. Link: https://bit.ly/30t8sP2
18. Health Commission of Hubei Province. Link: https://bit.ly/3cPHeF0
19. Health Commission of Hubei Province.  Link: https://bit.ly/3fm6J2z
20. National Health Commission of the People’s Republic of China. Link: https://bit.ly/2MLtaBQ
21. Health Commission of Hubei Province.  Link: https://bit.ly/2XLKInI
22. Wu P, Hao X, Lau EHY, Wong YJ, Leung KSM, et al. (2020) Real-time tentative assessment of the epidemiological characteristics of novel coronavirus infections in Wuhan, China. Eurosurveillance 25: 2000044. Link: https://bit.ly/2XNbo7p
23. National Health Commission of the People’s Republic of China. Link: https://bit.ly/3hcgcer
24. National Health Commission of the People’s Republic of China. Link: https://bit.ly/37i98bu
25. Health Commission of Hubei Province.  Link: https://bit.ly/2MOy9S4