Introduction
We present a classical Poisson manifold approach, closely related to construction of integrable Hamiltonian systems, generated by nonassociative and noncommutative algebras. In particular, we devise its natural and simple generalization, useful for describing a wide class of Lax type integrable nonlinear Hamiltonian systems on associative noncommutative algebras, initiated first in [1-4], in case of the associative noncommutative operator algebras and continued later in [5-11], in case of general associative noncommutative algebras.
Poisson structures on non commutative functional manifolds
It is interesting to look at construction of the Hamiltonian operators and revisit it from the classical point of view, considering them as those defined on the naturally associated [4,12-17], cotangent space
to some linear functional noncommutative manifold M
where
is, in general, a (non)associative noncommutative algebra over a field
, and
is its naturally adjoint space. Then, a Hamiltonian operator on M is defined [12,15], as a smooth mapping
such that for any fixed
the bracket
where
are arbitrary smooth mappings from the functional space
satisfies the Jacobi identity. The bracket (2.1) is determined on M by means of the natural convolution
on the product
and respectively, the gradient
of a function
is calculated as
for any
It is well known [18,19], that a linear operator
determined at any point
is Hamiltonian iff the suitably defined [18], Schouten–Nijenhuis bracket
identically on M Namely, this condition (2.3) was used in the investigations [18,20], to formulate criteria for the operator
to be Hamiltonian on the functional manifold M. Yet these criteria appear to be very complicated and involve a large amount of cumbersome calculations even in the case of fairly simple differential expressions. So, we have reanalyzed this problem from a slightly different point of view. First, recall that the Jacobi identity for the bracket (2.1) is completely equivalent to the fact that the bracket operator defined as
for a fixed
and arbitrary
acts as a derivation on the space
where
are taken arbitrary. This can be easily reformulated as follows: take any element
such that the Fréchet derivative
at any
with respect to the convolution
on
and construct a vector field
as
Then the derivation condition (2.4) can be equivalently rewritten [4,12,15-17], as the strong Lie derivative
along the vector field
at any
for all “self-adjoint” elements
Equivalently, a given linear skew-symmetric operator
is Hamiltonian iff the Lie derivative (2.6) vanishes for all “self-adjoint” elements
Moreover, as was observed in [21], it suffices to check the condition (2.6) only on the subspace of elements
satisfying the condition
for any
As an example, one can check that a skew-symmetric matrix-differential operator on M of the form
where, an -dimensional square matrix
satisfies the condition (2.6) iff the linearly independent elements from
generate the finite dimensional nonassociative Balinsky-Novikov algebra [22] and satisfy the conditions
for all
Similarly, one can verify that the skew-symmetric inverse-differential operator
where, as above
the sign
means the usual matrix transposition, is Hamiltonian iff the basic nonassociative algebra
coincides with the right Leibniz algebra [23] and the condition
holds for any
. The skew-symmetric inverse-differential operator (2.8) can be naturally generalized to the expression
which can be rewritten as
where, by definition,
and
for all
The condition (2.6) for the operator (2.10) to be Hamiltonian reduces to the constraints on the related nonassociative algebra
exactly coinciding with those, analyzed in some detail in [24] .
As it was already mentioned [18,24], based on the matrix representations of the right Leibniz algebra and the new nonassociative Riemann algebra, one can construct many nontrivial Hamiltonian operators
on the adjacent weak Lie algebra
related with diverse types of nonassociative noncommutative algebras
These Hamiltonian operators prove to be very useful [25,26,27], for describing a wide class of multicomponent hierarchies of integrable Riemann type hydrodynamic systems and their various physically reasonable reductions.
Poisson structures on manifolds generated by associative non commutative algebras
Proceed now to a slightly generalized construction of Hamiltonian operators on a phase space, generated by associative noncommutative algebra A-valued matrices, which was first studied in [1-4], in case of the noncommutative operator algebras and continued later in [5-11], in case of general associative noncommutative algebras. This natural and simple generalization appeared to be very useful [28,29,30,31,8-10], for describing a wide class of new Lax type integrable nonlinear Hamiltonian systems on associative noncommutative algebras, interesting for diverse applications in modern quantum physics.
We start here with a free associative noncommutative algebra
generated by a finite set of elements
and define its “abelianization”
and the projection
where the space
Consider now a naturally related with A n-dimensional matrix Lie algebra
over the field
with entries in A subject to the usual matrix commutator
for all
Being first interested in the Lie-algebraic studying [14,15,32,33], of co-adjont orbits on the adjoint space
let us construct a bi-linear form
on the Lie algebra
by means of the trace-type expression
for any
The following important lemma holds.
Lemma 3.1 The bilinear form (3.1) on
is symmetric, nondegenerate and ad-invariant.
Proof. Symmetricity: We have:
for any
Nondegeneracy: Assume that
for a fixed
and all
state that
let us put then
and obtain
Taking into account that the associative algebra is generated by the finite set of elements
it is easy to deduce from
expansions of elements
from A that the sum
iff
for all
Really, the sum of (3.5) under the
-mapping can be now rewritten, respectively, as
with some D-coefficients from
for all
depending quadratically on coefficients of expansions, staying at uniform and symmetric basis elements of the algebra A As the
-mapping sends all of them, by definition, to zero, the resulting system (3.5) reduces to the set of algebraic equations
reducing successively for all
to the condintions
being equivalent to the equalities
for all
As a simple consequence from Lemma 3.1 one derives the next proposition.
Proposition 3.2 The construted Lie algebra
is ad-invariant and
-metrized.
Proof. Really, from the symmetry property (3.2) one easily obtains that
modulo
-mapping for any elements a,b and
As the bilinear form (3.1 is non-degenerate, one has
that jointly with the ad-invariance property (3.9) means that the Lie algebra
is metrized.
Being interested in constructing integrable noncommutative dynamical systems on the algebra A we need to introduce into our analysis a “spectral” parameter
responsible for the existence of infinite hierarchies of the corresponding dynamical systems invariants, guaranteeing their integrability. This wil be done in next Section, devoted to the Lie-algebraic analysis on loop-Lie-algebras, related with the Lie algebra
introduced above.
Consider now the Lie algebra
constructed above, and the related loop Lie algebra
of the corresponding
-valued Laurent series with respect to the parameter
and define on it the corresponding to (3.1) modulo
-mapping bilinear form
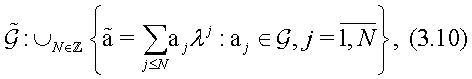
and define on it the corresponding to (3.1) modulo
-mapping bilinear form 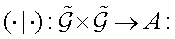
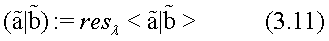
for any elements 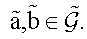 It is easy to observe that the bilinear form (3.11) is also symmetric and non-degenerate. Thus, the following proposition holds.
It is easy to observe that the bilinear form (3.11) is also symmetric and non-degenerate. Thus, the following proposition holds.
Proposition 3.3 The loop Lie algebra
is ad-invariant and
-metrized.
As the loop Lie algebra
allows natural direct sum splitting
into two Lie subalgebras
and
where
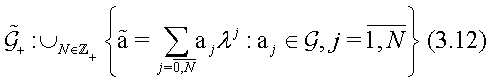
and
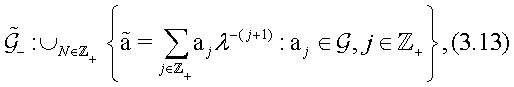
their adjoint spaces with respect to the bilinear form (3.11) split the adjoint loop space
and satisfy the equivalences
and
Let now a linear endomorphism
equal
where, by definitions,
are the projections on the corresponding subspaces It is a well known property [14,15,32,33] that the deformed Lie product
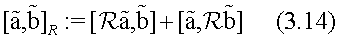
for any 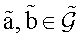 satisfies the Jacobi condition and generates on the loop Lie algebra
a new Lie algebra structure.
satisfies the Jacobi condition and generates on the loop Lie algebra
a new Lie algebra structure.
Within the classical Adler-Kostant-Symes Lie-algebraic approach, or its
-matrix structure generalization [14,15,32,33], the adjoint loop space
is then endowed with the modified Lie-Poisson structure

for any basic functionals 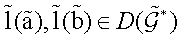 subject to which the whole set
subject to which the whole set
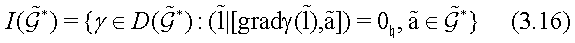
of smooth Casimir functionals on
is commutative with respect to the deformed Lie-Poisson structure (3.15) on
that is
for all
and, by definition, 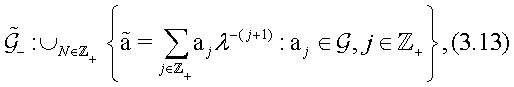 The latter makes it possible to construct integrable Hamiltonian flows on the associative algebra A as Poissonian flows on the co-adjoint orbits on the adjoint space
generated by suitable loop Lie algebra
Casimir gradient elements. Namely, if an element
The latter makes it possible to construct integrable Hamiltonian flows on the associative algebra A as Poissonian flows on the co-adjoint orbits on the adjoint space
generated by suitable loop Lie algebra
Casimir gradient elements. Namely, if an element 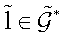 is fixed, the corresponding Hamiltonian flow on
subject to the deformed Poisson bracket (3.15) and a Casimir funcrtional
possesses the well known Lax type [33-40], representation
is fixed, the corresponding Hamiltonian flow on
subject to the deformed Poisson bracket (3.15) and a Casimir funcrtional
possesses the well known Lax type [33-40], representation
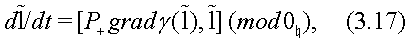
where
is a related evolution parameter. The example of this construction and its Lie algebraic properties are discussed in the next Subsection.
Kontsevich type integrable systems on unital finitely generated free associative noncommutative algebras
Let a free unital finitely generated associative non-commutative algebra
be the corresponding group algebra of a group
generated by two elements
The algebra A is infinite dimensional with the countable basis
the related two-dimensional matrix loop Lie algebra
is metrized subject to the bi-li near product (3.11) and generated by affine elements
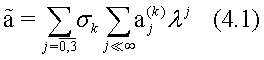
with four basis Pauli matrix elements
and algebra components
The corresponding Casimir functionals
generate a Hamiltonian flow on points 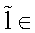 with respect to the Poisson bracket (3.15) in the Lax type form (3.17). To analyze this flow in detail, let us put, by definition, that the seed orbit point
with respect to the Poisson bracket (3.15) in the Lax type form (3.17). To analyze this flow in detail, let us put, by definition, that the seed orbit point 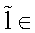 is given by the following
-squared expression
is given by the following
-squared expression
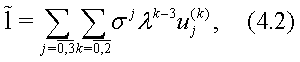
where
is the dual basis of the matrix space
and elements
are coordinates of some A-algebra valued phase space
in a general position. In particular, we will choose the following dual bases:
in
and
in
Moreover, we also will assume that A-algebra valued coefficients of the phase space
in (4.2) are representable subject to the basis of A as
following the result obtained in [31].
As a first important task, we will calculate the corresponding Poisson structure on the related A-algebra valued phase space 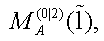 generated by coefficients, presented in the expression (4.4). To do this, we need to take into account that the phase space
generated by coefficients, presented in the expression (4.4). To do this, we need to take into account that the phase space 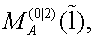 being endowed with the
-modified Poisson structure (3.15), is strongly reduced via the Dirac scheme [4,32], subject to the set
being endowed with the
-modified Poisson structure (3.15), is strongly reduced via the Dirac scheme [4,32], subject to the set
of algebraic constraints, imposed on the phase space
The latter means that the true Poisson structure on the reduced phase space 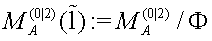 coincides with the corresponding Dirac type reduction of the
-modified Poisson structure, defined on the full phase space
As a result of simple enough yet cumbersome calculations we arrive at the following Poisson brackets
coincides with the corresponding Dirac type reduction of the
-modified Poisson structure, defined on the full phase space
As a result of simple enough yet cumbersome calculations we arrive at the following Poisson brackets
on the reduced phase space 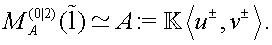
Having taken as a Hamiltonian operator 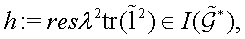 one easily obtains the following [5], nonlinear integrable Kontsevich dynamical system
one easily obtains the following [5], nonlinear integrable Kontsevich dynamical system
on the reduced phase space
Moreover, owing to the Lax type representation (3.15), the Kontsevich dynamical system (4.7) proves to be equivalent to the following matrix commutator equation
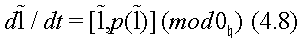
for any
in the Lie algebra
where the A-valued matrix 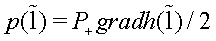
Taking as Hamiltonian functions the algebraic expressions 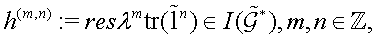 one can obtain a complete set of
-commuting to each other conservation laws of the Kontsevich dynamical system (4.7), thus proving its generalized integrability. Moreover, choosing both another group algebra and orbit elements
one can obtain a complete set of
-commuting to each other conservation laws of the Kontsevich dynamical system (4.7), thus proving its generalized integrability. Moreover, choosing both another group algebra and orbit elements 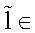 one can construct the same way many other integrable Hamiltonian systems on the associative noncommutative phase space A, that is planned to be a topic of a next investigation.
one can construct the same way many other integrable Hamiltonian systems on the associative noncommutative phase space A, that is planned to be a topic of a next investigation.
Conclusion
In this work we succeeded in revisting the classical Poisson manifolds approach to Hamiltonian operators on functional noncommutative manifolds, as well as presented it simple and natural realization, generated by associative noncommutative group algebra. The latter appeared to be very useful for describing a wide class of new Lax type integrable nonlinear Hamiltonian systems on associative noncommutative algebras, interesting for diverse applications in modern quantum physics.
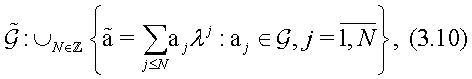
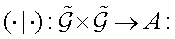
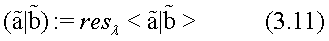
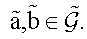 It is easy to observe that the bilinear form (3.11) is also symmetric and non-degenerate. Thus, the following proposition holds.
It is easy to observe that the bilinear form (3.11) is also symmetric and non-degenerate. Thus, the following proposition holds.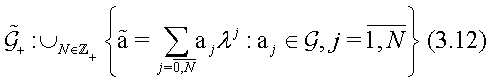
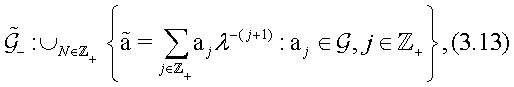
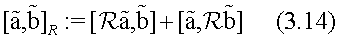
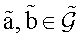 satisfies the Jacobi condition and generates on the loop Lie algebra
a new Lie algebra structure.
satisfies the Jacobi condition and generates on the loop Lie algebra
a new Lie algebra structure. 
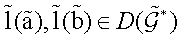 subject to which the whole set
subject to which the whole set 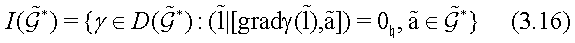
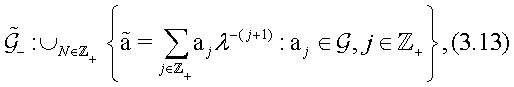 The latter makes it possible to construct integrable Hamiltonian flows on the associative algebra A as Poissonian flows on the co-adjoint orbits on the adjoint space
generated by suitable loop Lie algebra
Casimir gradient elements. Namely, if an element
The latter makes it possible to construct integrable Hamiltonian flows on the associative algebra A as Poissonian flows on the co-adjoint orbits on the adjoint space
generated by suitable loop Lie algebra
Casimir gradient elements. Namely, if an element 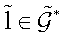 is fixed, the corresponding Hamiltonian flow on
subject to the deformed Poisson bracket (3.15) and a Casimir funcrtional
possesses the well known Lax type [33-40], representation
is fixed, the corresponding Hamiltonian flow on
subject to the deformed Poisson bracket (3.15) and a Casimir funcrtional
possesses the well known Lax type [33-40], representation 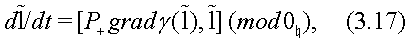
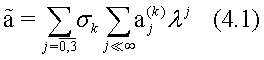
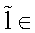 with respect to the Poisson bracket (3.15) in the Lax type form (3.17). To analyze this flow in detail, let us put, by definition, that the seed orbit point
with respect to the Poisson bracket (3.15) in the Lax type form (3.17). To analyze this flow in detail, let us put, by definition, that the seed orbit point 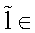 is given by the following
-squared expression
is given by the following
-squared expression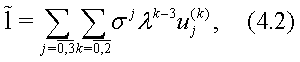
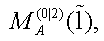 generated by coefficients, presented in the expression (4.4). To do this, we need to take into account that the phase space
generated by coefficients, presented in the expression (4.4). To do this, we need to take into account that the phase space 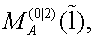 being endowed with the
-modified Poisson structure (3.15), is strongly reduced via the Dirac scheme [4,32], subject to the set
being endowed with the
-modified Poisson structure (3.15), is strongly reduced via the Dirac scheme [4,32], subject to the set 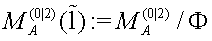 coincides with the corresponding Dirac type reduction of the
-modified Poisson structure, defined on the full phase space
As a result of simple enough yet cumbersome calculations we arrive at the following Poisson brackets
coincides with the corresponding Dirac type reduction of the
-modified Poisson structure, defined on the full phase space
As a result of simple enough yet cumbersome calculations we arrive at the following Poisson brackets 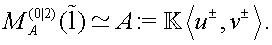
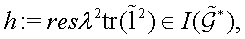 one easily obtains the following [5], nonlinear integrable Kontsevich dynamical system
one easily obtains the following [5], nonlinear integrable Kontsevich dynamical system 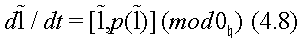
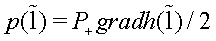
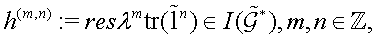 one can obtain a complete set of
-commuting to each other conservation laws of the Kontsevich dynamical system (4.7), thus proving its generalized integrability. Moreover, choosing both another group algebra and orbit elements
one can obtain a complete set of
-commuting to each other conservation laws of the Kontsevich dynamical system (4.7), thus proving its generalized integrability. Moreover, choosing both another group algebra and orbit elements 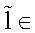 one can construct the same way many other integrable Hamiltonian systems on the associative noncommutative phase space A, that is planned to be a topic of a next investigation.
one can construct the same way many other integrable Hamiltonian systems on the associative noncommutative phase space A, that is planned to be a topic of a next investigation. This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.
 Help ?
Help ?


 Save to Mendeley
Save to Mendeley