The intracranial system: A new interpretation of the Monro-Kellie doctrine

In this paper we have reported our experience in several years in whom we have studied the phenomena correlated with the intracranial pressure. We have started to study different types of animals during an experimental condition of intracranial hypertension; we have observed many different configurations in spontaneous pathologic humans, and, eventually, in last years we have passed to confirm our ideas modelling an intracranial system in a physical phantom made by a centrifugal pump, stainless steel for base, glass for the wall, elastic tube for the cerebrovascular tree and collapsible tubes for venous drainage.

We have noted that there is some confusion about the so-called Monro-Kellie doctrine; the major part of the scientist believe in a sort of static interpretation given by the sum of the compartment which constitute the intracranial system (parenchyma, blood and cerebrospinal fluid). But we believe in a dynamic interpretation in which there is a constant balance between the arterial inflow and venous outflow during each cardiac cycle.

In this paper we have focused on the results, obtained in the different preparations, animals, humans and in vitro, all confirming the assumption that there is no difference between arterial inflow and venous outflow.

Introduction

With the term “intracranial system” we define the complex system constituted by the brain parenchyma (including the vasculature and the cerebrospinal fluid [CSF]) and its envelopes, the dura mater, and the skull. The so-called Monro-Kellie [1] doctrine states the rule to which obeys this structure, that is the absolute constancy of the intracranial volume. The presence of CSF was ignored by Monro and Kellie; their doctrine was later enunciated by Cushing in 1925 [2] and formulated as we know today as the sum of the volume of the brain plus the CSF volume plus the intracranial blood volume is constant. This conclusion was different from this stated by original doctrine of Monro and Kellie in which they affirm: “For, whilst the heart is performing its systole, the arteries here, as elsewhere, may be dilating, and in the meantime, a quantity of blood, equal to that which is dilating them, is passing out of the head by the veins” [1]. This statement confirms not a static relationship between a closed box and its content, but a dynamic approach to explain the relationship between a pulsatile and continuous perfusion and a closed, totally filled, and non-expandable case of bone [3]. This doctrine implicitly affirms that the quantity of blood coming in and out from the brain is the same and that the blood coming out from the brain must be pulsatile and synchronous with arteries, in order to maintain constant the volume of blood. This conclusion is in obvious conflict with the assumptions made by a paper [4] in which the authors propose a continuous monitoring of the Monro-Kellie doctrine. They affirm: “1) The cross-sectional area of the insonated artery remains “constant” during the cardiac cycle (Toth et al 2000); and 2) The low-pulsatile venous outflow can be written as an averaged arterial inflow (Avezaat and van Eijndhoven, 1984)”. These assumptions appear to be very extreme “simplifications” of well-established notions as enunciated firstly by Starling in 1912 [5] and demonstrated later by Aaslid in normal humans [6] and by us in pigs [7] and in craniectomized decompressed humans [8].

In this paper, with the aim of elucidating the exact temporally correlations between arterial inflow and venous outflow, we will express the observations made on these three different situations: 1) in pigs, during experimental conditions of intracranial hypertension; 2) in humans, during an intraventricular test at constant rate for the diagnosis of normal pressure hydrocephalus; 3) in a physical model of intracranial system.

The results will be compared and discuss together to obtain a more precise definition of the true significance of the Monro-Kellie doctrine.

Materials and methods

Experimental condition of intracranial hypertension in pigs

All animals used in this study were cared and used in humane fashion, complying with the guidelines established in Guide for the Care and Use of Laboratory Animals. Approval of the study protocol by the local institutional ethic committee (Catholic University School of Medicine, Rome, Italy) was obtained in 2002, before commencement of all experiments.

Six domestic female pigs weighing between 20 and 25 kg were used. The animals were anesthetized with 5 mg/kg ketamine, paralysed with 0.4 mg/kg/h pancuronium bromide, and mechanically ventilated with a gas mixture of 0.5–1% halothane, 50% N2O, and oxygen. The respiration of the animals was adjusted to yield a PaCO2 of about 35 mmHg and a PaO2 of more than 100 mmHg. No artificial system to keep a constant body temperature was used. General anaesthesia was never discontinued until the animal was killed.

Arterial Blood Pressure (ABP) was measured through a 16G catheter inserted into the right common carotid artery at the neck. After the insertion of an 18G epidural needle in the lateral ventricle, Ringer’s lactate (as mock CSF) was infused to produce intracranial hypertension up to Intracranial Pressure (ICP) mean levels approaching ABP mean levels. Mean ABP was left free to oscillate during all the experimental procedure. ICP was measured through the same 18G epidural needle used for the infusion. Two skull-windows were performed: one in the posterior part of the middle vertex at the level of the sagittal sinus and another in the left temporal bone at the level of the middle cerebral artery. Over these two windows, the blood flow velocities were measured by means of a Dual-frequency Directional Doppler (PARKS 1052) using two ultrasound continuous wave probes (8 and 4 MHz respectively). Acrylic cement was used to fix the probes and to reconstitute the integrity of the skull, to maintain the original cerebral–spinal compliance.

Anatomy of the cerebral arterial and venous system in pigs is quite like that in humans. However, whereas two separate branches form the middle cerebral artery complex, the sagittal venous sinus, like in humans, drains from cortical and bridging veins to the systemic circulation [9,10]. In this experimental preparation, it was very important for us to observe the precise temporal correlations between the blood flow velocity recorded at arterial and sinus level, without any value attributed to the real instantaneous values of flow of the two variables. For this reason, all the parameters, ABP, ICP, Mean Cerebral Artery Blood Flow Velocity (MCABFV) and Sagittal Sinus Blood Flow Velocity (SSBFV), were simultaneously recorded by means of a monitor (CMSM1167A Philips) connected, through of an analogue-to-digital converter (PCI-6024E16 analog input, 12 bit, 200 ks/s; National Instruments), with a personal computer (with Microsoft Windows XPH installed) and were automatically analysed using a self-developed software based on the Fourier frequency analysis of a single wave [11].

The aim of the experiments was to study the blood flow velocity during ICP increase, at the level of the middle cerebral arteries and sagittal venous sinus. Mock CSF was infused at a progressively increasing rate, starting from 12 ml/h, up to brain tamponade, i.e., intracranial circulatory arrest, documented by the simultaneous measurement of mean zero flow velocity at both vessel sites. Both at the arterial and sinus level, the so-called ‘reverberating wave’ was also evident.

Data acquisition was performed starting from basal level for about each 20 mmHg of ICP increments. At each step, MCABFV and SSBFV were correlated with the correspondent ICP value.

Intraventricular infusion test in normal pressure hydrocephalic patients

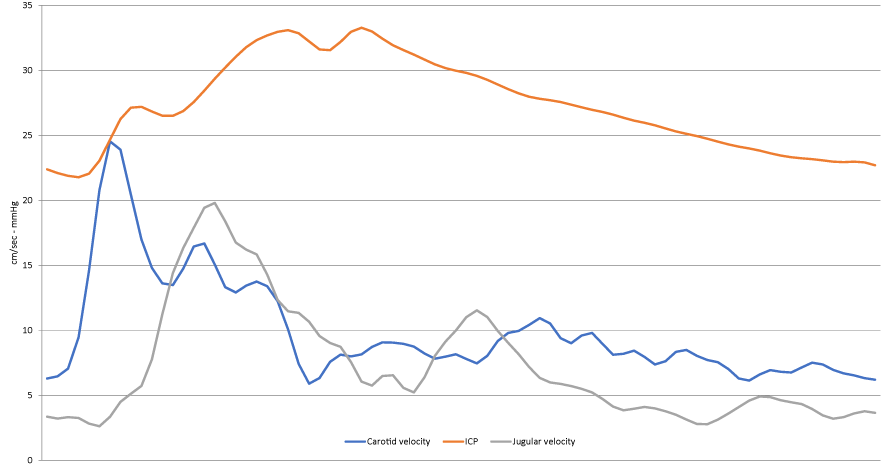
This experience was conducted, after previous informed consent as established by our Ethics Committee, during a standardized routine procedure of an intraventricular infusion test, in three patients, suspected to be affected by normal pressure hydrocephalus, with the aim to monitor the cerebral autoregulation. In these patients we have recorded, beyond the ICP, the blood flow velocity of the common carotid artery and internal jugular vein at the neck level. The test was performed infusing a Ringer lactate solution at a rate of 1 ml/min for about 20 – 30 minutes into a previously inserted ventricular catheter. ICP, Common Carotid Artery Blood Flow Velocity (CCABFV), and internal Jugular Vein Blood Flow Velocity (IJVBFV), were simultaneously monitored by the same instruments as described before and recorded by the same personal computer utilizing the same self-developed software. A particular attention was paid to look the exact temporal synchronization of the three signals in basal situations and during the test.

Physical model of intracranial system

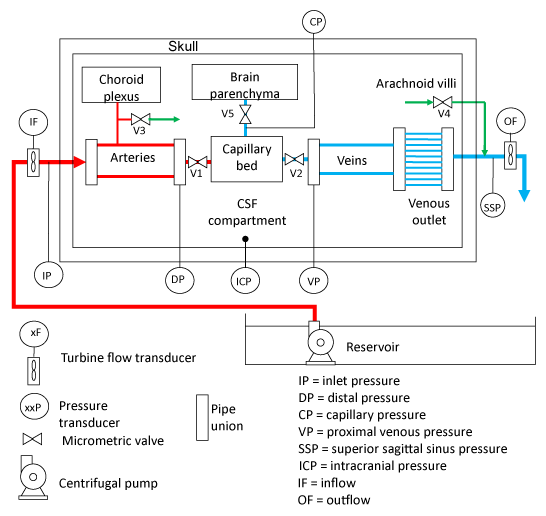
For the aim of this study, we will utilize a simplified explanation of the model of intracranial system as just published in 2018 [12]. The physical model is composed of a container that mimics the skull, which encloses the cerebrovascular, arachnoid, and ventricular systems (considered as unique CSF space) and the brain parenchyma. Fluids circulate and form the different elements: blood, CSF, and interstitial fluid. The scheme of the physical model is shown in Figure 1 (the reader is invited to follow the indications shown in the figure). The fluid, which emulates the blood, is supplied at an established pressure, that we will name Inlet Pressure (IP), by a controlled centrifugal pump, and circulates through arteries, capillaries, and veins; the fluid outflow takes place through the venous outlet in a reservoir at atmospheric pressure. Two rubber elastic tubes are employed to model the arteries; one of them is connected to a small resistance mimicking the choroid plexuses and draining into the CSF space; the venous circuit is implemented using two other tubes that split into smaller vessels (from 10 to 2), which simulate the venous outlet. These two main tubes, made by the same substance than those mimicking the arteries, have a major diameter and less thickness than those utilizing for the arteries. The valves V1 and V2 are employed to regulate the fluid flow and the pressure drops, and to emulate the effect of arterioles and venules.

Figure 1: Scheme of the hydraulic circuit.

The cranial cavity is filled with a fluid, which is produced and drained through the adjustable valves V3 and V4 that simulate the behaviour of the choroid plexuses and of the arachnoid villi, respectively. The brain parenchyma compartment, made by the viscoelastic sponges, is perfused by the interstitial fluid, supplied by the capillary bed through valve V5.

Pressures and flows are measured by several transducers. Some of them measure quantities that are not directly accessible “in vivo”, namely Distal Arterial (DA), Proximal Venous (PV) and Capillary Pressures (CP) and are here employed to tune the model and to give a deep insight on the hydraulic response of the intracranial system.

The container that emulates the skull and dura mater is cylindrical; the base is made of stainless steel; the side wall is glass; the upper lid can be removed and is Plexiglas.

The fluid that emulates the blood can be composed of demineralized water or water/glycerol solutions to better simulate blood viscosity.

The capillary bed, made by the same viscoelastic sponges of the brain parenchyma, guarantees the damping of the pulsatile component of the blood pressure jointly with a small pressure drop.

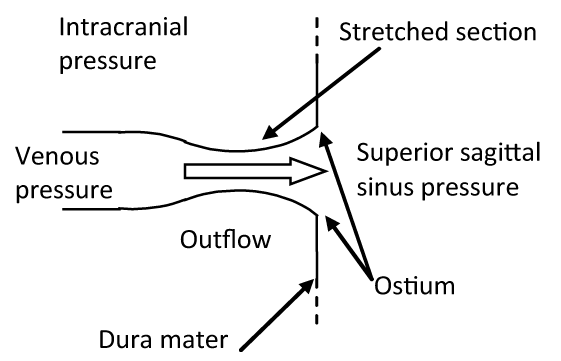
Particular attention was paid in replicating the same anatomical structure of the physiological venous outlet (Figure 2). This consists in a particular structure located at the site where the cortical veins (the so-called bridging veins) enter the dural sinuses. At this level, the “cuff-compression” of these veins determined by the ICP transmitted through the CSF flowing into the subarachnoid space reproduces a hydraulic model known as the “Starling resistor”, that is a mechanism that is able to maintain a constant flow through collapsible tubes (such as the distal parts of the veins) when the latter ones are contained in a rigid box (such as the skull). In this mechanism, the changes in the venous outflow resistance, within a precise range, are compensated by the increase in the upstream vascular pressure determined by the ICP increase [13-15]. We have replicated this mechanism utilizing a maximum of ten pipes constituted by 6 mm-width Penrose tubes connected to rigid ostium, which collapse with a negative transmural pressure of about 0.1 mmHg.

Figure 2: Scheme of the horizontal section of a cortical bridging vein.

Six Abbott Transpack® pressure sensors have been inserted to measure the different pressures: IP, DA, CP, and PV, superior Sagittal Sinus Pressure (SSP) and ICP (Figure 1). Inflow and Outflow (IF and OF) are measured by two GEMS Ft-210® turbine flow rate sensors.

A centrifugal submersible pump was chosen to supply about 10-15 cm3/sec at a pressure of about 100 mmHg. The pump velocity is controlled by an inverter. It is possible to select different velocity profiles and frequencies in the range 48-80 beats/min.

Data acquisition is performed by means of a Philips®CMS Patient Monitoring System M1167A with a sampling rate 1/128 s. To reduce the measurement noise, signals are post-processed using a third order type 2 Chebycheff low-pass filter with 30 Hz cut-off frequency. Signals are filtered forward and backward to prevent phase shift, thus preserving the original wave shape.

For the aim of this paper, we will describe specifically the measurements recorded when the container was “open” subjected to the atmospheric pressure, and when it was firmly “closed” isolated by the atmospheric pressure.

Result

Experimental condition of intracranial hypertension in pigs

As previously described [16], in basal condition, mean MCABVF ranged between 14 and 21 cm/s in all the animals; these values remained rather constant until Cerebral Perfusion Pressure (CPP), that is the difference between ABP and ICP, dropped below 70 mmHg; starting from this point, a progressively steeper decrease was evident until zero flow was reached. In the same condition, mean SSBFV ranged between 7 and 11 cm/s in all the animals; these values remained rather constant until CPP dropped below 60 mmHg; starting from this point, a progressively steeper decrease was evident until a zero flow was reached. In basal condition, pulsatile MCABVF ranged between 6 and 4 cm/s in all the animals; these values remained constant until CPP dropped below 60 mmHg; starting from this point, a progressively steeper increase was evident reaching the highest values (ranging between 18 and 12 cm/s) when mean MCABFV values approached zero. The same behaviour, but with a less evidence, was observed at level of a pulsatile SSBFV: following the decrease of CPP, also the pulsatile SSBFV showed a progressive increase reaching the maximum when the mean SSBFV reached the zero value (Figures 3,4). The two waveforms, arterial and venous waveforms, appear to be “temporally absolutely coincident” [7] at the same observation time; the difference in the absolute value depends on the different calibre of the vessel, one is smaller, the artery, the other one is larger, the sagittal sinus.

Figure 3: Example in a pig of an episode of intracranial hypertension until ICP approached ABP: The pressure waves were recorded simultaneously at different ICP values. Each wave is representative of the averaged five consecutive waves.

Figure 4: Example in a pig of an episode of intracranial hypertension until ICP approached ABP: the waves of arterial and venous (at sagittal sinus level) velocities were recorded simultaneously at different ICP values. Each wave is representative of the averaged five consecutive waves.

Intraventricular infusion test in normal pressure hydrocephalic patients

During the three infusion tests, the ICP, starting from the basal values ranging between 2 – 12 mmHg, increases until reached, in one 35 mmHg, and in the remaining two 28 mmHg. No modifications in doppler pulse wave morphology were observed, neither in CCABFV, neither in IJVBFV during the entire duration of the three tests, thus confirming the preservation of the autoregulation; they, obviously, were of different morphology, more pointed the CCABFV, more rounded the IJVBFV (Figure 5). Of particular interest was the time in which they appear in relation to the CSF pulse wave. Firstly, appears the CCABFV pulse wave, after about 40 milliseconds appears the correspondent CSF pulse wave and after a period ranging from 30 to 60 milliseconds appears the IJVBFV pulse wave; considering that the waves are recorded at neck level, while the CSF pulse wave is recorded into the skull, this means that at intracranial level the CCABFV and the IJVBFV pulse waves are “temporally absolutely coincident”.

Figure 5: An example in a man of a simultaneous recording of the two waves recorded at neck at carotid and jugular level, and the correspondent ICP wave.

Physical model of intracranial system

Neglecting other considerations for what we remind to previous paper [12], here we want to dress your attention to the appearance of the different waves of the different signals recorded in the intracranial system.

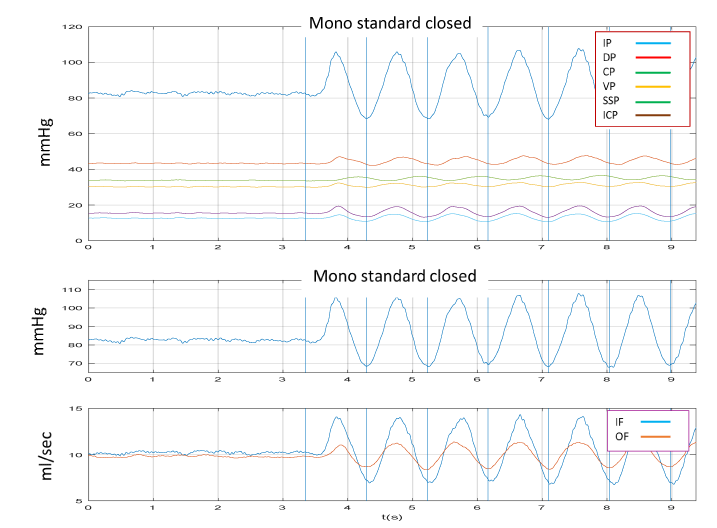
When the upper lid of the container is removed and the intracranial system is open to the atmosphere, inducing an oscillating sinusoidal periodic movement in the pump, the signals that will appear are, respectively, IP with IF, followed by DP, CP, VP, SSP and OF. In this condition, only slight oscillations of the VP have been observed; the same occurs for the SSP and the OF, which are practically constant without any visible wave (Figure 6). This sequence remains constant without any movement visible at level of the tubes simulating the Starling’ resistor during an entire cycle mimicking the systolic and the diastolic phases.

Figure 6: The simultaneous recording when the intracranial system of physical model is open: IP, DP, CP, VP, SSP and ICP are in the upper graphic; in the bottom there are two more graphics, the superior is the same IP than before, the lower graphic shows IF and OF.

When, on the contrary, the container was filled by fluid and the upper lid firmly closed, applying the same oscillation than before, IP, IF, OF, ICP, SSP, VP, will appear in the same moment, followed by DP and CP (Figure 7). In this condition a clear movement of the tubes simulating the Starling’ resistor with a systolic and diastolic phase will be evident (Figure 8). Of great interest is the datum that IF and OF are “temporally absolutely coincident”.

Figure 7: The simultaneous recording when the intracranial system of physical model is closed: IP, DP, CP, VP, SSP and ICP are in the upper graphic; in the bottom there are two more graphics, the superior is the same IP than before, the lower graphic shows IF and OF. To notice the appearance of ICP, VP, and SSP immediately in correspondence to IP; furthermore, the IF and OF are synchronous with IP.

Figure 8: The pictures show the behaviour of the last portion of tubes simulating the Starling’s resistor (in the right of the figure), in relation to the progression of sinusoidal wave (in the left of the figure) from diastolic to systolic phase. Larger in the proto-diastolic phase and narrower in the systolic phase. For better explanation, in the middle part of the figure, are shown schematic illustrations of the progression from diastolic to systolic phase (red ball).

Discussion

Of particular importance in discussing the results here reported is the absolute concordance among the three situations, animal experiment, clinical experience, and physical model, that is the “temporally absolutely coincident” between the arterial inflow and the venous outflow. This result is “unique” in the bodies of vertebrates and is determined by the existence of the intracranial system.

While the other organs constituent vertebrates’ bodies, as in the humans, have an arterial pulse inflow, which progressively becomes an almost continuous venous outflow, in the intracranial system of all the vertebrates, due to the closure of the cranium, the venous outflow becomes “pulsatile” to balance instantaneously the arterial pulsation to maintain constant the intracranial volume. This happens by the presence of CSF, which acts as mediator for this kind of movements: it transfers the arterial dilation into the external compression of the distal part of veins, the Starling resistor level. In other words, while the venous outflow in all the other parties of the body in all vertebrates depends on a physical law of pressure and flow, which are temporally correlated as happens in the physical model when the system is “open”, the venous outflow from the intracranial system depends on a mechanism due to arterial pulsation which “actively” push forward the venous blood out from the skull.

What is the meaning of this mechanism? For the moment we have two answers: the first is the possibility in a such mechanism to have a real physical support to guarantee the so-called “auto-regulation”. Indeed, the Starling resistor, for its nature in which the flow within the tube depends also on the pressure out of the tube gives the opportunity, when the pressure out of the tube, in this case the ICP, increases within a certain range, to maintain constant the flow into the tube, independently from the inlet pressure, that is the systemic pressure [15]. This theory was firstly formulated by Chopp, Portnoy and Branch in 1983 [16]; furthermore, Chopp and Portnoy, three years before [17], had reported that there was no difference between the appearance of ICP and VP, this last one measured by inserting a catheter retrogradely from the sagittal sinus into a bridging vein in the dog, thus also confirming our data.

The second answer is relative to the position of the head in the space: since the mechanism is an active mechanism modulated by the arterial pressure, this fact renders the perfusion of the brain independent from its position in the space. The blood does not flow from the brain for gravity, as happens, for instance, for the face or tongue or eyes, in which there is not Starling resistor, but flows from the brain only for the pulsatile force produced by arterial pulsation. This is the only possible explanation for the “temporally absolutely coincidence” between the arterial inflow and the venous outflow observed in these different conditions.

This is, in our opinion, the real significance of the old theory named Monro-Kellie doctrine.

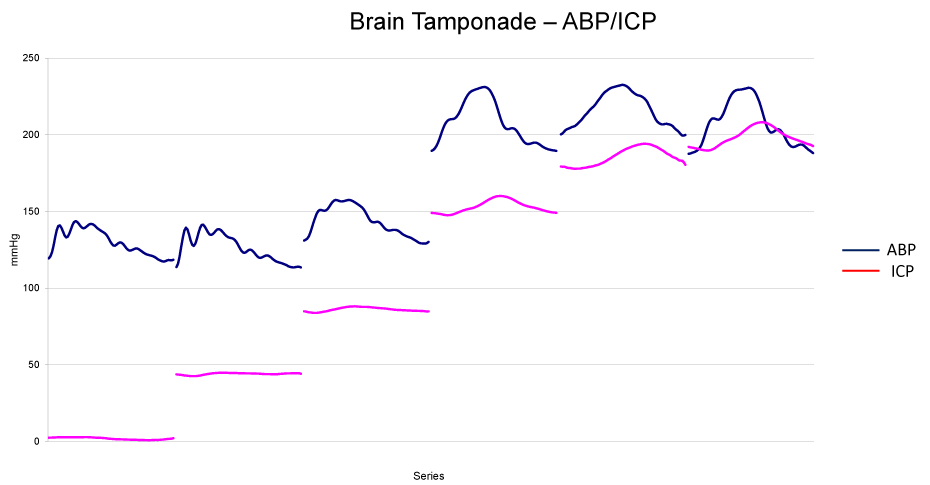
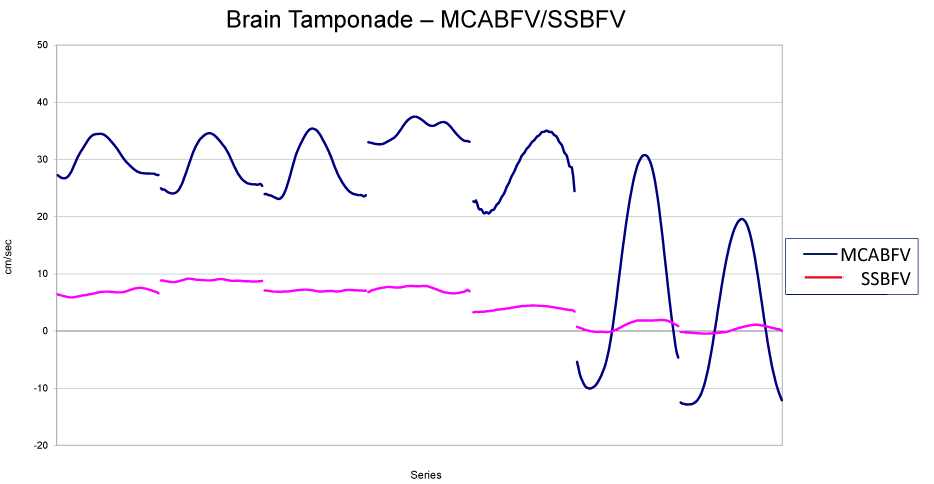
There is, unfortunately, a very dramatic consequence of this condition, and this is the so-called “brain tamponade”; this is an unusual condition in which, for a very big oedema of brain parenchyma, or for a very big increase of ICP for different causes (hematoma, brain tumour, encephalitis, other pathologies), there is no more CSF able to activate the balance mechanism between arteries and distal part of veins, the flow stops at its entrance in the carotid arteries because there is no flow coming out from the veins into the sagittal sinus [18]. This phenomenon, called brain tamponade in analogy with the cardiac tamponade, identifies a situation in which two columns of blood synchronously oscillate in a to and fro movement without any communication between each and other one.

1. Monro A (1783) Observations on the structure and functions of the nervous system: Illustrated with tables / By Alexander Monro. Edinburgh: printed for, and sold by, William Creech and Joseph Johnson, London. Link: https://bit.ly/3dn1SQv
2. Cushing H (1925) The third circulation and its channels. Lancet 2: 851-857.
3. De Bonis P, Anile C (2014) Storms, hanged pirates, anaemia, exsanguination: the contributions of Monro, Kellie and Abercrombie in understanding intracranial blood circulation. Veins and Lymphatics 3: 93-96. Link: https://bit.ly/3wXu1oR
4. Kim DJ, Czosnyka Z, Kasprowicz M, Smieleweski P, Baledent O, et al. (2012) Continuous Monitoring of the Monro-Kellie Doctrine: Is It Possible? J Neurotrauma 29: 1354-1363. Link: https://bit.ly/3swq5YZ
5. Starling EH (1912) Principles of human physiology. Link: https://bit.ly/3aiFUfg
6. Aaslid R, Newell DW, Stooss R, Sorteberg W, Lindegaard KF (1991) Assessment of cerebral autoregulation dynamics from simultaneous arterial and venous transcranial Doppler recordings in humans. Stroke 22: 1148-1154. Link: https://bit.ly/32lCpAC
7. Anile C, Ficola A, Fravolini ML, La Cava M, Maira G, et al. (2002) ICP and CBF Regulation: A new Hypothesis to Explain the “Windkessel” Phenomenon. Acta Neurochir 81: 113-116. Link: https://bit.ly/3tuiOKw
8. Anile C, Ficola A, Fravolini ML, La Cava M, Maira G, et al. (2002) ICP and CBF Regulation: Effect of the Decompressive Craniectomy. Acta Neurochir 81: 109-111. Link: https://bit.ly/2RH5wMz
9. Fries G, Wallenfang T, Hennen J, Velthaus M, Heimann A, et al. (1999) Occlusion of the pig superior sagittal sinus, bridging and cortical veins: multistep evolution of sinus-vein thrombosis. J Neurosurg. 77: 127–133. Link: https://bit.ly/2OS1FLt
10. Imai H, Konno K, Nakamura M, Shimizu T, Kubota C, et al. (2006) A new model of focal cerebral ischemia in the miniature pig. J Neurosurg 104: 123-132. Link: https://bit.ly/3doIGSe
11. Anile C, De Bonis P, Albanese A, Di Chirico A, Mangiola A, et al. (2010) Selection of patients with idiopathic normal pressure hydrocephalus for shunt placement: a single-institution experience. J Neurosurg 113: 64-73. Link: https://bit.ly/3x8Fm5N
12. Ficola A, Fravolini ML, Anile C (2018) A Physical Model of the Intracranial System for the Study of the Mechanisms of the Cerebral Blood Flow Autoregulation. IEEE Access 6: 67166-67174. Link: https://bit.ly/2Qr7Ruo
13. Vignes JR, Dagain A, Guérin J, Liguoro D (2007) A hypothesis of cerebral venous system based on a study of the junction between the cortical bridging veins and the superior sagittal sinus. J Neurosurg 107: 1205-1210. Link: https://bit.ly/32jbLrR
14. Nakagawa Y, Tsuru M, Yada K (1974) Site and mechanism for compression of the venous system during experimental intracranial hypertension. J Neurosurg 41: 427–434. Link: https://bit.ly/3tn5BDa
15. Anile C, De Bonis P, Di Chirico A, Ficola A, Mangiola A, et al. (2009) Cerebral blood flow autoregulation during intracranial hypertension: a simple, purely hydraulic mechanism? Childs Nerv Syst 25: 325-335. Link: https://bit.ly/3e03Jti
16. Chopp M, Portnoy HD, Branch C (1983) Hydraulic model of the cerebrovascular bed: an aid to understanding the volume-pressure test. Neurosurgery 13: 5-11. Link: https://bit.ly/3uZoht5
17. Chopp M, Portnoy HD (1980) System analysis of intracranial pressure: comparison with volume-pressure test and cerebrospinal fluid pulse amplitude analysis. J Neurosurg 53: 516-527. Link: https://bit.ly/32hpAXZ
18. Anile C, De Bonis P, Fernandez E, Ficola A, Petrella G, et al. (2012) Blood flow velocities during experimental intracranial hypertension in pigs. Neurol Res 34: 859-863. Link: https://bit.ly/3slvIZB